The Financial Journal is a blog for all financial industry professionals. This blog has been, and always will be, interactive, intellectually stimulating, and open platform for all readers.
AdSense
Sunday, April 30, 2017
Essential problem
If you want to figure out what an essential problem is, you have to be objective and see things from a higher perspective. Going deeper and focusing on details do not necessarily bring you to the essential problem.
Friday, April 28, 2017
"The best way to predict the future is to invent it." Alan Kay
"The best way to predict the future is to invent it."
Alan Kay
"The best way to bet on the future is to invest in it."
An anonymous investor
Alan Kay
"The best way to bet on the future is to invest in it."
An anonymous investor
Good Sleep
Chapter 2 Routines for a good night sleep
(1) make a light dark 2 hours before sleeping
(2) avoid (especially regular) noises even a fridge or a clock - earplug or snow music in small volume would also be ok
(3) your favorite slow music with regular tempo in small volume
(4) aroma - lavender, camomile, sandalwood, clary sage, sweet orange
(5) your best bed and pillow
(6) timer setting (e.g, air conditioner) - switch off in 1-3 hours after falling asleep
(7) no food and drink 3 hours before sleeping
(8) foods for a good sleep - lettuce, onion, natto (fermented soy beans, Japanese food); have enough breakfast, lunch, and then a light meal for dinner
(9) No smartphone, PC/Mac, TV, 3 hours before sleeping
(10) Take a bath / shower with 40 centigrade; decrease an inside temperature of your body. It if it's too hot (e.g., 42 centigrade), it prevents you from having a good sleep.
(11) Do an exercise; it should be light, not strong.
(12) Perform your personal ritual. It is a self-suggestion to make you sleep.
(13) Recall good things today and prep for tomorrow, to-do and schedule, clothes and things to bring, when to get up.
(14) Sex
(15) Give up something unnecessary to have enough time for sleep. Give up one of many hobbies, drinking, etc.
(16) Rhythm and routine of your life are important; medicine could be of your help, but it is only for temporary.
Chapter 3 How to be an early bird
Waking-up-refreshed techniques:
(1) Reset your internal clock by sunlight
(2) Set a reason to get up, like jogging in the morning
(3) Have a sugar content just after getting up, such as, bananas, cookies, chocolates, or orange juice
(4) Chew gum after getting up
(5) Take a shower or wash your face
(6) Have breakfast, especially carbohydrates(e.g., rice/bread) and protein. After 2 hours of your breakfast, glucose is delivered to your brain.
(7) Caffeine, e.g., green tea (gyokuro) in the best, then black tea, coffee, or other green tea
Chapter 4 Common Sense in Sleep
Sleep too long is not good because only 2-3 hours sleep at the beginning is deep (non-REM). If you sleep longer than necessary, you have more shallow sleep.
Non-REM: brain - rest, body - relaxed and unstable (e.g., blood pressure)
REM: brain - awake, body - tense and steady
Each person has his or her own best sleeping time. Some people sleep longer while others sleep shorter.
Drinking coffee and then having a nap for 15-20 min is good; if it's longer than that, you enter a deep sleep and have trouble getting up.
Dreaming a nightmare means the quality of your sleep gets worse.
Chapter 5 Those who cannot get up in the morning - ten common points
(1) lack of sleep
(2) bad lifestyle habit
(3) biological clock - out of order
(4) too much tenseness
(5) escape from reality
(6) depressive tendency
(7) suffocation
(8) too much sleep
(9) female hormone
(10) sleepy during the day
Chapter 6 How to get up refreshed
See above.
(1) make a light dark 2 hours before sleeping
(2) avoid (especially regular) noises even a fridge or a clock - earplug or snow music in small volume would also be ok
(3) your favorite slow music with regular tempo in small volume
(4) aroma - lavender, camomile, sandalwood, clary sage, sweet orange
(5) your best bed and pillow
(6) timer setting (e.g, air conditioner) - switch off in 1-3 hours after falling asleep
(7) no food and drink 3 hours before sleeping
(8) foods for a good sleep - lettuce, onion, natto (fermented soy beans, Japanese food); have enough breakfast, lunch, and then a light meal for dinner
(9) No smartphone, PC/Mac, TV, 3 hours before sleeping
(10) Take a bath / shower with 40 centigrade; decrease an inside temperature of your body. It if it's too hot (e.g., 42 centigrade), it prevents you from having a good sleep.
(11) Do an exercise; it should be light, not strong.
(12) Perform your personal ritual. It is a self-suggestion to make you sleep.
(13) Recall good things today and prep for tomorrow, to-do and schedule, clothes and things to bring, when to get up.
(14) Sex
(15) Give up something unnecessary to have enough time for sleep. Give up one of many hobbies, drinking, etc.
(16) Rhythm and routine of your life are important; medicine could be of your help, but it is only for temporary.
Chapter 3 How to be an early bird
Waking-up-refreshed techniques:
(1) Reset your internal clock by sunlight
(2) Set a reason to get up, like jogging in the morning
(3) Have a sugar content just after getting up, such as, bananas, cookies, chocolates, or orange juice
(4) Chew gum after getting up
(5) Take a shower or wash your face
(6) Have breakfast, especially carbohydrates(e.g., rice/bread) and protein. After 2 hours of your breakfast, glucose is delivered to your brain.
(7) Caffeine, e.g., green tea (gyokuro) in the best, then black tea, coffee, or other green tea
Chapter 4 Common Sense in Sleep
Sleep too long is not good because only 2-3 hours sleep at the beginning is deep (non-REM). If you sleep longer than necessary, you have more shallow sleep.
Non-REM: brain - rest, body - relaxed and unstable (e.g., blood pressure)
REM: brain - awake, body - tense and steady
Each person has his or her own best sleeping time. Some people sleep longer while others sleep shorter.
Drinking coffee and then having a nap for 15-20 min is good; if it's longer than that, you enter a deep sleep and have trouble getting up.
Dreaming a nightmare means the quality of your sleep gets worse.
Chapter 5 Those who cannot get up in the morning - ten common points
(1) lack of sleep
(2) bad lifestyle habit
(3) biological clock - out of order
(4) too much tenseness
(5) escape from reality
(6) depressive tendency
(7) suffocation
(8) too much sleep
(9) female hormone
(10) sleepy during the day
Chapter 6 How to get up refreshed
See above.
Thursday, April 27, 2017
AI
Chapter 1 Why AI now?
Three types of AI:
(1) rule-based
(2) probability/statistics-based in Bayesian network
(3) deep learning in neural network
Current web search by Google is based on the page rank algorithm, which highly valuate a website with many links from others; many links mean that the web site is more trustworthy.
The next phases of web search are:
(1) semantic search by Google, which understands what people really want, not just search based only on a keyword used
(2) Siri, an intelligent personal assistant and knowledge navigator, by Apple
(3) graph search by FaceBook - e.g., "What is my friend's favorite song?"
Each player tries to provide necessary info after listening to what a user says; i.e., each company wants to dominate a gateway to the mobile internet.
Big data consists of:
(1) structured data (e.g., customer name, sales figures)
(2) unstructured data (irregular data like inquiries to a call center)
Chapter 2 What is intelligence?
Artificial Intelligence (AI): technology that substitutes humans' intelligent activities with machines such as computers and softwares on it
Chapter 3 Value of Intelligence
Requirements for a project:
(1) What is it for? The more a goal is concrete, the higher the probability of success is.
(2) Feasibility. Is technology developed enough to make it happen? How about human resources?
(3) Is it meaningful for a society?
(4) Why now? Is it timely?
(5) Evolvability / expansibility. What kind of technology is derived from it?
(6) Publicity. Is it interesting for a society?
(7) Motivation. Does a project motivate people?
Chapter 4 Issues of AI
(1) Risks of when people are too dependent on machines / systems.
(2) Concerns for people's employment and existence value replaced by AI.
(1) Risks of when people are too dependent on machines / systems.
Automated driving
Flash crash in stock markets
(2) Concerns for people's employment and existence value replaced by AI.
AI for chess,etc.
(1) game tree exploration (forecasting)
(2) current status / condition analysis by evaluation function
Also, AI does not get tired, feel a fear or sleepy, and lose concentration.
Friday, April 21, 2017
Originals by Adam Grant
In this book, originality is (1) opposite of conformity, homogeneity, and (2) the combination of creativity and implementation, i.e., realizing an idea that is acceptable for others.
Competitive strategy in one sentence is "doing good things for clients/customers while being different from peers in the long term." It all boils down to building barriers to imitation. Furthermore, to avoid imitations, having irrational parts that would make the whole structure rational.
Competitive strategy in one sentence is "doing good things for clients/customers while being different from peers in the long term." It all boils down to building barriers to imitation. Furthermore, to avoid imitations, having irrational parts that would make the whole structure rational.
Part 1 Creative Disruption
Do not use what we have as it is; look for better alternatives by yourself.
Justifying and maintaining a current system makes people feel relieved; if the world is what it should be, then you do not need to feel distracted by it.
However, if you reluctantly just follow something, you're losing an appropriate anger for injustice and positive attitude and willpower to make the world better.
If you're curious about an existing system that you don't agree with, you'll notice that the majority of them is due to social reasons; rules and systems are built by people. Therefore, they can be changed by people. If you realize it, then you can be brave enough to think and act to change the world.
If you have too strong will to achieve a good result, originality and/or creativity could not be the first priority. If being successful is important, then you worry about a failure. You only make an effort to achieve something that seem to be achievable.
It is likely that a company founded by people who are risk-averse and concerned about the possibility of idea to be realized could survive.
A company by a reckless gambler is more vulnerable.
When people take a risk in a certain field, people tend to behave carefully in other fields to mitigate the high risk and have optimized overall risk.
Moreover, if you are safe in a certain field, you have freedom to pursue your originality in another field.
According to some research results, entrepreneurs are not necessarily risk-seeking; actually, they are risk-averse.
Your limit is set by yourself.
People regret what they did not do rather than failing.
Part 2 Think boldly, work out finely
The biggest hurdle for original ideas is not coming up with them, but selecting them; a creator him/herself cannot evaluate their ideas appropriately.
What should we do? Come up with as many ideas as possible. According to a research, a genius creator in a certain field is not necessarily better than others in the same field, from the quality of creations. However, the more you create, the more diversified your creations will be, and it is likely to create your original works.
If you want someone to evaluate your original ideas, one of the best persons to ask is a peer in your field, not your boss / management.
If you have a variety of experience in various fields and an interest in art like dance, novels, paring, playing music, then you tend not to doubt about new and odd ideas.
When can you trust your intuition? If you (1) lack of experience, (2) are overconfident, and (3) are too passionate, it is NOT right time to believe your six-sense.
Your tuition is likely to be right in a field where you have plenty of experience, thanks to unconscious pattern recognition. On the contrary, when you lack of knowledge / experience, you should take time to analyze before making a decision.
Your invented product and/or service have/has to be not only new, but also practical.
You can rely on your intuition in a field where you have a lot of experience to make decisions for something that can be forecastable.
Things change quickly nowadays and our future is more unpredictable than before. We cannot rely on intuition and experience to support when we try new things; therefore, analyses are more important.
If you were successful in a certain field in the past, you could be struggling in a new field; overconfidence makes you reluctant to listen to others.
If you want to choose a great idea, you should not see whether or not people with an idea succeeded, rather, "how" people became successful is important.
Part 3 Change Indifference to Passion - how to get people around you involved
The great has always been facing opposing views.
When someone is trying hard to make things better but people around him/her don't respect him/her, this person could be caught in a vicious circle of a grudge. This person tries to show how important he/she is, and behave in a pompous manner.
Specificity Credit:
If someone behaves in a way that people don't expect, this person could be regarded as one with higher ability and status; since he or she is special, he/she can behave abnormally.
If you admit your (company's) weakness, then you have four merits:
1. Audience let their guard down. People try not to be sold.
2. Pessimists look smart and excellent in insight.
3. You look trustworthy.
4. People think something important when they can recall it easily; if you show negative things to your audience first, the audience find coming up with more negative things hard. Moreover, if the audience quickly figure out positive factors, that would be even better.
Mere Exposure Effect:
The more you have an exposure to something / someone, the better you like it / the person. This is applicable when you tell your new idea to others; repeatedly tell them.
When you are not satisfied with a current status, there are four ways to deal with it.
x-axis: benefit or damage to an organization
y-axis: change or do not change the current status
Action (x, y)
1. Separation / Withdrawal (damage, change)
2. Say your opinion (benefit, change)
3. Persistence (benefit, do not change)
4. Ignorance (damage, do not change)
A way you choose depends on (1) your controllability of the situation and (2) your commitment to the situation. That is, whether or not you believe you can change and you have a strong interest to change the situation.
If (1) you cannot change and (2) you do not have a commitment(interest), then your choice would be 4. Ignorance.
If (1) you cannot change but (2) you have a commitment, then your choice would be 3. Persistence.
If (1) you can change but (2) you do not have a commitment, then your choice would be 1. Separation.
If (1) you can change and (2) you have a commitment, then your choice would be 2. Say your opinion.
If someone is in the middle class, he/she tends to go along with others; they are in an unstable status and do not want to risk their position. They want climb up, but they also worried about losing and falling off.
Someone in the lower class do not have many things to lose; rather, they gain a lot if they stick to their original ideas.
Someone in the upper class is regarded as a different person and is expected to behave differently.
When you try to change something, then it is efficient to talk to the upper and lower class and avoids talking with the middle class. (An exception could be a politician under democratic systems).
What we can do is say your opinion while keeping your risk portfolio (status) safe and prepare for a possibility to leave your current working place.
In the long run, people regret a failure because of what they didn't do, not what they did.
Part 4 The wise wait for the right time and the fool rushes.
Procrastination (delaying something) might be bad from a productivity point of view, but might be a source of a creativity if you have a passion to generate a new idea and keep trying more possibilities and improving.
Being original has to be different from, and better than, others.
Moving first does not necessarily mean you have a high probability to be successful. If a market is unstable, uncertain, or pioneered, than the first could be disadvantaged. If you have an original idea, then it is not always right to rush and get to a goal faster than others. (Exceptions could be something related to patents or network effect like telephone and social networking services.)
There are two types of innovations.
- Conceptual innovation (backed by a great and brand-new idea, not affected by experience, done by a sprinter)
- Experimental innovation (backed by trial and error, and experience, done by a marathon runner)
Part 5 Who You Work with Determines Winning or Losing
When working with a group of people who have a similar sense of value, it is important to have a common way of doing things to sympathize.
The originals have to be a moderate extremist to be successful. They have untraditional ideas but persuade people in a mainstream. Focusing on how, not why, could mitigate the degree of the extremeness.
(positive effect, negative effect)
(Low, Low) acquaintance who has almost no interest
(High, Low) friends who are always supportive
(Low, High) enemies who always try to interrupt
(High, High) "frienemies" who both support and interrupt
The best approach is to change your enemies to your supporters. The best supporters are someone who were against you, but are now for you.
You tend to appreciate someone who are gradually supportive more than others who are always supportive. If you start to like those who were against you, they also begin to like you. They try to avoid cognitive errors by making an effort to keep liking you.
Most importantly, the previously-anti-you people are the best persons to understand and persuade currently-anti-you people.
One of the most promising ideas is something you begin with an odd, untraditional things, but then add familiar, traditional things to make it persuasive, familiar, and popular.
It is very hard to change others' value; it is much easier to find common factors of your and their values, and connect them.
Part 6 The misfit, who is out of line, goes ahead of the times.
Many of the original are risk takers because people around them respect their independence and protect them.
When parenting, if parents explain children that they believe their children can understand, grow, and improve, children tend to consider their behaviors and effects on others by that. Those parents also tell their children that children should make their own rules by themselves. On the contrary, some parents force children to follow their (parents') rules.
When thinking about yourself, a logic of results works. When thinking about others, a logic of validity works; a man/woman like me should do what under this circumstance?
If you appreciate someone's personality, not deed itself, he or she tends to take it as a part of his or her identity. He or she doesn't think that he/she just behaves appropriately; he or she thinks that he/she is a good person.
Part 7 Organizations get ruined, organizations get elevated
When an industry moves dynamically, a large company with a strong corporate culture in the industry gets isolated. It neither learns nor adapts, so it underperforms compared to peers and gets unstable.
If you want to build a strong culture as Bridgewater Associates by Ray Dalio does, not cult, one of the core values is "diversity". Welcoming differences in opinions is differentiating a strong culture and a mere cult. A quality of an idea matters, not a seniority, a length of career or title at a company. At Bridgewater, only the best idea is employed.
Those who cannot disagree with others in a constructive manner bring the worst tragedies to humans.
Bosses usually want their subordinates to bring solutions, not problems. However, if a company culture focuses too much on solutions, it is biased to a culture of defense and discourages the spirit of exploration. If someone is always required to show a solution, he/she has to come to a conclusion in advance, and he/she misses a chance to view and learn from a wider perspective.
If each of members in a group has different information, a leader has to clarify what the true problem is, before finding a solution and trying to defend it.
A leader is expected to find a person who disagrees with him or her in order to properly raise an issue.
Ray Dalio wants his team to bring up an issue, not necessarily a solution.
Deciding on a democratic manner, one person one vote, is foolish. Credibility of each person is not the same, says Ray Dalio.
Discuss as if you're right, listen to others as if you're wrong.
Ray Dalio thinks that the most important thing is "think by yourself."
A more powerful way than discussions for resolution of differences of opinions is science, including experiment and data collection, rather than your own logic, experience, intuition, or conversation.
An influential person has the following features:
(1) strong passion
(2) imagination
(3) intense curiosity
(4) non-conformity
(5) being rebellious
Again, "think by yourself."
Part 8 Make anything your source of energy
There are two strategies to deal with difficulties:
(A) strategic optimism
(B) defensive pessimism
If you have a strong will and a fear, then (B) is the right choice.
To overcome a fear, getting excited is better than calming down. It is easier to replace the fear with other feeling, like excitement, than to try to control the strong feeling of the fear.
On the contrary, if you do not have an enough will to take an action, it is risky to be pessimistic.
If you are ready to take an action, you should face the fears with defensive pessimism. Your "GO" system works, not "STOP" system.
To realize you are not alone, you don't necessarily have many supporters; actually, only one supporter could be enough.
Humors work when people fear - not braking by "STOP" sytems, but accelerating by "GO" systems. It's a great way for people without a power to change strong negatigve feelings to the positive ones.
Daniel Kahneman's behavial finance theory:
For a certain profit, people tend to be risk-averse; for a certain loss, people incline to be risk-seeking.
If you get angry with others, that would nurse your wrath; if you get angry "for" others, it would be an incentive to establish justice and build a better system. You don't want to punish others; you want to help people.
Being original is not an easy way to be happy; however, happiness by pursuing is not replaceable.
Amazon.com
Amazon.co.jp
Monday, April 17, 2017
Political Scholars Dillemma
Some political scholars say "I don't understand why the public supports the current administration that I think terrible."
There are some possibilities:
(A) The administration is actually terrible, and the political scholars' ideology is actually great or at least better.
The problem is that no one takes care of the political scholars. In that case, they should design and build a system to tell their ideology and doable policies to people.
(B) The administration is actually terrible, but the political scholars' ideology is much worse.
It is hard for the scholars to admit they are idiots.
(C) The administration is actually great, and the political scholars' ideology is much better.
It is natural for people to maintain the status quo. Also, the scholars have to prove that they are trustworthy.
(D) The administration is actually great, and the political scholars' ideology is worse.
Saying "both the administration and the public are fool" might make the scholars feel relieved; after all, the scholars have an incentive to believe that the administration and the public don't know what the scholars know.
Sunday, April 16, 2017
Deep Learning with Python from scratch (for image recognition, neither natural language nor sound)
[0] Prep
For programs used in this article, visit the following website > Clone or download > Download ZIP
https://github.com/oreilly-japan/deep-learning-from-scratch
Anaconda distribution for data analysis, which includes NumPy (numerical calculation) and Matplotlib (graph drawing)
https://www.continuum.io/downloads
Choose Python 3.X for your platform (in my case, Mac OS)
Install the downloaded pkg file.
After the installation, open Terminal on Mac OS (or cmd on Windows) and enter the following code:
$ python --version
Python 3.6.0 :: Anaconda 4.3.1 (x86_64)
This shows you that the installation has been successfully ended.
Start the Python interpreter:
$ python
Python 3.6.0 |Anaconda 4.3.1 (x86_64)| (default, Dec 23 2016, 13:19:00)
[GCC 4.2.1 Compatible Apple LLVM 6.0 (clang-600.0.57)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>>
[1] Intro
[1.3.1] Numerical Calculation
>>> 1 + 2
3
>>> 1 - 2
-1
>>> 4 * 5
20
>>> 7 / 5
1.4
>>> 3 ** 2
9
[1.3.2] Data Type
>>> type(10)
<class 'int'>
>>> type(2.718)
<class 'float'>
>>> type("Hello")
<class 'str'>
[1.3.3] Variable
>>> x = 10 #initialization
>>> print(x)
10
>>> x = 100 # substitute
>>> print(x)
100
>>> y = 3.14
>>> x * y
314.0
>>> type(x * y)
<class 'float'>
[1.3.4] List
>>> a = [1, 2, 3, 4, 5] # create a list
>>> print(a)
[1, 2, 3, 4, 5]
>>> type(a)
<class 'list'>
>>> len(a)
5
>>> a[0] # access the first element
1
>>> a[4] # access the last (fifth) element
5
>>> a[4] = 99 # substitute the last (fifth) element with 99
>>> print(a)
[1, 2, 3, 4, 99]
>>> a[0:2] # Show 1st (0) and 2nd (1) elements, but not 3rd (2) elements.
[1, 2]
>>> a[1:] # Show elements from the second (1) to the last.
[2, 3, 4, 99]
>>> a[:3] # Show elements from the first (0) to the third (2); the fourth(3) is NOT included.
[1, 2, 3]
>>> a[:-1] # Show elements from the first (0) to the last minus 1 (fourth, 3).
[1, 2, 3, 4]
>>> a[:-2] # Show elements from the first (0) to the last minus 2 (third, 2).
[1, 2, 3]
[1.3.5] Dictionary
>>> me = {'height':180} # Create a dictionary.
>>> me['height'] # Access an element of the dictionary.
180
>>> me['weight'] = 70 # Add a new element to the dictionary.
>>> print(me)
{'height': 180, 'weight': 70}
[1.3.6] Boolean
>>> hungry = True
>>> sleepy = False
>>> type(hungry)
<class 'bool'>
>>> not hungry # not True, i.e., False
False
>>> hungry and sleepy # True and False, i.e., False
False
>>> hungry or sleepy # True or False, i.e., True
True
[1.3.7] if
>>> hungry = True
>>> if hungry:
... print("I'm hungry.") # You have to put at least single space (ideally four spaces) after if
...
I'm hungry.
>>> hungry = False
>>> if hungry:
... print("I'm hungry") # You have to put at least single space (ideally four spaces) after if
... else:
... print("I'm not hungry.")
... print("I'm sleepy.")
...
I'm not hungry.
I'm sleepy.
[1.3.8] for
>>> for i in [1, 2, 3]:
... print(i) # four spaces on the left hand side
...
1
2
3
[1.3.9] Function
>>> def hello():
... print("Hello, World!") # four spaces on the left hand side
...
>>> hello()
Hello, World!
>>> def hello(object):
... print("Hello, " + object + "!") # four spaces on the left hand side
...
>>> hello("everyone")
Hello, everyone!
To finish the Python interpreter, Ctrl-D for Mac OS and Linux, Ctrl-Z and Enter for Windows.
[1.4] Python script file
[1.4.1] Saving a new Python script file
Create a new file hungry.py that only includes the following line:
print("I'm hungry!")
Open Terminal on Mac OS (or cmd on Windows) and then move to the directory where you saved the file hungry.py.
$ pwd # check your present working directory
$ cd # Change directory to the directory where you saved the file hungry.py. You need to put absolute or relative path after "cd" command.
$ python hungry.py
I'm hungry!
[1.4.2] Class
In [1.3.2] Data Type, you see data types like int or str, which are checked by a built-in function, type(). You can define a new class and data type.
Create a man.py which includes the following codes:
class Man: # a new class name
def __init__(self, name): # __init___ is a special method. It is also a constructor, for initialization, which is called once when an instance of the class is created
self.name = name # self is an instance of itself. self.(attribution name) is to create an instance and access it.
print("Initialized!")
def hello(self):
print("Hello " + self.name + "!")
def goodbye(self):
print("Good-bye " + self.name + "!")
m = Man("David") # m is an instance (object)
m.hello()
m.goodbye()
On your Terminal on Mac OS (or cmd on Windows), run as follows:
$ python man.py
Initialized!
Hello David!
Good-bye David!
[1.5] NumPy
In implementations of Deep Learning, there are many calculations of arrays and matrices. Numpy array class (numpy.array) has convenient methods that can be used for deep learning implementations.
[1.5.1] Importing NumPy
On your Terminal on Mac OS (or cmd on Windows), run as follows:
$ python
Python 3.6.0 |Anaconda 4.3.1 (x86_64)| (default, Dec 23 2016, 13:19:00)
[GCC 4.2.1 Compatible Apple LLVM 6.0 (clang-600.0.57)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>>
>>> import numpy as np # import numpy libraries; from now on, you can refer to numpy methods np.*
[1.5.2] NumPy array
np.array() receives a Python list and creates a NumPy array (numpy.ndarray).
>>> x = np.array([1.0, 2.0, 3.0])
>>> print(x)
[ 1. 2. 3.]
>>> type(x)
<class 'numpy.ndarray'>
[1.5.3] NumPy mathematical calculation
Example of element-wise calculation:
>>> x = np.array([1.0, 2.0, 3.0])
>>> y = np.array([2.0, 4.0, 6.0])
>>> x + y # addition in each element
array([ 3., 6., 9.])
>>> x - y # subtraction in each element
array([-1., -2., -3.])
>>> x * y # element-wise product
array([ 2., 8., 18.])
>>> x / y # element-wise division
array([ 0.5, 0.5, 0.5])
It should be noted that number of elements in x and y are the same. If not, it causes an error.
NumPy array and single scalar calculation (broadcast):
>>> x = np.array([1.0, 2.0, 3.0])
>>> x / 2.0
array([ 0.5, 1. , 1.5])
[1.5.4] NumPy N-dimension array
>>> A = np.array([[1, 2], [3,4]])
>>> print(A)
[[1 2]
[3 4]]
>>> A.shape #
(2, 2)
>>> A.dtype
dtype('int64')
>>> AA = np.array([[1, 2], [3,4], [5,6]])
>>> AA.shape # (# of row, # of column)
(3, 2)
>>> print(AA)
[[1 2]
[3 4]
[5 6]]
>>> print(A)
[[1 2]
[3 4]]
>>> B = np.array([[3, 0], [0, 6]])
>>> A + B
array([[ 4, 2],
[ 3, 10]])
>>> A * B # not a matrix calculation, just a element-wise calculation
array([[ 3, 0],
[ 0, 24]])
>>> print(A)
[[1 2]
[3 4]]
>>> A * 10
array([[10, 20],
[30, 40]])
[1.5.5] Broadcast
>>> A = np.array([[1, 2], [3,4]])
>>> B = np.array([10, 20])
>>> A * B # element-wise calculation by broadcast
array([[10, 40],
[30, 80]])
[1.5.6] Element-wise Access
>>> X = np.array([[51, 55], [14, 19], [0, 4]])
>>> print(X)
[[51 55]
[14 19]
[ 0 4]]
>>> X[0]
array([51, 55])
>>> X[0][0]
51
>>> X[0][1]
55
[1.6] Matplotlib
Matplotlib is a library for drawing graphs.
[1.6.1] Drawing a simple graph
>>> import numpy as np
>>> import matplotlib.pyplot as plt # module pyplot for drawing graphs
>>> x = np.arange(0, 6, 0.1) # from 0 to 6, with increments by 0.1
>>> x
array([ 0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ,
1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2. , 2.1,
2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3. , 3.1, 3.2,
3.3, 3.4, 3.5, 3.6, 3.7, 3.8, 3.9, 4. , 4.1, 4.2, 4.3,
4.4, 4.5, 4.6, 4.7, 4.8, 4.9, 5. , 5.1, 5.2, 5.3, 5.4,
5.5, 5.6, 5.7, 5.8, 5.9])
>>> y = np.sin(x)
>>> plt.plot(x, y)
[<matplotlib.lines.Line2D object at 0x11d552160>]
>>> plt.show()
Ctrl-Z brings you back to Terminal on Mac OS. If you do, then run the following command to get back to Python:
$ python
[1.6.2] pyplot
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> x = np.arange(0, 6, 0.1)
>>> y1 = np.sin(x)
>>> y2 = np.cos(x)
>>>
>>> plt.plot(x, y1, label="sin")
[<matplotlib.lines.Line2D object at 0x11671a550>]
>>> plt.plot(x, y2, linestyle = "--", label="cos")
[<matplotlib.lines.Line2D object at 0x10cd3afd0>]
>>> plt.xlabel("x")
<matplotlib.text.Text object at 0x113b239e8>
>>> plt.ylabel("y")
<matplotlib.text.Text object at 0x1166d60b8>
>>> plt.title('sin & cos')
<matplotlib.text.Text object at 0x1166dd748>
>>> plt.legend()
<matplotlib.legend.Legend object at 0x11671a748>
>>> plt.show()
Ctrl-Z brings you back to Terminal on Mac OS. If you do, then run the following command to get back to Python:
$ python
[1.6.3] Show pictures
>>> import matplotlib.pyplot as plt
>>> from matplotlib.image import imread
>>>
>>> img = imread('figure_1.png') # specify a file name (or path) to your image file
>>> plt.imshow(img)
<matplotlib.image.AxesImage object at 0x11cd8a470>
>>> plt.show()
[1.7] Summary
[2] Perceptron
A perceptron is an algorithm which is an origin of neural network (deep learning).
[2.1] Perceptron
A perceptron (technically artificial neuron or simple perceptron) receives several signals as inputs and returns one output. Signals of a perception are either 0 (a signal is NOT delivered to the next) or 1 (a signal is delivered to the next).
For instance,
x1: input signal 1
x2: input signal 2
w1: weight of the signal 1
w2: weight of the signal 2
y: this receives w1x1 and w2x2
x1, x2, and y are called neurons or nodes.
(2.1)
y = 0 (w1x1 + w2x2 <= θ)
y = 1 (w1x1 + w2x2 > θ)
θ is a threshold. When the sum of received numbers (w1x1 + w2x2) is larger than the threshold θ, y outputs 1 ("neuronal firing").
[2.2] Simple Logic Circuit
[2.2.1] AND Gate
You can choose infinite numbers of combinations of (w1, w2, θ) to satisfy Fig. 2-2. For instance, (w1, w2, θ) = (0.5, 0.5, 0.7), (0.5, 0.5, 0.8), (1.0, 1.0, 1.0), etc. When x1 = x2 = 1, w1x1 + w2x2 > θ.
[2.2.2] NAND Gate and OR Gate
NAND = Not AND
You can choose infinite numbers of combinations of (w1, w2, θ) to satisfy Fig. 2-3. For instance, (w1, w2, θ) = (-0.5, -0.5, -0.7), (-0.5, -0.5, -0.8), (-1.0, -1.0, -1.0), etc. All you have to do is switch positive and negative signs for AND gate above. When x1 = x2 = 1, w1x1 + w2x2 > θ.
A perceptron can express AND, NAND, and OR logic circuits by using the same perceptron structure. The differences in the three gates are only parameters.
You (not computer) check the parameters above and/or come up with your own parameters. In machine learning, finding a parameter is automatically done by computer. Learning is deciding the best parameter; you have to choose or create a model (perceptron structure) and give data for learning.
[2.3] Implementation of Perceptron
[2.3.1] Simple Implementation: AND
>>> def AND(x1, x2):
... w1, w2, theta = 0.5, 0.5, 0.7
... tmp = w1*x1 + w2*x2
... if tmp <= theta:
... return 0
... elif tmp > theta:
... return 1
...
>>> AND(0,0)
0
>>> AND(1,0)
0
>>> AND(0,1)
0
>>> AND(1,1)
1
[2.3.2] Introduction of Weights and Bias
In (2.1), if θ = -b, then
y = 0 (w1x1 + w2x2 <= -b)
y = 1 (w1x1 + w2x2 > -b)
(2.2)
y = 0 (b + w1x1 + w2x2 <= 0)
y = 1 (b + w1x1 + w2x2 > 0)
When the sum of received numbers (b + w1x1 + w2x2) is larger than 0, y outputs 1 ("neuronal firing"). If not, y outputs 0.
>>> import numpy as np
>>> x = np.array([0,1]) # input
>>> w = np.array([0.5,0.5]) # weight
>>> b = -0.7 # bias
>>> w * x
array([ 0. , 0.5])
>>> np.sum(w * x)
0.5
>>> b + np.sum(w * x)
-0.19999999999999996
>>> b + np.sum(w * x) > 0
False
[2.3.3] Implementation with Weights and Bias: AND, NAND, and OR
>>> def AND(x1, x2):
... x = np.array([x1, x2])
... w = np.array([0.5, 0.5])
... b = -0.7
... tmp = b + np.sum(w*x)
... if tmp <= 0:
... return 0
... else:
... return 1
...
>>>
>>> AND(0,0)
0
>>> AND(1,0)
0
>>> AND(0,1)
0
>>> AND(1,1)
1
The weights w1 and w2 are parameters of the importance of the inputs. The bias b is a parameter to control whether or not the perceptron (AND) fires (outputs 1).
>>> def NAND(x1, x2):
... x = np.array([x1, x2])
... w = np.array([-0.5, -0.5]) # different weight parameters from the ones in AND
... b = 0.7 # different bias parameter from the one in AND (opposite sign)
... tmp = b + np.sum(w*x)
... if tmp <= 0:
... return 0
... else:
... return 1
...
>>>
>>> NAND(0,0)
1
>>> NAND(1,0)
1
>>> NAND(0,1)
1
>>> NAND(1,1)
0
>>> def OR(x1, x2):
... x = np.array([x1, x2])
... w = np.array([0.5, 0.5])
... b = -0.2 # different bias parameter from the one in AND
... tmp = b + np.sum(w*x)
... if tmp <= 0:
... return 0
... else:
... return 1
...
>>>
>>> OR(0,0)
0
>>> OR(1,0)
1
>>> OR(0,1)
1
>>> OR(1,1)
1
[2.4] Limitation of Perceptron
[2.4.1] XOR Gate
[2.4.2] Linearity and Non-linearity
A single perceptron cannot implement an XOR gate because of its linearity.
[2.5] Multi-layered Perceptrons
Multi-layered perceptrons can implement an XOR gate because of its non-linearity.
[2.5.1] A Combination of Existing Gates (AND, OR, and NAND)
Both s1 and s2 take x1 and x2 as inputs; y is outputs from AND that take inputs s1 and s2. y is outputs from XOR when x1 and x2 are inputs.
[2.5.2] Implementation of an XOR gate
>>> def XOR(x1, x2):
... s1 = NAND(x1, x2)
... s2 = OR(x1, x2)
... y = AND(s1, s2)
... return y
...
>>> XOR(0,0)
0
>>> XOR(1,0)
1
>>> XOR(0,1)
1
>>> XOR(1,1)
0
[2.6] NAND and Computers
Combination of NAND gates (perceptrons) can create a computer.
[2.7] Summary
[3] Neural Network
Weight parameters can be chosen by automatic learning by using neutral network; this is one of the most important characteristics of neural network.
[3.1] From Perceptron to Neural Network
[3.1.1] Examples of Neural Network
A neural network has (layer 0) input, (layer 1) middle or "hidden", and (layer 2) output layers. In this case, there are two (not three) layers that have weights.
[3.1.2] Revisit: Perceptron
y = h(x) (b + w1x1 +w2x2) (3.2)
[3.1.3] Activation Function
a = b + w1x1 +w2x2 (3.4)
[3.2] Activation Function
(3.3) is an activation function that does change output (0 or 1) based on its threshold; it is called a step (or staircase) function.
What if we choose non-step function? You can move on to the world of neutral network.
[3.2.1] Sigmoid Function
One of the most used activation functions in neutral network is a sigmoid function below.
h(x) = 1 / (1 + exp(-x)) (3.6)
The major difference between perceptrons and neural network is only an activation function. Other things like multi-layer structure of neuron and how to deliver a signal are basically the same.
If you re-start python, then run as follows on your Terminal on Mac OS (or cmd on Windows):
$ python
Python 3.6.0 |Anaconda 4.3.1 (x86_64)| (default, Dec 23 2016, 13:19:00)
[GCC 4.2.1 Compatible Apple LLVM 6.0 (clang-600.0.57)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>>
>>> import math
>>> math.exp(1)
2.718281828459045
>>> 1 / (1 + math.exp(-1))
0.7310585786300049
>>> 1 / (1 + math.exp(-2))
0.8807970779778823
[3.2.2] Implementing Step Functions
As you can see in (3.3), a step function returns 0 when input x <= 0) and returns 1 when input x > 0. The easiest implementation of a step function goes like this:
>>> def step_function(x):
... if x > 0:
... return 1
... else:
... return 0
...
>>> step_function(-1)
0
>>> step_function(0)
0
>>> step_function(1)
1
This is very easy to understand, but an argument x only accepts a real number (a floating-point number). It does not accept a NumPy array.
Not only for real numbers, but also for NumPy arrays, a function is defined and executed as follows:
>>> import numpy as np
>>> def step_function(x):
... y = x > 0
... return y.astype(np.int)
...
>>> x = np.array([-1.0, 1.0, 2.0])
>>> x
array([-1., 1., 2.])
>>> y = x > 0
>>> y
array([False, True, True], dtype=bool)
>>>
>>> y = y.astype(np.int)
>>> y
array([0, 1, 1])
>>>
>>> step_function(x)
array([0, 1, 1])
[3.2.3] Graph of Step Functions
If you re-start python, then run as follows on your Terminal on Mac OS (or cmd on Windows):
$ python
Python 3.6.0 |Anaconda 4.3.1 (x86_64)| (default, Dec 23 2016, 13:19:00)
[GCC 4.2.1 Compatible Apple LLVM 6.0 (clang-600.0.57)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>>
>>> import numpy as np
>>> import matplotlib.pylab as plt
>>>
>>> def step_function(x):
... return np.array(x > 0, dtype=np.int)
...
>>> x = np.arange(-5.0, 5.0, 0.1) # numbers from -5.0 to +4.9 (not +5.0), with 0.1 intervals
>>> y = step_function(x)
>>>
>>> plt.plot(x, y)
[<matplotlib.lines.Line2D object at 0x10c601e80>]
>>> plt.ylim(-0.1, 1.1) # specify y range
(-0.1, 1.1)
>>> plt.show()
[3.2.4] Implementing Sigmoid Functions
(3.6) can be written as follows:
>>> def sigmoid(x):
... return 1 / (1 + np.exp(-x)) # h(x) = 1 / (1 + exp(-x))
...
It should be noted that an argument x can accept a NumPy array.
>>> x = np.array([-1.0, 1.0, 2.0])
>>> x
array([-1., 1., 2.])
>>> sigmoid(x)
array([ 0.26894142, 0.73105858, 0.88079708])
>>> t = np.array([1.0, 2.0, 3.0])
>>> t
array([ 1., 2., 3.])
>>> 1.0 + t
array([ 2., 3., 4.])
>>> 1.0 / t
array([ 1. , 0.5 , 0.33333333])
>>> x = np.arange(-5.0, 5.0, 0.1)
>>> y = sigmoid(x)
>>> plt.plot(x, y)
[<matplotlib.lines.Line2D object at 0x119252978>]
>>> plt.ylim(-0.1, 1.1) # specify y range
(-0.1, 1.1)
>>> plt.show()
[3.2.5] Comparing Sigmoid Function and Step Function
>>> x = np.arange(-5.0, 5.0, 0.1)
>>> y1 = step_function(x)
>>> y2 = sigmoid(x)
>>> plt.plot(x, y1, 'r--') # 'r--' is an option for the dashed line
[<matplotlib.lines.Line2D object at 0x11056e390>]
>>> plt.plot(x, y2)
[<matplotlib.lines.Line2D object at 0x111e2dc88>]
>>> plt.ylim(-0.1, 1.1) # specify y range
(-0.1, 1.1)
>>> plt.show()
Like a dashed line above, neural network can handle with continuous real numbers as signals.
Both functions return smaller number (zero for the step function) when an input is smaller; they return larger number (one for the step function) when an input is larger. Also, no matter how small or large an input number is, an output from each function is between 0 and 1.
[3.2.6] Non-Linear Function
Both step function and sigmoid function are non-linear functions. In neural network, an activation function has to be non-linear. Why? Because it is non-sense if we use a linear function to have multi-layered neutral network; we can realize that by using one linear function. (e.g., a linear function h(x) = cx, y(x) = h(h(h(x)))) = c3 * x, then y(x) = ax, c3 = a. It can be expressed without a hidden layer.)
Therefore, to capitalize on multi-layering, an activation function has to be non-linear.
[3.2.7] ReLU Function
ReLU: Rectified Linear Unit
h(x) = x (x > 0), 0 (x <= 0) (3.7)
If an input is larger than zero, then input = output; if an input is equal to, or smaller than, zero, then output = 0.
>>> import numpy as np
>>> import matplotlib.pylab as plt
>>>
>>> def relu(x):
... return np.maximum(0, x)
...
>>> x = np.arange(-6.0, 6.0, 0.1)
>>> y = relu(x)
>>> plt.plot(x, y)
[<matplotlib.lines.Line2D object at 0x112b24d68>]
>>> plt.ylim(-1, 6)
(-1, 6)
>>> plt.show()
[3.3] Multi-Dimension Array Calculation
If you master calculations of NumPy multi-dimension arrays, it would be efficient to implement neural network.
[3.3.1] Multi-Dimension Array
A multi-dimension array could have numbers in one line (1-dimension), 2-dimension, 3-dimension, or N-dimension.
A one dimension array:
>>> import numpy as np
>>> A = np.array([1, 2, 3, 4])
>>> print(A)
[1 2 3 4]
>>> np.ndim(A)
1
>>> A.shape
(4,)
>>> A.shape[0]
4
# [1 2] is a first row while a series of 1 3 5 is column.
[3.3.2] Inner Product of Matrix
>>> A = np.array([[1, 2],[3, 4]])
>>> A.shape
(2, 2)
>>> B = np.array([[5, 6],[7, 8]])
>>> B.shape
(2, 2)
>>> np.dot(A, B)
array([[19, 22],
[43, 50]])
Calculation of a matrix AB goes like this:
row 1, column 1: 1*5 + 2*7 = 19
row 1, column 2: 1*6 + 2*8 = 22
row 1, column 1: 3*5 + 4*7 = 43
row 1, column 1: 3*6 + 4*8 = 50
>>> np.dot(B, A)
array([[23, 34],
[31, 46]])
As you can see above, the following matrix equation is not necessarily true: AB = BA
Computing an inverse matrix A-1 goes like this:
>>> np.linalg.inv(A)
array([[-2. , 1. ],
[ 1.5, -0.5]])
By definition, when a matrix A =
array([[a, b],
[c, d]])
then an inverse matrix A-1 is 1/(ad-bc) times
array([[d, -b],
[-c, a]])
In the case of A above,
a = 1, b = 2, c = 3, d = 4
1/(ad-bc) = 1/(1*4-2*3) = 1/(-2) = -0.5
A-1 =
array([[-0.5*4, -0.5*(-2)],
[-0.5*(-3), -0.5*1]])
=
array([[-2, 1],
[1.5, -0.5]])
>>> np.dot(A, np.linalg.inv(A))
array([[ 1.00000000e+00, 1.11022302e-16],
[ 0.00000000e+00, 1.00000000e+00]])
>>> np.dot(np.linalg.inv(A), A)
array([[ 1.00000000e+00, 4.44089210e-16],
[ 0.00000000e+00, 1.00000000e+00]])
To have integers, round can be used:
>>> np.round(np.dot(A, np.linalg.inv(A)), decimals=16)
array([[ 1.00000000e+00, 1.00000000e-16],
[ 0.00000000e+00, 1.00000000e+00]])
>>> np.round(np.dot(A, np.linalg.inv(A)), decimals=15)
array([[ 1., 0.],
[ 0., 1.]])
>>> np.round(np.dot(A, np.linalg.inv(A)), decimals=2)
array([[ 1., 0.],
[ 0., 1.]])
>>> np.dot(A, np.linalg.inv(A)).astype(np.int) # int does not work
array([[0, 0],
[0, 1]])
You can compute an inner product of i * j matrix A and j * k matrix B in this order. The number of columns for the first matrix (j) has to be equal to the number of rows for the second matrix (j). AB is an i*k matrix.
>>> A = np.array([[1, 2, 3],[4, 5, 6]])
>>> A.shape
(2, 3)
>>> B = np.array([[1, 2],[3, 4], [5, 6]])
>>> B.shape
(3, 2)
>>> np.dot(A, B)
array([[22, 28],
[49, 64]])
>>> C = np.array([[1, 2],[3, 4]])
>>> C.shape
(2, 2)
>>> A.shape
(2, 3)
>>> np.dot(A, C)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: shapes (2,3) and (2,2) not aligned: 3 (dim 1) != 2 (dim 0)
>>> np.dot(C, A)
array([[ 9, 12, 15],
[19, 26, 33]])
>>> A = np.array([[1, 2],[3, 4], [5, 6]])
>>> A.shape
(3, 2)
>>> B = np.array([7, 8])
>>> B.shape
(2,)
>>> np.dot(A, B)
array([23, 53, 83])
[3.3.2] Inner Product of Neural Network
>>> X = np.array([1, 2]) # x1 = 1, x2 = 2
>>> X.shape
(2,)
>>> print(X)
[1 2]
>>> W = np.array([[1, 3, 5],[2, 4, 6]])
>>> print(W)
[[1 3 5]
[2 4 6]]
>>> W.shape
(2, 3)
>>> Y = np.dot(X,W)
>>> print(Y) # y1 = 5, y2 = 11, y3 = 17
[ 5 11 17]
X =
[x1 x2]
W =
[[w1 w3 w5]
[w2 w4 w6]]
Y = XW =
[x1*w1+x2*w2 x1*w3+x2*w4 x1*w5+x2*w6] =
[y1 y2 y3]
X =
[1 2]
W =
[[1 3 5]
[2 4 6]]
Y = XW =
[1*1+2*2 1*3+2*4 1*5+2*6] =
[5 11 17]
[3.4] Implementing 3-layer Neural Network
A 3-layer neural network has (1) input layer, (2) first hidden layer, (3) second hidden layer, and (4) output layer. (1) consists of two neurons, (2) consists of three neurons, (3) consists of two neurons, and (4) consists of two neurons.
[3.4.1] Signs
Assume there are two neurons in (1) input layer, i.e., x1 and x2. Three neurons in (2) first hidden layer are
a1(1), a2(1), and a3(1). Weights can be written as follows:
wi j(n)
i: i-th neuron of the next layer
j: j-th neuron of the previous layer
n: n-th weighting
[3.4.2] Implementing Signal Transmission in Each Layer
a1(1) = b1(1) * 1 + (w1 1(1) * x1) + (w1 2(1) * x2) (3.8)
Bias b has only one index on the right hand side, bottom, because there is only one bias neuron.
If we use inner product of matrix, then (2) first hidden layer, a first layer, can be expressed as follows:
A(1) = B(1) + XW(1) (3.9)
A(1) = (a1(1), a2(1), a3(1))
B(1) = (b1(1), b2(1), b3(1))
X = (x1, x2)
W(1) = [ (w1 1(1), w2 1(1), w3 1(1)), (w1 2(1), w2 2(1), w3 2(1))]
>>> X = np.array([1.0, 0.5])
>>> W1 = np.array([[0.1, 0.3, 0.5],[0.2, 0.4, 0.6]])
>>> B1 = np.array([0.1, 0.2, 0.3])
>>>
>>> print(X.shape)
(2,)
>>> print(W1.shape)
(2, 3)
>>> print(B1.shape)
(3,)
>>>
>>> A1 = np.dot(X, W1) + B1
X has two numbers; it is given here.
B1 has three numbers because A(1) = (a1(1), a2(1), a3(1)), (2) hidden layer, has three values.
W1 has 2 * 3 numbers because X has two values X = (x1, x2) and A(1) = (a1(1), a2(1), a3(1)), (2) first hidden layer, has three components.
>>> def sigmoid(x):
... return 1 / (1 + np.exp(-x)) # h(x) = 1 / (1 + exp(-x))
...
>>> Z1 = sigmoid(A1)
>>> print(A1)
[ 0.3 0.7 1.1]
>>> print(Z1)
[ 0.57444252 0.66818777 0.75026011]
z1(1), output of (2) hidden layer, is defined as follows:
z1(1) = sigmoid(a1(1))
a1(1) = b1(1) + w1 1(1) x1 + w1 2(1) x2
-----
Let's move on to the implementation from (2) first hidden layer to (3) second hidden layer.
>>> W2 = np.array([[0.1, 0.4],[0.2, 0.5], [0.3, 0.6]])
>>> B2 = np.array([0.1, 0.2])
>>>
>>> print(Z1.shape)
(3,)
>>> print(W2.shape)
(3, 2)
>>> print(B2.shape)
(2,)
>>> A2 = np.dot(Z1, W2) + B2
>>> Z2 = sigmoid(A2)
Similarly, the implementation from (3) second hidden layer to (4) output layer is:
>>> def identity_function(x):
... return x
...
>>> W3 = np.array([[0.1, 0.3],[0.2, 0.4]])
>>> B3 = np.array([0.1, 0.2])
>>>
>>> A3 = np.dot(Z2, W3) + B3
>>> Y = identity_function(A3) # or Y = A3
An activation function in (4) output layer is expressed by σ() to differentiate it from other activation functions in hidden layers of (2) and (3). How to choose σ() depends on a nature of the problem to be solved. For a regression, it is generally identity function. For 2-class classification, it's sigmoid. For multi-class classification, it is a softmax function.
[3.4.3] Summary of Neural Network Implementation
>>> def init_network():
... network = {}
... network['W1'] = np.array([[0.1, 0.3, 0.5],[0.2, 0.4, 0.6]])
... network['b1'] = np.array([0.1, 0.2, 0.3])
... network['W2'] = np.array([[0.1, 0.4],[0.2, 0.5],[0.3, 0.6]])
... network['b2'] = np.array([0.1, 0.2])
... network['W3'] = np.array([[0.1, 0.3],[0.2, 0.4]])
... network['b3'] = np.array([0.1, 0.2])
... return network
...
>>> def forward(network, x):
... W1, W2, W3 = network['W1'], network['W2'], network['W3']
... b1, b2, b3 = network['b1'], network['b2'], network['b3']
... a1 = np.dot(x, W1) + b1
... z1 = sigmoid(a1)
... a2 = np.dot(z1, W2) + b2
... z2 = sigmoid(a2)
... a3 = np.dot(z2, W3) + b3
... y = identity_function(a3)
... return y
...
>>> network = init_network()
>>> x = np.array([1.0, 0.5])
>>> y = forward(network, x)
>>> print(y)
[ 0.31682708 0.69627909]
init_network() does the initialization of weights and biases. The output of it (a series of weights and biases that are necessary for each layer) is stored to a variable network.
forward() implements processes for input signal conversions to an output signal. forward means a direction from input to output. backward is opposite.
[3.5] Designing Output Layer
[3.5.1] Identity Function and Softmax Function
Neural network can be used for both classification and regression, but you need to choose an appropriate activation function accordingly. Generally speaking, a softmax function is for classifications (specifying a classification for a given input) and an identity function for regressions (estimating a certain number).
Identify function:
a1 -- σ() --> y1
a2 -- σ() --> y2
a3 -- σ() --> y3
Softmax function:
yk = exp(ak) / Σi=1n exp(ai) (3.10)
exp(x) = ex
exp(1) = e1 = 2.71828...
n: number of outputs
yk: k-th output
a1, a2, a3 -- σ() --> y1
a1, a2, a3 -- σ() --> y2
a1, a2, a3 -- σ() --> y3
>>> a = np.array([0.3, 2.9, 4.0])
>>> exp_a = np.exp(a)
>>> print(exp_a)
[ 1.34985881 18.17414537 54.59815003]
>>> sum_exp_a = np.sum(exp_a)
>>> print(sum_exp_a)
74.1221542102
>>> y = exp_a / sum_exp_a
>>> print(y)
[ 0.01821127 0.24519181 0.73659691]
Softmax function is defined as follows:
>>> def softmax(a):
... exp_a = np.exp(a)
... sum_exp_a = np.sum(exp_a)
... y = exp_a / sum_exp_a
... #
... return y
...
>>>
[3.5.2] A Problem When Implementing a Softmax Function
Exponential figures easily get large numbers.
>>> import numpy as np
>>> np.exp(10)
22026.465794806718
>>> np.exp(100)
2.6881171418161356e+43
>>> np.exp(1000)
__main__:1: RuntimeWarning: overflow encountered in exp
inf
Softmax function (3.10) can be modified to avoid an overflow problem above as follows:
yk = exp(ak) / Σi=1n exp(ai)
= C * exp(ak) / {C * Σi=1n exp(ai)}
= exp(ln(C)) * exp(ak) / {exp(ln(C)) * Σi=1n exp(ai)}
= exp(ak + ln(C)) / Σi=1n exp(ai + ln(C)) (3.11)
= exp(ak + C') / Σi=1n exp(ai + C')
ln(x) = loge(x) = y = ln(exp(y))
x = exp(y) = exp(ln(x))
Therefore, C = exp(ln(C))
What (3.11) means is that you can add (subtract) any number to (from) both numerator and denominator. In this case, it's C'. To avoid an overflow problem, C' is usually set to the maximum number within the inputs.
>>> a = np.array([1010, 1000, 990])
>>> a
array([1010, 1000, 990])
>>> np.exp(a) / np.sum(np.exp(a)) # softmax function calculation
array([ nan, nan, nan])
>>> # It is not calculated propoerly.
...
>>> c = np.max(a) #1010
>>> a - c
array([ 0, -10, -20])
>>> np.exp(a - c) / np.sum(np.exp(a - c)) # softmax function calculation
array([ 9.99954600e-01, 4.53978686e-05, 2.06106005e-09])
Finally, Softmax function implementation with an overflow prevention goes like this:
>>> def softmax(a):
... c = np.max(a)
... exp_a = np.exp(a - c) # overflow prevention
... sum_exp_a = np.sum(exp_a)
... y = exp_a / sum_exp_a
... return y
...
>>>
[3.5.3] Features of Softmax Function
If you use the softmax() defined above, a neural network output can be calculated as follows:
>>> a = np.array([0.3, 2.9, 4.0])
>>> y = softmax(a)
>>> print(y)
[ 0.01821127 0.24519181 0.73659691]
>>> np.sum(y)
1.0
As shown above, an output from a softmax function is a real number and varies from zero to one. Also, the sum of outputs is one; that is, an output from a softmax function is regarded as a probability.
Moreover, a softmax function in an output layer can be omitted because softmax (and exp) would not change magnitude relationships among outputs; the biggest number always gets the highest probability, because exp is a monotonically increasing function.
There are two phases in a deep learning: learning and inference (classification)
First, learning of a model is done. Second, in the inference phase, the model is used to infer by using unknown (out of sample) data. As described above, a softmax function in an output layer in the inference phase is usually omitted.
[3.5.4] A Number of Neurons in an Output Layer
A number of neurons in an output layer is usually set to the number of classifications; for example, if you want to classify an input image into numbers from zero to nine (10 classifications), then outputs in an output layer should be ten, i.e., y0, y1, ..., and y9. If y2 has the biggest number, then this neural network forecasts 2 as a plausible output.
[3.6] Recognition of Hand-Written Numbers
Please consider that the learning is done. By using parameters learned, we're going to implement an inference process (aka forward propagation) here.
[3.6.1] MNIST Data Set
>>> import sys, os
>>> os.getcwd() # show your current directory
>>> sys.path # show your system path
We are going to use mnist.py, which supports MNIST data set downloading and image data conversion to a NumPy array. There should be mnist.py in the dataset directory if you download files in the section [0] Prep. You have to be in a directory of ch01, ch02, or ch08 when you use the mnint.py.
>>> os.chdir(path) # a path to ch03, for instance, depends on your environment
>>> os.getcwd()
>>> import sys, os
>>> sys.path.append(os.pardir) # import files in a parent directory
>>> from dataset.mnist import load_mnist # load_mnist() function in dataset/mnist.py
>>> # It takes a few minutes for the first time.
... (x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
Downloading train-images-idx3-ubyte.gz ...
Done
Downloading train-labels-idx1-ubyte.gz ...
Done
Downloading t10k-images-idx3-ubyte.gz ...
Done
Downloading t10k-labels-idx1-ubyte.gz ...
Done
Converting train-images-idx3-ubyte.gz to NumPy Array ...
Done
Converting train-labels-idx1-ubyte.gz to NumPy Array ...
Done
Converting t10k-images-idx3-ubyte.gz to NumPy Array ...
Done
Converting t10k-labels-idx1-ubyte.gz to NumPy Array ...
Done
Creating pickle file ...
Done!
>>> # ouput each data shape
>>> print(x_train.shape) #(60000, 784)
(60000, 784)
>>> print(t_train.shape) #(60000, )
(60000,)
>>> print(x_test.shape) #(10000, 784)
(10000, 784)
>>> print(t_test.shape) #(10000, )
(10000,)
load_mnist() returns "(training image, training label), (test image, test label)" by using the loaded MNIST data.
If you look at:
load_mnist(normalize=True, flatten=True, one_hot_label=False)
normalize=True
means standardization (0.0 to 1.0) by using the input image
normalize=False
means no standardization, i.e., (0 to 255), an input image gets unchanged
flatten=True
stored as a one-dimension array with 784 components
flatten=False
stored as a three-dimension array with 1x28x28 components
one_hot_label=True
stored as an array with labels many 0s and only one 1 (correct answer)
one_hot_label=False
stored as an array only with correct labels e.g., 7, 2
You can find a script with the following code in ch03/mnist_show.py.
>>> import sys, os
>>> sys.path.append(os.pardir) # import files in a parent directory
>>> import numpy as np
>>> from dataset.mnist import load_mnist
>>> from PIL import Image
>>>
>>> def img_show(img):
... pil_img = Image.fromarray(np.uint8(img)) # data conversion from NumPy array to PIL (Python Image Library) data object
... pil_img.show()
...
>>> (x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False) # flatten=True makes an image one-dimension NumPy array
>>> img = x_train[0]
>>> label = t_train[0]
>>> print(label) #5
5
>>>
>>> print(img.shape)
(784,)
>>> img = img.reshape(28, 28) # reshape to the original image size
>>> print(img.shape)
(28, 28)
>>> img_show(img)
[3.6.2] Inference Process in Neural Network
Let's implement a neural network which does an inference processing for the MNIST data set. The neural network consists of 784 neurons (=28*28 pixels of an image file) in an input layer and 10 neurons (classifications from 0 to 10) in an output layer. Also, there are two hidden layers; the first has 50 and the second has 100 neurons in this case. The number 50 or 100 are arbitrary - you can choose whatever you want.
First off, change your current directory.
>>> import sys, os
>>> os.getcwd() # show your current directory
>>> sys.path # show your system path
You have to be in a directory of ch01, ch02, or ch08.
>>> os.chdir(path) # a path to ch03, for instance, depends on your environment
>>> os.getcwd()
>>> import sys, os
>>> sys.path.append(os.pardir) # import files in a parent directory
>>> import numpy as np
>>> from dataset.mnist import load_mnist
>>> from PIL import Image
You can find a script with the following code in ch03/nueralnet_mnist.py.
>>> def get_data():
... (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False) # normalize=True is normalization, a pre-processing process
... return x_test, t_test
...
>>> def init_network():
... with open("sample_weight.pkl", 'rb') as f:
... network = pickle.load(f)
... return network
...
>>> def predict(network, x):
... W1, W2, W3 = network['W1'], network['W2'], network['W3']
... b1, b2, b3 = network['b1'], network['b2'], network['b3']
... a1 = np.dot(x, W1) + b1
... z1 = sigmoid(a1)
... a2 = np.dot(z1, W2) + b2
... z2 = sigmoid(a2)
... a3 = np.dot(z2, W3) + b3
... y = softmax(a3)
... return y
>>> x, t = get_data()
>>> import pprint, pickle
>>> network = init_network()
>>> accuracy_cnt = 0
>>> for i in range(len(x)):
... y = predict(network, x[i])
... p = np.argmax(y) # an index with the highest probability
... if p == t[i]:
... accuracy_cnt += 1
>>> print("Accuracy:" + str(float(accuracy_cnt)/len(x)))
The result above will be:
Accuracy:0.9352
This means the classification with 93.52% accuracy.
Instead of writing each line of script, you can execute ch03/neuralnet_mnist.py on Terminal of MacOS (or cmd on Windows).
$ python neuralnet_mnist.py
Accuracy:0.9352
[3.6.3] Batch Processing
>>> x, _ = get_data()
>>> network = init_network()
>>> W1, W2, W3 = network['W1'], network['W2'], network['W3']
>>> x.shape
(10000, 784)
>>> x[0].shape
(784,)
>>> W1.shape
(784, 50)
>>> W2.shape
(50, 100)
>>> W3.shape
(100, 10)
Please make sure that dimensions of arrays are matched.
Fig. 3-26 Array Shapes
X W1 W2 W3 Y
784 784x50 50x100 100x10 10
When we have many images as inputs, such as, 100 images, then X would be 100x784 as an aggregated input.
Fig. 3-27 Array Shapes in a Batch Processing
X W1 W2 W3 Y
100x784 784x50 50x100 100x10 100x10
Let's implement a batch processing here.
>>> x, t = get_data()
>>> network = init_network()
>>>
>>> batch_size = 100 # size of batch
>>> accuracy_cnt = 0
>>>
>>> for i in range(0, len(x), batch_size):
... x_batch = x[i:i+batch_size]
... y_batch = predict(network, x_batch)
... p = np.argmax(y_batch, axis=1)
... accuracy_cnt += np.sum(p == t[i:i+batch_size])
...
>>>
>>> print("Accuracy:" + str(float(accuracy_cnt)/len(x)))
Accuracy:0.9352
range(start, end) is a list of integers from start to (end-1).
range(start, end, step) is a list of integers from start with an increase by step until (end-1).
>>> list(range(0, 10))
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> list(range(0, 10, 3))
[0, 3, 6, 9]
>>> list(range(0, 10, 5))
[0, 5]
>>> x = np.array([[0.1, 0.8, 0.1], [0.3, 0.1, 0.6], [0.2, 0.5, 0.3], [0.8, 0.1, 0.1]])
>>> y = np.argmax(x, axis=1) # argmax returns an index that contains the max number
>>> print(y)
[1 2 1 0]
>>> y = np.array([1, 2, 1, 0])
>>> t = np.array([1, 2, 0, 0])
>>> print(y == t)
[ True True False True]
>>> np.sum(y == t)
3
[3.7] Summary
[4] Learning in Neural Network
We introduce a loss function here. We try to find weight parameters that make the loss function value minimum. We use gradient (descent) method, which uses a slope of the function.
[4.1] Learning by Data
The feature of neural network is learning by data, namely, weight parameters can be automatically chosen by data. We are going to implement learning hand-written numbers of MNIST data set.
[4.1.1] Data Driven
A feature quality (amount of characteristic of an image) is a designed converter that properly extract output of intrinsic data from input data (images). A pattern of the feature quantity can be learned by machine learning techniques. An image data can be converted to vectors by using a feature quantity. However, the feature quantity has to be chosen or newly created by a human in a typical machine learning excluding deep learning.
Fig. 4-2
Image file --> (algorithm by a human) --> answer
Image file --> (feature quantity by a human) --> (machine learning like SVM, KNN) --> answer
Image file --> (neural network / deep learning or end-to-end machine learning) --> answer
No human intervention is indicated by bold characters.
[4.1.2] Training Data and Test Data
In machine learning, training data (sample data, teacher data) is used to specify a model with the best parameters first. Second, the trained model is tested by using test data (out-of-sample data). By this, we evaluate a general aptitude of the model. If you optimize the model only for sample data and the model does not work for out-of-sample data, then the model is in an overfitting problem. Avoiding overfitting is important in machine learning.
[4.2] Loss Function
A loss function in neural network learning is an index that evaluate how "bad" the neural network's ability is. Minimizing the loss function is maximizing the ability of the model.
[4.2.1] Mean Squared Error
One of the most famous loss functions is a mean squared error.
E = (1/2) * Σk exp(yk - tk)2 (4.1)
yk : neural network output
tk : training (teacher) data
k : dimension of data
>>> def mean_squared_error(y, t):
... return 0.5 * np.sum((y-t)**2)
...
>>>
>>> # one-hot expression
... # [2], the third component, is a right answer
...
>>> t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
>>>
>>> # Example 1: [2] has the highest probability (0.6)
... y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
>>>
>>> mean_squared_error(np.array(y), np.array(t))
0.097500000000000031
>>>
>>> # Example 2: [7] has the highest probability (0.6)
... y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
>>> mean_squared_error(np.array(y), np.array(t))
0.59750000000000003
As you can see above, the first loss function has smaller number (0.097500000000000031) and error. That is, the first example shows that outputs are well matched with training (teacher) data.
[4.2.2] Cross Entropy Error
E = -Σk tk * loge(yk) (4.2)
yk : neural network output
tk : training (teacher) data, correct answer label (one-hot expression with only one 1 and other 0s)
k : dimension of data
The first is better.
[4.2.3] Mini-batch Learning
If there are N training data, (4.2) can be written as follows.
E = -(1/N)Σn Σk tnk * loge(ynk) (4.3)
ynk : neural network output, n-th data, dimension k
tnk : training (teacher) data, correct answer label (one-hot expression with only one 1 and other 0s), n-th data, dimension k
n: n-th data
k : dimension of data
When learning in neutral network, each mini-batch (small chunk) of training data is chosen and learned.
Loading MNIST data set (dataset/mnist.py):
>>> import sys, os
>>> sys.path.append(os.pardir)
>>> import numpy as np
>>> from dataset.mnist import load_mnist
>>>
>>> (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
>>>
>>> print(x_train.shape) # 60,000 training data, 784(28x28)-dimension input data
(60000, 784)
>>> print(t_train.shape) # 10-dimension teacher data
(60000, 10)
Randomly choose 10 data from the training data.
>>> train_size = x_train.shape[0]
>>> train_size
60000
>>> batch_size = 10
>>> batch_mask = np.random.choice(train_size, batch_size)
>>> batch_mask
array([ 4957, 9951, 7070, 21607, 47857, 58590, 42236, 3033, 25998, 17251])
>>> x_batch = x_train[batch_mask]
>>> t_batch = t_train[batch_mask]
>>>
[4.2.4] Mini-batch Learning Implementation: Cross Entropy Error
>>> def cross_entropy_error(y, t):
... if y.ndim == 1:
... t = t.reshape(1, t.size)
... y = y.reshape(1, y.size)
... batch_size = y.shape[0]
... return -np.sum(t * np.log(y)) / batch_size
...
>>>
y: output of neural network
t: teacher data
If teacher data is given as a label, e.g., 2 or 7, not one-hot expression 0 or 1, then
>>> def cross_entropy_error(y, t):
... if y.ndim == 1:
... t = t.reshape(1, t.size)
... y = y.reshape(1, y.size)
... batch_size = y.shape[0]
... return -np.sum(np.log(y[np.arrange(batch_size), t])) / batch_size # different from the one above
...
>>>
[4.2.5] Why Loss Function?
If you look at a Sigmoid function, its differential is not zero anywhere. It is a very important feature to find the best parameters.
[4.3] Numerical Differentiation
[4.3.1] Differentiation
Definition of analytic differentiation:
df(x) / dx = lim h --> 0 {f(x+h) - f(x)} / h (4.4)
>>> def numerical_diff(f, x):
... h = 1e-4 #0.0001
... return (f(x+h) - f(x-h)) / (2*h)
...
>>>
[4.3.2] An Example of Numerical Differentiation
f(x) = y = 0.01x^2 + 0.1x (4.5)
>>> def function_1(x):
... return 0.01*x**2 + 0.1*x
...
>>>
Next, draw the function y = f(x) above.
>>> import numpy as np
>>> import matplotlib.pylab as plt
>>>
>>> x = np.arange(0.0, 20.0, 0.1) # x array, from 0 to 20, increase by 0.1
>>> y = function_1(x)
>>> plt.xlabel("x")
<matplotlib.text.Text object at 0x12939a630>
>>> plt.ylabel("f(x)")
<matplotlib.text.Text object at 0x1293b4cf8>
>>> plt.plot(x, y)
[<matplotlib.lines.Line2D object at 0x12956e1d0>]
>>> plt.show()
>>> numerical_diff(function_1, 5)
0.1999999999990898
>>> numerical_diff(function_1, 10)
0.2999999999986347
df(x) / dx = 0.02x + 0.1
>>> 0.02 * 5 + 0.1
0.2
>>> 0.02 * 10 + 0.1
0.30000000000000004
Errors are very small as you can see above and in the source code of ch04/gradient_1d.py.
[4.3.3] Partial Differentiation
f(x0, x1) = x0^2 + x1^2 (4.6)
Note that there are two types of variables. Or, by using X, Y, and Z, it can be written as follows.
Z = f(X, Y) = X^2 + Y^2 (4.6)'
>>> import numpy as np
>>> import matplotlib.pylab as plt
>>> from mpl_toolkits.mplot3d import Axes3D
>>> x = np.arange(-3.0, 3.0, 0.1)
>>> y = np.arange(-3.0, 3.0, 0.1)
>>> X, Y = np.meshgrid(x,y)
>>> print("x=", x)
>>> print("X=", X)
>>> print("y=", y)
>>> print("Y=", Y)
>>> def function_2(X, Y):
... return X**2 + Y**2
...
>>>
>>> Z = function_2(X, Y)
>>> print("Z=", Z)
>>> fig = plt.figure()
>>> ax = Axes3D(fig)
>>> ax.plot_wireframe(X, Y, Z)
<mpl_toolkits.mplot3d.art3d.Line3DCollection object at 0x116bc22b0>
>>> ax.set_xlabel("X")
<matplotlib.text.Text object at 0x10d13b240>
>>> ax.set_ylabel("Y")
<matplotlib.text.Text object at 0x10d14cd30>
>>> ax.set_zlabel("Z")
<matplotlib.text.Text object at 0x10d15c748>
>>> plt.show()
Fig 4-8 Z = f(X, Y) = X^2 + Y^2
z = f(x, y) = x^2 + y^2
∂ f(x, y) / ∂x = 2 * x
∂ f(x, y) / ∂y = 2 * y
When x = 3, y = 4,
∂ f(x, y) / ∂x = 2 * x = 2 * 3 = 6
When x = 3, y = 4,
∂ f(x, y) / ∂y = 2 * y = 2 * 4 = 8
>>> def numerical_diff(f, x):
... h = 1e-4 #0.0001
... return (f(x+h) - f(x-h)) / (2*h)
...
>>>
>>> def function_tmp1(x):
... return x*x + 4.0**2.0
...
>>> numerical_diff(function_tmp1, 3.0)
6.00000000000378
>>> def function_tmp2(y):
... return 3.0**2.0 + y*y
...
>>> numerical_diff(function_tmp2, 4)
7.999999999999119
>>>
[4.4] Gradient
>>> import numpy as np
>>> def function_2(x):
... return x[0]**2 + x[1]**2
...
>>>
>>> def numerical_gradient(f,x):
... h = 1e-4 # 0.0001
... grad = np.zeros_like(x)
... #
... for idx in range(x.size):
... tmp_val = x[idx]
... # f(x+h) calculation
... x[idx] = tmp_val + h
... fxh1 = f(x)
... #
... # f(x-h) calculation
... x[idx] = tmp_val - h
... fxh2 = f(x)
... #
... grad[idx] = (fxh1 - fxh2) / (2*h)
... x[idx] = tmp_val
... #
... return grad
...
>>>
>>> numerical_gradient(function_2, np.array([3.0, 4.0]))
array([ 6., 8.])
>>> numerical_gradient(function_2, np.array([0.0, 2.0]))
array([ 0., 4.])
>>> numerical_gradient(function_2, np.array([3.0, 0.0]))
array([ 6., 0.])
It should be noted directions that each gradient points lowers a value of a loss function the most. That does not necessarily means that you can find a minimum value; rather it could be a local minimal value or saddle point.
You can draw Fig 4-9 by ch04/gradient_2d.py:
$ python gradient_2d.py
[4.4.1] Gradient Method
In a gradient method, you continuously check a direction of a gradient and travel a constant distance in order to gradually lower a value of a loss function. (This is a gradient descent method and the opposite is a gradient ascent method.) It is a popular way in an optimization of machine learning.
Gradient method:
x0 = x0 - η ∂f / ∂x0
x1 = x1 - η ∂f / ∂x1
(4.7)
η: learning rate (quantity of an update; how much should it learn and update a parameter)
Gradient descent method:
>>> def gradient_descent(f, init_x, lr=0.01, step_num=100):
... x = init_x
... #
... for i in range(step_num):
... grad = numerical_gradient(f, x)
... x -= lr * grad
... #
... return x
...
>>>
f : a function to be optimized
init_x : initial value
lr : learning rate
step_num : number of steps
Question: What is the minimum value of f(x0, x1) = x0^2 + x1^2 ? Use a gradient method.
>>> def function_2(x):
... return x[0]**2 + x[1]**2
...
>>>
>>> init_x = np.array([-3.0, 4.0])
>>> gradient_descent(function_2, init_x=init_x, lr=1e-10, step_num=100)
array([-2.99999994, 3.99999992])
>>> init_x = np.array([-3.0, 4.0])
>>> gradient_descent(function_2, init_x=init_x, lr=0.01, step_num=100)
array([-0.39785867, 0.53047822])
>>> init_x = np.array([-3.0, 4.0])
>>> gradient_descent(function_2, init_x=init_x, lr=0.1, step_num=100)
array([ -6.11110793e-10, 8.14814391e-10])
>>> init_x = np.array([-3.0, 4.0])
>>> gradient_descent(function_2, init_x=init_x, lr=1, step_num=100)
array([-3., 4.])
>>> init_x = np.array([-3.0, 4.0])
>>> gradient_descent(function_2, init_x=init_x, lr=10, step_num=100)
array([ -2.58983747e+13, -1.29524862e+12])
A learning rate (lr) should not be too big or small. If it's too big, the results get bigger; if it's too small, the results get updated only a little bit. The most important thing for a human is to choose an appropriate learning rate (so-called hyper parameter). Hyper parameters have to be found by trial and error.
You can draw Fig 4-10 by ch04/gradient_method.py:
$ python gradient_method.py
[4.4.2] Gradient against neural network
References
[A] Learn Python Pro by Sololearn Inc
iPhone App for very basic Python programming
https://appsto.re/jp/mHh34.i
[B] Introducing Python: Modern Computing in Simple Packages 1st Edition
For basic Python programming
Amazon.com
Amazon.co.jp
[C] Python for Data Analysis: Data Wrangling with Pandas, NumPy, and IPython 2nd Edition
For NumPy
Amazon.com
Amazon.co.jp
[D] Scipy Lecture Notes
For NumPy and Matplotlib
http://www.scipy-lectures.org
For programs used in this article, visit the following website > Clone or download > Download ZIP
https://github.com/oreilly-japan/deep-learning-from-scratch
Anaconda distribution for data analysis, which includes NumPy (numerical calculation) and Matplotlib (graph drawing)
https://www.continuum.io/downloads
Choose Python 3.X for your platform (in my case, Mac OS)
Install the downloaded pkg file.
After the installation, open Terminal on Mac OS (or cmd on Windows) and enter the following code:
$ python --version
Python 3.6.0 :: Anaconda 4.3.1 (x86_64)
This shows you that the installation has been successfully ended.
Start the Python interpreter:
$ python
Python 3.6.0 |Anaconda 4.3.1 (x86_64)| (default, Dec 23 2016, 13:19:00)
[GCC 4.2.1 Compatible Apple LLVM 6.0 (clang-600.0.57)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>>
[1] Intro
[1.3.1] Numerical Calculation
>>> 1 + 2
3
>>> 1 - 2
-1
>>> 4 * 5
20
>>> 7 / 5
1.4
>>> 3 ** 2
9
[1.3.2] Data Type
>>> type(10)
<class 'int'>
>>> type(2.718)
<class 'float'>
>>> type("Hello")
<class 'str'>
[1.3.3] Variable
>>> x = 10 #initialization
>>> print(x)
10
>>> x = 100 # substitute
>>> print(x)
100
>>> y = 3.14
>>> x * y
314.0
>>> type(x * y)
<class 'float'>
[1.3.4] List
>>> a = [1, 2, 3, 4, 5] # create a list
>>> print(a)
[1, 2, 3, 4, 5]
>>> type(a)
<class 'list'>
>>> len(a)
5
>>> a[0] # access the first element
1
>>> a[4] # access the last (fifth) element
5
>>> a[4] = 99 # substitute the last (fifth) element with 99
>>> print(a)
[1, 2, 3, 4, 99]
>>> a[0:2] # Show 1st (0) and 2nd (1) elements, but not 3rd (2) elements.
[1, 2]
>>> a[1:] # Show elements from the second (1) to the last.
[2, 3, 4, 99]
>>> a[:3] # Show elements from the first (0) to the third (2); the fourth(3) is NOT included.
[1, 2, 3]
>>> a[:-1] # Show elements from the first (0) to the last minus 1 (fourth, 3).
[1, 2, 3, 4]
>>> a[:-2] # Show elements from the first (0) to the last minus 2 (third, 2).
[1, 2, 3]
[1.3.5] Dictionary
>>> me = {'height':180} # Create a dictionary.
>>> me['height'] # Access an element of the dictionary.
180
>>> me['weight'] = 70 # Add a new element to the dictionary.
>>> print(me)
{'height': 180, 'weight': 70}
[1.3.6] Boolean
>>> hungry = True
>>> sleepy = False
>>> type(hungry)
<class 'bool'>
>>> not hungry # not True, i.e., False
False
>>> hungry and sleepy # True and False, i.e., False
False
>>> hungry or sleepy # True or False, i.e., True
True
[1.3.7] if
>>> hungry = True
>>> if hungry:
... print("I'm hungry.") # You have to put at least single space (ideally four spaces) after if
...
I'm hungry.
>>> hungry = False
>>> if hungry:
... print("I'm hungry") # You have to put at least single space (ideally four spaces) after if
... else:
... print("I'm not hungry.")
... print("I'm sleepy.")
...
I'm not hungry.
I'm sleepy.
[1.3.8] for
>>> for i in [1, 2, 3]:
... print(i) # four spaces on the left hand side
...
1
2
3
[1.3.9] Function
>>> def hello():
... print("Hello, World!") # four spaces on the left hand side
...
>>> hello()
Hello, World!
>>> def hello(object):
... print("Hello, " + object + "!") # four spaces on the left hand side
...
>>> hello("everyone")
Hello, everyone!
To finish the Python interpreter, Ctrl-D for Mac OS and Linux, Ctrl-Z and Enter for Windows.
[1.4] Python script file
[1.4.1] Saving a new Python script file
Create a new file hungry.py that only includes the following line:
print("I'm hungry!")
Open Terminal on Mac OS (or cmd on Windows) and then move to the directory where you saved the file hungry.py.
$ pwd # check your present working directory
$ cd # Change directory to the directory where you saved the file hungry.py. You need to put absolute or relative path after "cd" command.
$ python hungry.py
I'm hungry!
[1.4.2] Class
In [1.3.2] Data Type, you see data types like int or str, which are checked by a built-in function, type(). You can define a new class and data type.
Create a man.py which includes the following codes:
class Man: # a new class name
def __init__(self, name): # __init___ is a special method. It is also a constructor, for initialization, which is called once when an instance of the class is created
self.name = name # self is an instance of itself. self.(attribution name) is to create an instance and access it.
print("Initialized!")
def hello(self):
print("Hello " + self.name + "!")
def goodbye(self):
print("Good-bye " + self.name + "!")
m = Man("David") # m is an instance (object)
m.hello()
m.goodbye()
On your Terminal on Mac OS (or cmd on Windows), run as follows:
$ python man.py
Initialized!
Hello David!
Good-bye David!
[1.5] NumPy
In implementations of Deep Learning, there are many calculations of arrays and matrices. Numpy array class (numpy.array) has convenient methods that can be used for deep learning implementations.
[1.5.1] Importing NumPy
On your Terminal on Mac OS (or cmd on Windows), run as follows:
$ python
Python 3.6.0 |Anaconda 4.3.1 (x86_64)| (default, Dec 23 2016, 13:19:00)
[GCC 4.2.1 Compatible Apple LLVM 6.0 (clang-600.0.57)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>>
>>> import numpy as np # import numpy libraries; from now on, you can refer to numpy methods np.*
[1.5.2] NumPy array
np.array() receives a Python list and creates a NumPy array (numpy.ndarray).
>>> x = np.array([1.0, 2.0, 3.0])
>>> print(x)
[ 1. 2. 3.]
>>> type(x)
<class 'numpy.ndarray'>
[1.5.3] NumPy mathematical calculation
Example of element-wise calculation:
>>> x = np.array([1.0, 2.0, 3.0])
>>> y = np.array([2.0, 4.0, 6.0])
>>> x + y # addition in each element
array([ 3., 6., 9.])
>>> x - y # subtraction in each element
array([-1., -2., -3.])
>>> x * y # element-wise product
array([ 2., 8., 18.])
>>> x / y # element-wise division
array([ 0.5, 0.5, 0.5])
It should be noted that number of elements in x and y are the same. If not, it causes an error.
NumPy array and single scalar calculation (broadcast):
>>> x = np.array([1.0, 2.0, 3.0])
>>> x / 2.0
array([ 0.5, 1. , 1.5])
[1.5.4] NumPy N-dimension array
>>> A = np.array([[1, 2], [3,4]])
>>> print(A)
[[1 2]
[3 4]]
>>> A.shape #
(2, 2)
>>> A.dtype
dtype('int64')
>>> AA = np.array([[1, 2], [3,4], [5,6]])
>>> AA.shape # (# of row, # of column)
(3, 2)
>>> print(AA)
[[1 2]
[3 4]
[5 6]]
>>> print(A)
[[1 2]
[3 4]]
>>> B = np.array([[3, 0], [0, 6]])
>>> A + B
array([[ 4, 2],
[ 3, 10]])
>>> A * B # not a matrix calculation, just a element-wise calculation
array([[ 3, 0],
[ 0, 24]])
>>> print(A)
[[1 2]
[3 4]]
>>> A * 10
array([[10, 20],
[30, 40]])
[1.5.5] Broadcast
>>> A = np.array([[1, 2], [3,4]])
>>> B = np.array([10, 20])
>>> A * B # element-wise calculation by broadcast
array([[10, 40],
[30, 80]])
[1.5.6] Element-wise Access
>>> X = np.array([[51, 55], [14, 19], [0, 4]])
>>> print(X)
[[51 55]
[14 19]
[ 0 4]]
>>> X[0]
array([51, 55])
>>> X[0][0]
51
>>> X[0][1]
55
>>> for i in X:
... print(i)
...
[51 55]
[14 19]
[0 4]
>>> X = X.flatten() # X is converted to 1-dimension array
>>> print(X)
[51 55 14 19 0 4]
>>> X[np.array([0, 2, 4])]
array([51, 14, 0])
>>> X > 15
array([ True, True, False, True, False, False], dtype=bool)
>>> X[X > 15] # extract elements with True
array([51, 55, 19])
Python is dynamic (script) language and it is relatively slow in processing. NumPy implements major processes with C/C++, faster static (compiler) languages.
[1.6] Matplotlib
Matplotlib is a library for drawing graphs.
[1.6.1] Drawing a simple graph
>>> import numpy as np
>>> import matplotlib.pyplot as plt # module pyplot for drawing graphs
>>> x = np.arange(0, 6, 0.1) # from 0 to 6, with increments by 0.1
>>> x
array([ 0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ,
1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2. , 2.1,
2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3. , 3.1, 3.2,
3.3, 3.4, 3.5, 3.6, 3.7, 3.8, 3.9, 4. , 4.1, 4.2, 4.3,
4.4, 4.5, 4.6, 4.7, 4.8, 4.9, 5. , 5.1, 5.2, 5.3, 5.4,
5.5, 5.6, 5.7, 5.8, 5.9])
>>> y = np.sin(x)
>>> plt.plot(x, y)
[<matplotlib.lines.Line2D object at 0x11d552160>]
>>> plt.show()
Ctrl-Z brings you back to Terminal on Mac OS. If you do, then run the following command to get back to Python:
$ python
[1.6.2] pyplot
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> x = np.arange(0, 6, 0.1)
>>> y1 = np.sin(x)
>>> y2 = np.cos(x)
>>>
>>> plt.plot(x, y1, label="sin")
[<matplotlib.lines.Line2D object at 0x11671a550>]
>>> plt.plot(x, y2, linestyle = "--", label="cos")
[<matplotlib.lines.Line2D object at 0x10cd3afd0>]
>>> plt.xlabel("x")
<matplotlib.text.Text object at 0x113b239e8>
>>> plt.ylabel("y")
<matplotlib.text.Text object at 0x1166d60b8>
>>> plt.title('sin & cos')
<matplotlib.text.Text object at 0x1166dd748>
>>> plt.legend()
<matplotlib.legend.Legend object at 0x11671a748>
>>> plt.show()
Ctrl-Z brings you back to Terminal on Mac OS. If you do, then run the following command to get back to Python:
$ python
[1.6.3] Show pictures
>>> import matplotlib.pyplot as plt
>>> from matplotlib.image import imread
>>>
>>> img = imread('figure_1.png') # specify a file name (or path) to your image file
>>> plt.imshow(img)
<matplotlib.image.AxesImage object at 0x11cd8a470>
>>> plt.show()
[1.7] Summary
- Python is a simple and open-source language which is easy to learn.
- Python 3.X is used here for deep learning.
- NumPy and Matplotlib are used as external libraries.
- To run Python, we have "interpreter" and "script-file" modes.
- In Python, function are class modules are used to summarize implementations.
- NumPy has many convenient methods to manipulate multiple-dimension arrays.
[2] Perceptron
A perceptron is an algorithm which is an origin of neural network (deep learning).
[2.1] Perceptron
A perceptron (technically artificial neuron or simple perceptron) receives several signals as inputs and returns one output. Signals of a perception are either 0 (a signal is NOT delivered to the next) or 1 (a signal is delivered to the next).
For instance,
x1: input signal 1
x2: input signal 2
w1: weight of the signal 1
w2: weight of the signal 2
y: this receives w1x1 and w2x2
x1, x2, and y are called neurons or nodes.
(2.1)
y = 0 (w1x1 + w2x2 <= θ)
y = 1 (w1x1 + w2x2 > θ)
θ is a threshold. When the sum of received numbers (w1x1 + w2x2) is larger than the threshold θ, y outputs 1 ("neuronal firing").
[2.2] Simple Logic Circuit
[2.2.1] AND Gate
x1
|
x2
| y |
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
You can choose infinite numbers of combinations of (w1, w2, θ) to satisfy Fig. 2-2. For instance, (w1, w2, θ) = (0.5, 0.5, 0.7), (0.5, 0.5, 0.8), (1.0, 1.0, 1.0), etc. When x1 = x2 = 1, w1x1 + w2x2 > θ.
[2.2.2] NAND Gate and OR Gate
x1
|
x2
| y |
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
You can choose infinite numbers of combinations of (w1, w2, θ) to satisfy Fig. 2-3. For instance, (w1, w2, θ) = (-0.5, -0.5, -0.7), (-0.5, -0.5, -0.8), (-1.0, -1.0, -1.0), etc. All you have to do is switch positive and negative signs for AND gate above. When x1 = x2 = 1, w1x1 + w2x2 > θ.
x1
|
x2
| y |
0
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
You can choose infinite numbers of combinations of (w1, w2, θ) to satisfy Fig. 2-4. For instance, (w1, w2, θ) = (0.5, 0.5, 0.4), (0.5, 0.5, 0.3), (1.0, 1.0, 0.9), etc. When x1 = 1 and/or x2 = 1, w1x1 + w2x2 > θ.
A perceptron can express AND, NAND, and OR logic circuits by using the same perceptron structure. The differences in the three gates are only parameters.
You (not computer) check the parameters above and/or come up with your own parameters. In machine learning, finding a parameter is automatically done by computer. Learning is deciding the best parameter; you have to choose or create a model (perceptron structure) and give data for learning.
[2.3] Implementation of Perceptron
[2.3.1] Simple Implementation: AND
>>> def AND(x1, x2):
... w1, w2, theta = 0.5, 0.5, 0.7
... tmp = w1*x1 + w2*x2
... if tmp <= theta:
... return 0
... elif tmp > theta:
... return 1
...
>>> AND(0,0)
0
>>> AND(1,0)
0
>>> AND(0,1)
0
>>> AND(1,1)
1
[2.3.2] Introduction of Weights and Bias
In (2.1), if θ = -b, then
y = 0 (w1x1 + w2x2 <= -b)
y = 1 (w1x1 + w2x2 > -b)
(2.2)
y = 0 (b + w1x1 + w2x2 <= 0)
y = 1 (b + w1x1 + w2x2 > 0)
b: bias
w1, w2: weight
When the sum of received numbers (b + w1x1 + w2x2) is larger than 0, y outputs 1 ("neuronal firing"). If not, y outputs 0.
>>> import numpy as np
>>> x = np.array([0,1]) # input
>>> w = np.array([0.5,0.5]) # weight
>>> b = -0.7 # bias
>>> w * x
array([ 0. , 0.5])
>>> np.sum(w * x)
0.5
>>> b + np.sum(w * x)
-0.19999999999999996
>>> b + np.sum(w * x) > 0
False
[2.3.3] Implementation with Weights and Bias: AND, NAND, and OR
>>> def AND(x1, x2):
... x = np.array([x1, x2])
... w = np.array([0.5, 0.5])
... b = -0.7
... tmp = b + np.sum(w*x)
... if tmp <= 0:
... return 0
... else:
... return 1
...
>>>
>>> AND(0,0)
0
>>> AND(1,0)
0
>>> AND(0,1)
0
>>> AND(1,1)
1
The weights w1 and w2 are parameters of the importance of the inputs. The bias b is a parameter to control whether or not the perceptron (AND) fires (outputs 1).
>>> def NAND(x1, x2):
... x = np.array([x1, x2])
... w = np.array([-0.5, -0.5]) # different weight parameters from the ones in AND
... b = 0.7 # different bias parameter from the one in AND (opposite sign)
... tmp = b + np.sum(w*x)
... if tmp <= 0:
... return 0
... else:
... return 1
...
>>>
>>> NAND(0,0)
1
>>> NAND(1,0)
1
>>> NAND(0,1)
1
>>> NAND(1,1)
0
... x = np.array([x1, x2])
... w = np.array([0.5, 0.5])
... b = -0.2 # different bias parameter from the one in AND
... tmp = b + np.sum(w*x)
... if tmp <= 0:
... return 0
... else:
... return 1
...
>>>
>>> OR(0,0)
0
>>> OR(1,0)
1
>>> OR(0,1)
1
>>> OR(1,1)
1
[2.4] Limitation of Perceptron
[2.4.1] XOR Gate
x1
|
x2
| y |
0
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
[2.4.2] Linearity and Non-linearity
A single perceptron cannot implement an XOR gate because of its linearity.
[2.5] Multi-layered Perceptrons
Multi-layered perceptrons can implement an XOR gate because of its non-linearity.
[2.5.1] A Combination of Existing Gates (AND, OR, and NAND)
x1
|
x2
| s1 (NAND) | s2 (OR) | y (AND) |
0
|
0
|
1
| 0 | 0 |
1
|
0
|
1
| 1 | 1 |
0
|
1
|
1
| 1 | 1 |
1
|
1
|
0
| 1 | 0 |
[2.5.2] Implementation of an XOR gate
>>> def XOR(x1, x2):
... s1 = NAND(x1, x2)
... s2 = OR(x1, x2)
... y = AND(s1, s2)
... return y
...
>>> XOR(0,0)
0
>>> XOR(1,0)
1
>>> XOR(0,1)
1
>>> XOR(1,1)
0
The more (deeper) multi-layered perceptrons, the more complicated / flexible expressions the combination of the perceptions can make.
[2.6] NAND and Computers
Combination of NAND gates (perceptrons) can create a computer.
[2.7] Summary
- A perceptron is an algorithm with an input (inputs) and an output. Given certain inputs, an output based on the inputs will be generated.
- Perceptrons set weights and bias as parameters.
- A perceptron can express a logical circuit like AND and OR gates; an XOR gate cannot be expressed by a single(-layer) perceptron.
- An XOR gate can be build by multi-layered perceptrons.
- A sigle-layer perceptron can only express a linearity while multi-layered perceptrons can express non-linearity.
- Multi-layered perceptrons can express computer theoretically.
[3] Neural Network
Weight parameters can be chosen by automatic learning by using neutral network; this is one of the most important characteristics of neural network.
[3.1] From Perceptron to Neural Network
[3.1.1] Examples of Neural Network
A neural network has (layer 0) input, (layer 1) middle or "hidden", and (layer 2) output layers. In this case, there are two (not three) layers that have weights.
[3.1.2] Revisit: Perceptron
h(x) = 0 (x <= 0), 1 (x > 0) (3.3)
[3.1.3] Activation Function
a = b + w1x1 +w2x2 (3.4)
y = h(a) (3.4)
h(a) = 0 (a <= 0), 1 (a > 0) (3.3')
h(a) : activation function
[3.2] Activation Function
(3.3) is an activation function that does change output (0 or 1) based on its threshold; it is called a step (or staircase) function.
What if we choose non-step function? You can move on to the world of neutral network.
[3.2.1] Sigmoid Function
One of the most used activation functions in neutral network is a sigmoid function below.
h(x) = 1 / (1 + exp(-x)) (3.6)
The major difference between perceptrons and neural network is only an activation function. Other things like multi-layer structure of neuron and how to deliver a signal are basically the same.
If you re-start python, then run as follows on your Terminal on Mac OS (or cmd on Windows):
$ python
Python 3.6.0 |Anaconda 4.3.1 (x86_64)| (default, Dec 23 2016, 13:19:00)
[GCC 4.2.1 Compatible Apple LLVM 6.0 (clang-600.0.57)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>>
>>> import math
>>> math.exp(1)
2.718281828459045
>>> 1 / (1 + math.exp(-1))
0.7310585786300049
>>> 1 / (1 + math.exp(-2))
0.8807970779778823
[3.2.2] Implementing Step Functions
As you can see in (3.3), a step function returns 0 when input x <= 0) and returns 1 when input x > 0. The easiest implementation of a step function goes like this:
>>> def step_function(x):
... if x > 0:
... return 1
... else:
... return 0
...
>>> step_function(-1)
0
>>> step_function(0)
0
>>> step_function(1)
1
Not only for real numbers, but also for NumPy arrays, a function is defined and executed as follows:
>>> import numpy as np
>>> def step_function(x):
... y = x > 0
... return y.astype(np.int)
...
>>> x = np.array([-1.0, 1.0, 2.0])
>>> x
array([-1., 1., 2.])
>>> y = x > 0
>>> y
array([False, True, True], dtype=bool)
>>>
>>> y = y.astype(np.int)
>>> y
array([0, 1, 1])
>>>
>>> step_function(x)
array([0, 1, 1])
[3.2.3] Graph of Step Functions
If you re-start python, then run as follows on your Terminal on Mac OS (or cmd on Windows):
$ python
Python 3.6.0 |Anaconda 4.3.1 (x86_64)| (default, Dec 23 2016, 13:19:00)
[GCC 4.2.1 Compatible Apple LLVM 6.0 (clang-600.0.57)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>>
>>> import numpy as np
>>> import matplotlib.pylab as plt
>>>
>>> def step_function(x):
... return np.array(x > 0, dtype=np.int)
...
>>> x = np.arange(-5.0, 5.0, 0.1) # numbers from -5.0 to +4.9 (not +5.0), with 0.1 intervals
>>> y = step_function(x)
>>>
>>> plt.plot(x, y)
[<matplotlib.lines.Line2D object at 0x10c601e80>]
>>> plt.ylim(-0.1, 1.1) # specify y range
(-0.1, 1.1)
>>> plt.show()
Fig. 3-6 Step Function
As you can see in Fig. 3-6, the step function's output changes from zero to one (or from one to zero) at x = 0. This looks like a staircase, so it is also called a staircase function.[3.2.4] Implementing Sigmoid Functions
(3.6) can be written as follows:
>>> def sigmoid(x):
... return 1 / (1 + np.exp(-x)) # h(x) = 1 / (1 + exp(-x))
...
It should be noted that an argument x can accept a NumPy array.
>>> x = np.array([-1.0, 1.0, 2.0])
>>> x
array([-1., 1., 2.])
>>> sigmoid(x)
array([ 0.26894142, 0.73105858, 0.88079708])
>>> t = np.array([1.0, 2.0, 3.0])
>>> t
array([ 1., 2., 3.])
>>> 1.0 + t
array([ 2., 3., 4.])
>>> 1.0 / t
array([ 1. , 0.5 , 0.33333333])
>>> x = np.arange(-5.0, 5.0, 0.1)
>>> y = sigmoid(x)
>>> plt.plot(x, y)
[<matplotlib.lines.Line2D object at 0x119252978>]
>>> plt.ylim(-0.1, 1.1) # specify y range
(-0.1, 1.1)
>>> plt.show()
Fig. 3-7 Sigmoid Function
[3.2.5] Comparing Sigmoid Function and Step Function
>>> x = np.arange(-5.0, 5.0, 0.1)
>>> y1 = step_function(x)
>>> y2 = sigmoid(x)
>>> plt.plot(x, y1, 'r--') # 'r--' is an option for the dashed line
[<matplotlib.lines.Line2D object at 0x11056e390>]
>>> plt.plot(x, y2)
[<matplotlib.lines.Line2D object at 0x111e2dc88>]
>>> plt.ylim(-0.1, 1.1) # specify y range
(-0.1, 1.1)
>>> plt.show()
Fig. 3-8 Step Function (dashed line) and Sigmoid Function
Like a dashed line above, neural network can handle with continuous real numbers as signals.
Both functions return smaller number (zero for the step function) when an input is smaller; they return larger number (one for the step function) when an input is larger. Also, no matter how small or large an input number is, an output from each function is between 0 and 1.
[3.2.6] Non-Linear Function
Both step function and sigmoid function are non-linear functions. In neural network, an activation function has to be non-linear. Why? Because it is non-sense if we use a linear function to have multi-layered neutral network; we can realize that by using one linear function. (e.g., a linear function h(x) = cx, y(x) = h(h(h(x)))) = c3 * x, then y(x) = ax, c3 = a. It can be expressed without a hidden layer.)
Therefore, to capitalize on multi-layering, an activation function has to be non-linear.
[3.2.7] ReLU Function
ReLU: Rectified Linear Unit
h(x) = x (x > 0), 0 (x <= 0) (3.7)
If an input is larger than zero, then input = output; if an input is equal to, or smaller than, zero, then output = 0.
>>> import numpy as np
>>> import matplotlib.pylab as plt
>>>
>>> def relu(x):
... return np.maximum(0, x)
...
>>> x = np.arange(-6.0, 6.0, 0.1)
>>> y = relu(x)
>>> plt.plot(x, y)
[<matplotlib.lines.Line2D object at 0x112b24d68>]
>>> plt.ylim(-1, 6)
(-1, 6)
>>> plt.show()
Fig. 3-9 ReLU function
[3.3] Multi-Dimension Array Calculation
If you master calculations of NumPy multi-dimension arrays, it would be efficient to implement neural network.
[3.3.1] Multi-Dimension Array
A multi-dimension array could have numbers in one line (1-dimension), 2-dimension, 3-dimension, or N-dimension.
A one dimension array:
>>> import numpy as np
>>> A = np.array([1, 2, 3, 4])
>>> print(A)
[1 2 3 4]
>>> np.ndim(A)
1
>>> A.shape
(4,)
>>> A.shape[0]
4
A two-dimension array (aka matrix):
>>> B = np.array([[1, 2],[3, 4],[5, 6]])
>>> print(B)
[[1 2]
[3 4]
[5 6]]
>>> np.ndim(B)
2
>>> B.shape
(3, 2)
>>> B.shape[0]
3
>>> B.shape[1]
2
[3.3.2] Inner Product of Matrix
>>> A = np.array([[1, 2],[3, 4]])
>>> A.shape
(2, 2)
>>> B = np.array([[5, 6],[7, 8]])
>>> B.shape
(2, 2)
>>> np.dot(A, B)
array([[19, 22],
[43, 50]])
Calculation of a matrix AB goes like this:
row 1, column 1: 1*5 + 2*7 = 19
row 1, column 2: 1*6 + 2*8 = 22
row 1, column 1: 3*5 + 4*7 = 43
row 1, column 1: 3*6 + 4*8 = 50
>>> np.dot(B, A)
array([[23, 34],
[31, 46]])
As you can see above, the following matrix equation is not necessarily true: AB = BA
Computing an inverse matrix A-1 goes like this:
>>> np.linalg.inv(A)
array([[-2. , 1. ],
[ 1.5, -0.5]])
By definition, when a matrix A =
array([[a, b],
[c, d]])
then an inverse matrix A-1 is 1/(ad-bc) times
array([[d, -b],
[-c, a]])
In the case of A above,
a = 1, b = 2, c = 3, d = 4
1/(ad-bc) = 1/(1*4-2*3) = 1/(-2) = -0.5
A-1 =
array([[-0.5*4, -0.5*(-2)],
[-0.5*(-3), -0.5*1]])
=
array([[-2, 1],
[1.5, -0.5]])
>>> np.dot(A, np.linalg.inv(A))
array([[ 1.00000000e+00, 1.11022302e-16],
[ 0.00000000e+00, 1.00000000e+00]])
>>> np.dot(np.linalg.inv(A), A)
array([[ 1.00000000e+00, 4.44089210e-16],
[ 0.00000000e+00, 1.00000000e+00]])
To have integers, round can be used:
>>> np.round(np.dot(A, np.linalg.inv(A)), decimals=16)
array([[ 1.00000000e+00, 1.00000000e-16],
[ 0.00000000e+00, 1.00000000e+00]])
>>> np.round(np.dot(A, np.linalg.inv(A)), decimals=15)
array([[ 1., 0.],
[ 0., 1.]])
>>> np.round(np.dot(A, np.linalg.inv(A)), decimals=2)
array([[ 1., 0.],
[ 0., 1.]])
>>> np.dot(A, np.linalg.inv(A)).astype(np.int) # int does not work
array([[0, 0],
[0, 1]])
You can compute an inner product of i * j matrix A and j * k matrix B in this order. The number of columns for the first matrix (j) has to be equal to the number of rows for the second matrix (j). AB is an i*k matrix.
>>> A = np.array([[1, 2, 3],[4, 5, 6]])
>>> A.shape
(2, 3)
>>> B = np.array([[1, 2],[3, 4], [5, 6]])
>>> B.shape
(3, 2)
>>> np.dot(A, B)
array([[22, 28],
[49, 64]])
>>> C = np.array([[1, 2],[3, 4]])
>>> C.shape
(2, 2)
>>> A.shape
(2, 3)
>>> np.dot(A, C)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: shapes (2,3) and (2,2) not aligned: 3 (dim 1) != 2 (dim 0)
>>> np.dot(C, A)
array([[ 9, 12, 15],
[19, 26, 33]])
>>> A = np.array([[1, 2],[3, 4], [5, 6]])
>>> A.shape
(3, 2)
>>> B = np.array([7, 8])
>>> B.shape
(2,)
>>> np.dot(A, B)
array([23, 53, 83])
[3.3.2] Inner Product of Neural Network
>>> X = np.array([1, 2]) # x1 = 1, x2 = 2
>>> X.shape
(2,)
>>> print(X)
[1 2]
>>> W = np.array([[1, 3, 5],[2, 4, 6]])
>>> print(W)
[[1 3 5]
[2 4 6]]
>>> W.shape
(2, 3)
>>> Y = np.dot(X,W)
>>> print(Y) # y1 = 5, y2 = 11, y3 = 17
[ 5 11 17]
X =
[x1 x2]
W =
[[w1 w3 w5]
[w2 w4 w6]]
Y = XW =
[x1*w1+x2*w2 x1*w3+x2*w4 x1*w5+x2*w6] =
[y1 y2 y3]
X =
[1 2]
W =
[[1 3 5]
[2 4 6]]
Y = XW =
[1*1+2*2 1*3+2*4 1*5+2*6] =
[5 11 17]
[3.4] Implementing 3-layer Neural Network
A 3-layer neural network has (1) input layer, (2) first hidden layer, (3) second hidden layer, and (4) output layer. (1) consists of two neurons, (2) consists of three neurons, (3) consists of two neurons, and (4) consists of two neurons.
[3.4.1] Signs
Assume there are two neurons in (1) input layer, i.e., x1 and x2. Three neurons in (2) first hidden layer are
a1(1), a2(1), and a3(1). Weights can be written as follows:
wi j(n)
i: i-th neuron of the next layer
j: j-th neuron of the previous layer
n: n-th weighting
[3.4.2] Implementing Signal Transmission in Each Layer
a1(1) = b1(1) * 1 + (w1 1(1) * x1) + (w1 2(1) * x2) (3.8)
Bias b has only one index on the right hand side, bottom, because there is only one bias neuron.
If we use inner product of matrix, then (2) first hidden layer, a first layer, can be expressed as follows:
A(1) = B(1) + XW(1) (3.9)
A(1) = (a1(1), a2(1), a3(1))
B(1) = (b1(1), b2(1), b3(1))
X = (x1, x2)
W(1) = [ (w1 1(1), w2 1(1), w3 1(1)), (w1 2(1), w2 2(1), w3 2(1))]
>>> X = np.array([1.0, 0.5])
>>> W1 = np.array([[0.1, 0.3, 0.5],[0.2, 0.4, 0.6]])
>>> B1 = np.array([0.1, 0.2, 0.3])
>>>
>>> print(X.shape)
(2,)
>>> print(W1.shape)
(2, 3)
>>> print(B1.shape)
(3,)
>>>
>>> A1 = np.dot(X, W1) + B1
X has two numbers; it is given here.
B1 has three numbers because A(1) = (a1(1), a2(1), a3(1)), (2) hidden layer, has three values.
W1 has 2 * 3 numbers because X has two values X = (x1, x2) and A(1) = (a1(1), a2(1), a3(1)), (2) first hidden layer, has three components.
>>> def sigmoid(x):
... return 1 / (1 + np.exp(-x)) # h(x) = 1 / (1 + exp(-x))
...
>>> Z1 = sigmoid(A1)
>>> print(A1)
[ 0.3 0.7 1.1]
>>> print(Z1)
[ 0.57444252 0.66818777 0.75026011]
z1(1), output of (2) hidden layer, is defined as follows:
z1(1) = sigmoid(a1(1))
a1(1) = b1(1) + w1 1(1) x1 + w1 2(1) x2
-----
Let's move on to the implementation from (2) first hidden layer to (3) second hidden layer.
>>> W2 = np.array([[0.1, 0.4],[0.2, 0.5], [0.3, 0.6]])
>>> B2 = np.array([0.1, 0.2])
>>>
>>> print(Z1.shape)
(3,)
>>> print(W2.shape)
(3, 2)
>>> print(B2.shape)
(2,)
>>> A2 = np.dot(Z1, W2) + B2
>>> Z2 = sigmoid(A2)
Similarly, the implementation from (3) second hidden layer to (4) output layer is:
>>> def identity_function(x):
... return x
...
>>> W3 = np.array([[0.1, 0.3],[0.2, 0.4]])
>>> B3 = np.array([0.1, 0.2])
>>>
>>> A3 = np.dot(Z2, W3) + B3
>>> Y = identity_function(A3) # or Y = A3
An activation function in (4) output layer is expressed by σ() to differentiate it from other activation functions in hidden layers of (2) and (3). How to choose σ() depends on a nature of the problem to be solved. For a regression, it is generally identity function. For 2-class classification, it's sigmoid. For multi-class classification, it is a softmax function.
[3.4.3] Summary of Neural Network Implementation
>>> def init_network():
... network = {}
... network['W1'] = np.array([[0.1, 0.3, 0.5],[0.2, 0.4, 0.6]])
... network['b1'] = np.array([0.1, 0.2, 0.3])
... network['W2'] = np.array([[0.1, 0.4],[0.2, 0.5],[0.3, 0.6]])
... network['b2'] = np.array([0.1, 0.2])
... network['W3'] = np.array([[0.1, 0.3],[0.2, 0.4]])
... network['b3'] = np.array([0.1, 0.2])
... return network
...
>>> def forward(network, x):
... W1, W2, W3 = network['W1'], network['W2'], network['W3']
... b1, b2, b3 = network['b1'], network['b2'], network['b3']
... a1 = np.dot(x, W1) + b1
... z1 = sigmoid(a1)
... a2 = np.dot(z1, W2) + b2
... z2 = sigmoid(a2)
... a3 = np.dot(z2, W3) + b3
... y = identity_function(a3)
... return y
...
>>> network = init_network()
>>> x = np.array([1.0, 0.5])
>>> y = forward(network, x)
>>> print(y)
[ 0.31682708 0.69627909]
init_network() does the initialization of weights and biases. The output of it (a series of weights and biases that are necessary for each layer) is stored to a variable network.
forward() implements processes for input signal conversions to an output signal. forward means a direction from input to output. backward is opposite.
[3.5] Designing Output Layer
[3.5.1] Identity Function and Softmax Function
Neural network can be used for both classification and regression, but you need to choose an appropriate activation function accordingly. Generally speaking, a softmax function is for classifications (specifying a classification for a given input) and an identity function for regressions (estimating a certain number).
Identify function:
a1 -- σ() --> y1
a2 -- σ() --> y2
a3 -- σ() --> y3
Softmax function:
yk = exp(ak) / Σi=1n exp(ai) (3.10)
exp(x) = ex
exp(1) = e1 = 2.71828...
n: number of outputs
yk: k-th output
a1, a2, a3 -- σ() --> y1
a1, a2, a3 -- σ() --> y2
a1, a2, a3 -- σ() --> y3
>>> a = np.array([0.3, 2.9, 4.0])
>>> exp_a = np.exp(a)
>>> print(exp_a)
[ 1.34985881 18.17414537 54.59815003]
>>> sum_exp_a = np.sum(exp_a)
>>> print(sum_exp_a)
74.1221542102
>>> y = exp_a / sum_exp_a
>>> print(y)
[ 0.01821127 0.24519181 0.73659691]
Softmax function is defined as follows:
>>> def softmax(a):
... exp_a = np.exp(a)
... sum_exp_a = np.sum(exp_a)
... y = exp_a / sum_exp_a
... #
... return y
...
>>>
[3.5.2] A Problem When Implementing a Softmax Function
Exponential figures easily get large numbers.
>>> import numpy as np
>>> np.exp(10)
22026.465794806718
>>> np.exp(100)
2.6881171418161356e+43
>>> np.exp(1000)
__main__:1: RuntimeWarning: overflow encountered in exp
inf
Softmax function (3.10) can be modified to avoid an overflow problem above as follows:
yk = exp(ak) / Σi=1n exp(ai)
= C * exp(ak) / {C * Σi=1n exp(ai)}
= exp(ln(C)) * exp(ak) / {exp(ln(C)) * Σi=1n exp(ai)}
= exp(ak + ln(C)) / Σi=1n exp(ai + ln(C)) (3.11)
= exp(ak + C') / Σi=1n exp(ai + C')
ln(x) = loge(x) = y = ln(exp(y))
x = exp(y) = exp(ln(x))
Therefore, C = exp(ln(C))
Also, ln(C) = C'
What (3.11) means is that you can add (subtract) any number to (from) both numerator and denominator. In this case, it's C'. To avoid an overflow problem, C' is usually set to the maximum number within the inputs.
>>> a = np.array([1010, 1000, 990])
>>> a
array([1010, 1000, 990])
>>> np.exp(a) / np.sum(np.exp(a)) # softmax function calculation
array([ nan, nan, nan])
>>> # It is not calculated propoerly.
...
>>> c = np.max(a) #1010
>>> a - c
array([ 0, -10, -20])
>>> np.exp(a - c) / np.sum(np.exp(a - c)) # softmax function calculation
array([ 9.99954600e-01, 4.53978686e-05, 2.06106005e-09])
Finally, Softmax function implementation with an overflow prevention goes like this:
>>> def softmax(a):
... c = np.max(a)
... exp_a = np.exp(a - c) # overflow prevention
... sum_exp_a = np.sum(exp_a)
... y = exp_a / sum_exp_a
... return y
...
>>>
[3.5.3] Features of Softmax Function
If you use the softmax() defined above, a neural network output can be calculated as follows:
>>> a = np.array([0.3, 2.9, 4.0])
>>> y = softmax(a)
>>> print(y)
[ 0.01821127 0.24519181 0.73659691]
>>> np.sum(y)
1.0
As shown above, an output from a softmax function is a real number and varies from zero to one. Also, the sum of outputs is one; that is, an output from a softmax function is regarded as a probability.
Moreover, a softmax function in an output layer can be omitted because softmax (and exp) would not change magnitude relationships among outputs; the biggest number always gets the highest probability, because exp is a monotonically increasing function.
There are two phases in a deep learning: learning and inference (classification)
First, learning of a model is done. Second, in the inference phase, the model is used to infer by using unknown (out of sample) data. As described above, a softmax function in an output layer in the inference phase is usually omitted.
[3.5.4] A Number of Neurons in an Output Layer
A number of neurons in an output layer is usually set to the number of classifications; for example, if you want to classify an input image into numbers from zero to nine (10 classifications), then outputs in an output layer should be ten, i.e., y0, y1, ..., and y9. If y2 has the biggest number, then this neural network forecasts 2 as a plausible output.
[3.6] Recognition of Hand-Written Numbers
Please consider that the learning is done. By using parameters learned, we're going to implement an inference process (aka forward propagation) here.
[3.6.1] MNIST Data Set
>>> import sys, os
>>> os.getcwd() # show your current directory
>>> sys.path # show your system path
We are going to use mnist.py, which supports MNIST data set downloading and image data conversion to a NumPy array. There should be mnist.py in the dataset directory if you download files in the section [0] Prep. You have to be in a directory of ch01, ch02, or ch08 when you use the mnint.py.
>>> os.chdir(path) # a path to ch03, for instance, depends on your environment
>>> os.getcwd()
>>> import sys, os
>>> sys.path.append(os.pardir) # import files in a parent directory
>>> from dataset.mnist import load_mnist # load_mnist() function in dataset/mnist.py
>>> # It takes a few minutes for the first time.
... (x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
Downloading train-images-idx3-ubyte.gz ...
Done
Downloading train-labels-idx1-ubyte.gz ...
Done
Downloading t10k-images-idx3-ubyte.gz ...
Done
Downloading t10k-labels-idx1-ubyte.gz ...
Done
Converting train-images-idx3-ubyte.gz to NumPy Array ...
Done
Converting train-labels-idx1-ubyte.gz to NumPy Array ...
Done
Converting t10k-images-idx3-ubyte.gz to NumPy Array ...
Done
Converting t10k-labels-idx1-ubyte.gz to NumPy Array ...
Done
Creating pickle file ...
Done!
>>> # ouput each data shape
>>> print(x_train.shape) #(60000, 784)
(60000, 784)
>>> print(t_train.shape) #(60000, )
(60000,)
>>> print(x_test.shape) #(10000, 784)
(10000, 784)
>>> print(t_test.shape) #(10000, )
(10000,)
load_mnist() returns "(training image, training label), (test image, test label)" by using the loaded MNIST data.
If you look at:
load_mnist(normalize=True, flatten=True, one_hot_label=False)
normalize=True
means standardization (0.0 to 1.0) by using the input image
normalize=False
means no standardization, i.e., (0 to 255), an input image gets unchanged
flatten=True
stored as a one-dimension array with 784 components
flatten=False
stored as a three-dimension array with 1x28x28 components
one_hot_label=True
stored as an array with labels many 0s and only one 1 (correct answer)
one_hot_label=False
stored as an array only with correct labels e.g., 7, 2
You can find a script with the following code in ch03/mnist_show.py.
>>> import sys, os
>>> sys.path.append(os.pardir) # import files in a parent directory
>>> import numpy as np
>>> from dataset.mnist import load_mnist
>>> from PIL import Image
>>>
>>> def img_show(img):
... pil_img = Image.fromarray(np.uint8(img)) # data conversion from NumPy array to PIL (Python Image Library) data object
... pil_img.show()
...
>>> (x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False) # flatten=True makes an image one-dimension NumPy array
>>> img = x_train[0]
>>> label = t_train[0]
>>> print(label) #5
5
>>>
>>> print(img.shape)
(784,)
>>> img = img.reshape(28, 28) # reshape to the original image size
>>> print(img.shape)
(28, 28)
>>> img_show(img)
[3.6.2] Inference Process in Neural Network
Let's implement a neural network which does an inference processing for the MNIST data set. The neural network consists of 784 neurons (=28*28 pixels of an image file) in an input layer and 10 neurons (classifications from 0 to 10) in an output layer. Also, there are two hidden layers; the first has 50 and the second has 100 neurons in this case. The number 50 or 100 are arbitrary - you can choose whatever you want.
First off, change your current directory.
>>> import sys, os
>>> os.getcwd() # show your current directory
>>> sys.path # show your system path
You have to be in a directory of ch01, ch02, or ch08.
>>> os.chdir(path) # a path to ch03, for instance, depends on your environment
>>> os.getcwd()
>>> import sys, os
>>> sys.path.append(os.pardir) # import files in a parent directory
>>> import numpy as np
>>> from dataset.mnist import load_mnist
>>> from PIL import Image
You can find a script with the following code in ch03/nueralnet_mnist.py.
>>> def get_data():
... (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False) # normalize=True is normalization, a pre-processing process
... return x_test, t_test
...
>>> def init_network():
... with open("sample_weight.pkl", 'rb') as f:
... network = pickle.load(f)
... return network
...
>>> def predict(network, x):
... W1, W2, W3 = network['W1'], network['W2'], network['W3']
... b1, b2, b3 = network['b1'], network['b2'], network['b3']
... a1 = np.dot(x, W1) + b1
... z1 = sigmoid(a1)
... a2 = np.dot(z1, W2) + b2
... z2 = sigmoid(a2)
... a3 = np.dot(z2, W3) + b3
... y = softmax(a3)
... return y
>>> x, t = get_data()
>>> import pprint, pickle
>>> network = init_network()
>>> accuracy_cnt = 0
>>> for i in range(len(x)):
... y = predict(network, x[i])
... p = np.argmax(y) # an index with the highest probability
... if p == t[i]:
... accuracy_cnt += 1
>>> print("Accuracy:" + str(float(accuracy_cnt)/len(x)))
The result above will be:
Accuracy:0.9352
This means the classification with 93.52% accuracy.
Instead of writing each line of script, you can execute ch03/neuralnet_mnist.py on Terminal of MacOS (or cmd on Windows).
$ python neuralnet_mnist.py
Accuracy:0.9352
[3.6.3] Batch Processing
>>> x, _ = get_data()
>>> network = init_network()
>>> W1, W2, W3 = network['W1'], network['W2'], network['W3']
>>> x.shape
(10000, 784)
>>> x[0].shape
(784,)
>>> W1.shape
(784, 50)
>>> W2.shape
(50, 100)
>>> W3.shape
(100, 10)
Please make sure that dimensions of arrays are matched.
Fig. 3-26 Array Shapes
X W1 W2 W3 Y
784 784x50 50x100 100x10 10
When we have many images as inputs, such as, 100 images, then X would be 100x784 as an aggregated input.
Fig. 3-27 Array Shapes in a Batch Processing
X W1 W2 W3 Y
100x784 784x50 50x100 100x10 100x10
Let's implement a batch processing here.
>>> x, t = get_data()
>>> network = init_network()
>>>
>>> batch_size = 100 # size of batch
>>> accuracy_cnt = 0
>>>
>>> for i in range(0, len(x), batch_size):
... x_batch = x[i:i+batch_size]
... y_batch = predict(network, x_batch)
... p = np.argmax(y_batch, axis=1)
... accuracy_cnt += np.sum(p == t[i:i+batch_size])
...
>>>
>>> print("Accuracy:" + str(float(accuracy_cnt)/len(x)))
Accuracy:0.9352
range(start, end) is a list of integers from start to (end-1).
range(start, end, step) is a list of integers from start with an increase by step until (end-1).
>>> list(range(0, 10))
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> list(range(0, 10, 3))
[0, 3, 6, 9]
>>> list(range(0, 10, 5))
[0, 5]
>>> x = np.array([[0.1, 0.8, 0.1], [0.3, 0.1, 0.6], [0.2, 0.5, 0.3], [0.8, 0.1, 0.1]])
>>> y = np.argmax(x, axis=1) # argmax returns an index that contains the max number
>>> print(y)
[1 2 1 0]
>>> y = np.array([1, 2, 1, 0])
>>> t = np.array([1, 2, 0, 0])
>>> print(y == t)
[ True True False True]
>>> np.sum(y == t)
3
[3.7] Summary
- We review forward propagations of neural network in this chapter. In neural network, we use a sigmoid function which smoothly change outputs as an activation function. On the contrary, in perceptron, a step function which changes output from 0 to 1 without smoothing is used as an activation function.
- NumPy multi-dimension arrays can be used to implement a neutral network in an efficient manner.
- Problems to be solved by machine learning can be classified into regression and classification.
- An activation function in an output layer is usually (A) an identify function for regression or (B) a softmax function for classification.
- For classification, the number of neurons in an output layer is set to the number of classifications.
- A set of input data is called batch; inference processing for each batch unit makes calculations faster.
[4] Learning in Neural Network
We introduce a loss function here. We try to find weight parameters that make the loss function value minimum. We use gradient (descent) method, which uses a slope of the function.
[4.1] Learning by Data
The feature of neural network is learning by data, namely, weight parameters can be automatically chosen by data. We are going to implement learning hand-written numbers of MNIST data set.
[4.1.1] Data Driven
A feature quality (amount of characteristic of an image) is a designed converter that properly extract output of intrinsic data from input data (images). A pattern of the feature quantity can be learned by machine learning techniques. An image data can be converted to vectors by using a feature quantity. However, the feature quantity has to be chosen or newly created by a human in a typical machine learning excluding deep learning.
Fig. 4-2
Image file --> (algorithm by a human) --> answer
Image file --> (feature quantity by a human) --> (machine learning like SVM, KNN) --> answer
Image file --> (neural network / deep learning or end-to-end machine learning) --> answer
No human intervention is indicated by bold characters.
[4.1.2] Training Data and Test Data
In machine learning, training data (sample data, teacher data) is used to specify a model with the best parameters first. Second, the trained model is tested by using test data (out-of-sample data). By this, we evaluate a general aptitude of the model. If you optimize the model only for sample data and the model does not work for out-of-sample data, then the model is in an overfitting problem. Avoiding overfitting is important in machine learning.
[4.2] Loss Function
A loss function in neural network learning is an index that evaluate how "bad" the neural network's ability is. Minimizing the loss function is maximizing the ability of the model.
[4.2.1] Mean Squared Error
One of the most famous loss functions is a mean squared error.
E = (1/2) * Σk exp(yk - tk)2 (4.1)
yk : neural network output
tk : training (teacher) data
k : dimension of data
>>> def mean_squared_error(y, t):
... return 0.5 * np.sum((y-t)**2)
...
>>>
... # [2], the third component, is a right answer
...
>>> t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
>>>
>>> # Example 1: [2] has the highest probability (0.6)
... y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
>>>
>>> mean_squared_error(np.array(y), np.array(t))
0.097500000000000031
>>>
>>> # Example 2: [7] has the highest probability (0.6)
... y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
>>> mean_squared_error(np.array(y), np.array(t))
0.59750000000000003
As you can see above, the first loss function has smaller number (0.097500000000000031) and error. That is, the first example shows that outputs are well matched with training (teacher) data.
[4.2.2] Cross Entropy Error
E = -Σk tk * loge(yk) (4.2)
yk : neural network output
tk : training (teacher) data, correct answer label (one-hot expression with only one 1 and other 0s)
k : dimension of data
>>> np.log(0.6)
-0.51082562376599072
>>> np.log(0.1)
-2.3025850929940455
>>>
>>> t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
>>> y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
>>> cross_entropy_error(np.array(y), np.array(t))
0.51082545709933802
>>>
>>> y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
>>> cross_entropy_error(np.array(y), np.array(t))
2.3025840929945458
The first is better.
[4.2.3] Mini-batch Learning
If there are N training data, (4.2) can be written as follows.
E = -(1/N)Σn Σk tnk * loge(ynk) (4.3)
ynk : neural network output, n-th data, dimension k
tnk : training (teacher) data, correct answer label (one-hot expression with only one 1 and other 0s), n-th data, dimension k
n: n-th data
k : dimension of data
When learning in neutral network, each mini-batch (small chunk) of training data is chosen and learned.
Loading MNIST data set (dataset/mnist.py):
>>> import sys, os
>>> sys.path.append(os.pardir)
>>> import numpy as np
>>> from dataset.mnist import load_mnist
>>>
>>> (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
>>>
>>> print(x_train.shape) # 60,000 training data, 784(28x28)-dimension input data
(60000, 784)
>>> print(t_train.shape) # 10-dimension teacher data
(60000, 10)
Randomly choose 10 data from the training data.
>>> train_size = x_train.shape[0]
>>> train_size
60000
>>> batch_size = 10
>>> batch_mask = np.random.choice(train_size, batch_size)
>>> batch_mask
array([ 4957, 9951, 7070, 21607, 47857, 58590, 42236, 3033, 25998, 17251])
>>> x_batch = x_train[batch_mask]
>>> t_batch = t_train[batch_mask]
>>>
[4.2.4] Mini-batch Learning Implementation: Cross Entropy Error
>>> def cross_entropy_error(y, t):
... if y.ndim == 1:
... t = t.reshape(1, t.size)
... y = y.reshape(1, y.size)
... batch_size = y.shape[0]
... return -np.sum(t * np.log(y)) / batch_size
...
>>>
y: output of neural network
t: teacher data
If teacher data is given as a label, e.g., 2 or 7, not one-hot expression 0 or 1, then
>>> def cross_entropy_error(y, t):
... if y.ndim == 1:
... t = t.reshape(1, t.size)
... y = y.reshape(1, y.size)
... batch_size = y.shape[0]
... return -np.sum(np.log(y[np.arrange(batch_size), t])) / batch_size # different from the one above
...
>>>
[4.2.5] Why Loss Function?
If you look at a Sigmoid function, its differential is not zero anywhere. It is a very important feature to find the best parameters.
[4.3] Numerical Differentiation
[4.3.1] Differentiation
Definition of analytic differentiation:
df(x) / dx = lim h --> 0 {f(x+h) - f(x)} / h (4.4)
>>> def numerical_diff(f, x):
... h = 1e-4 #0.0001
... return (f(x+h) - f(x-h)) / (2*h)
...
>>>
[4.3.2] An Example of Numerical Differentiation
f(x) = y = 0.01x^2 + 0.1x (4.5)
>>> def function_1(x):
... return 0.01*x**2 + 0.1*x
...
>>>
Next, draw the function y = f(x) above.
>>> import numpy as np
>>> import matplotlib.pylab as plt
>>>
>>> x = np.arange(0.0, 20.0, 0.1) # x array, from 0 to 20, increase by 0.1
>>> y = function_1(x)
>>> plt.xlabel("x")
<matplotlib.text.Text object at 0x12939a630>
>>> plt.ylabel("f(x)")
<matplotlib.text.Text object at 0x1293b4cf8>
>>> plt.plot(x, y)
[<matplotlib.lines.Line2D object at 0x12956e1d0>]
>>> plt.show()
>>> numerical_diff(function_1, 5)
0.1999999999990898
>>> numerical_diff(function_1, 10)
0.2999999999986347
df(x) / dx = 0.02x + 0.1
>>> 0.02 * 5 + 0.1
0.2
>>> 0.02 * 10 + 0.1
0.30000000000000004
Errors are very small as you can see above and in the source code of ch04/gradient_1d.py.
[4.3.3] Partial Differentiation
f(x0, x1) = x0^2 + x1^2 (4.6)
Note that there are two types of variables. Or, by using X, Y, and Z, it can be written as follows.
Z = f(X, Y) = X^2 + Y^2 (4.6)'
>>> import numpy as np
>>> import matplotlib.pylab as plt
>>> from mpl_toolkits.mplot3d import Axes3D
>>> x = np.arange(-3.0, 3.0, 0.1)
>>> y = np.arange(-3.0, 3.0, 0.1)
>>> X, Y = np.meshgrid(x,y)
>>> print("x=", x)
>>> print("X=", X)
>>> print("y=", y)
>>> print("Y=", Y)
>>> def function_2(X, Y):
... return X**2 + Y**2
...
>>>
>>> Z = function_2(X, Y)
>>> print("Z=", Z)
>>> fig = plt.figure()
>>> ax = Axes3D(fig)
>>> ax.plot_wireframe(X, Y, Z)
<mpl_toolkits.mplot3d.art3d.Line3DCollection object at 0x116bc22b0>
>>> ax.set_xlabel("X")
<matplotlib.text.Text object at 0x10d13b240>
>>> ax.set_ylabel("Y")
<matplotlib.text.Text object at 0x10d14cd30>
>>> ax.set_zlabel("Z")
<matplotlib.text.Text object at 0x10d15c748>
>>> plt.show()
Fig 4-8 Z = f(X, Y) = X^2 + Y^2
z = f(x, y) = x^2 + y^2
∂ f(x, y) / ∂x = 2 * x
∂ f(x, y) / ∂y = 2 * y
When x = 3, y = 4,
∂ f(x, y) / ∂x = 2 * x = 2 * 3 = 6
When x = 3, y = 4,
∂ f(x, y) / ∂y = 2 * y = 2 * 4 = 8
>>> def numerical_diff(f, x):
... h = 1e-4 #0.0001
... return (f(x+h) - f(x-h)) / (2*h)
...
>>>
>>> def function_tmp1(x):
... return x*x + 4.0**2.0
...
>>> numerical_diff(function_tmp1, 3.0)
6.00000000000378
>>> def function_tmp2(y):
... return 3.0**2.0 + y*y
...
>>> numerical_diff(function_tmp2, 4)
7.999999999999119
>>>
[4.4] Gradient
>>> import numpy as np
>>> def function_2(x):
... return x[0]**2 + x[1]**2
...
>>>
>>> def numerical_gradient(f,x):
... h = 1e-4 # 0.0001
... grad = np.zeros_like(x)
... #
... for idx in range(x.size):
... tmp_val = x[idx]
... # f(x+h) calculation
... x[idx] = tmp_val + h
... fxh1 = f(x)
... #
... # f(x-h) calculation
... x[idx] = tmp_val - h
... fxh2 = f(x)
... #
... grad[idx] = (fxh1 - fxh2) / (2*h)
... x[idx] = tmp_val
... #
... return grad
...
>>>
>>> numerical_gradient(function_2, np.array([3.0, 4.0]))
array([ 6., 8.])
>>> numerical_gradient(function_2, np.array([0.0, 2.0]))
array([ 0., 4.])
>>> numerical_gradient(function_2, np.array([3.0, 0.0]))
array([ 6., 0.])
You can draw Fig 4-9 by ch04/gradient_2d.py:
$ python gradient_2d.py
Fig 4-9 Gradients of f(x0, x1) = x0^2 + x1^2
[4.4.1] Gradient Method
In a gradient method, you continuously check a direction of a gradient and travel a constant distance in order to gradually lower a value of a loss function. (This is a gradient descent method and the opposite is a gradient ascent method.) It is a popular way in an optimization of machine learning.
Gradient method:
x0 = x0 - η ∂f / ∂x0
x1 = x1 - η ∂f / ∂x1
(4.7)
η: learning rate (quantity of an update; how much should it learn and update a parameter)
Gradient descent method:
>>> def gradient_descent(f, init_x, lr=0.01, step_num=100):
... x = init_x
... #
... for i in range(step_num):
... grad = numerical_gradient(f, x)
... x -= lr * grad
... #
... return x
...
>>>
f : a function to be optimized
init_x : initial value
lr : learning rate
step_num : number of steps
Question: What is the minimum value of f(x0, x1) = x0^2 + x1^2 ? Use a gradient method.
>>> def function_2(x):
... return x[0]**2 + x[1]**2
...
>>>
>>> init_x = np.array([-3.0, 4.0])
>>> gradient_descent(function_2, init_x=init_x, lr=1e-10, step_num=100)
array([-2.99999994, 3.99999992])
>>> init_x = np.array([-3.0, 4.0])
>>> gradient_descent(function_2, init_x=init_x, lr=0.01, step_num=100)
array([-0.39785867, 0.53047822])
>>> init_x = np.array([-3.0, 4.0])
>>> gradient_descent(function_2, init_x=init_x, lr=0.1, step_num=100)
array([ -6.11110793e-10, 8.14814391e-10])
>>> init_x = np.array([-3.0, 4.0])
>>> gradient_descent(function_2, init_x=init_x, lr=1, step_num=100)
array([-3., 4.])
>>> init_x = np.array([-3.0, 4.0])
>>> gradient_descent(function_2, init_x=init_x, lr=10, step_num=100)
array([ -2.58983747e+13, -1.29524862e+12])
A learning rate (lr) should not be too big or small. If it's too big, the results get bigger; if it's too small, the results get updated only a little bit. The most important thing for a human is to choose an appropriate learning rate (so-called hyper parameter). Hyper parameters have to be found by trial and error.
You can draw Fig 4-10 by ch04/gradient_method.py:
$ python gradient_method.py
Fig 4-10 Gradient method of f(x0, x1) = x0^2 + x1^2
[4.4.2] Gradient against neural network
References
[A] Learn Python Pro by Sololearn Inc
iPhone App for very basic Python programming
https://appsto.re/jp/mHh34.i
[B] Introducing Python: Modern Computing in Simple Packages 1st Edition
For basic Python programming
Amazon.com
Amazon.co.jp
[C] Python for Data Analysis: Data Wrangling with Pandas, NumPy, and IPython 2nd Edition
For NumPy
Amazon.com
Amazon.co.jp
[D] Scipy Lecture Notes
For NumPy and Matplotlib
http://www.scipy-lectures.org
Subscribe to:
Comments (Atom)
Deep Learning (Regression, Multiple Features/Explanatory Variables, Supervised Learning): Impelementation and Showing Biases and Weights
Deep Learning (Regression, Multiple Features/Explanatory Variables, Supervised Learning): Impelementation and Showing Biases and Weights ...
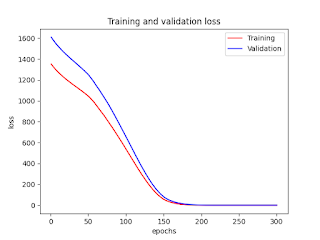
-
Black-Litterman Portfolio Optimization with Python This is a very basic introduction of the Black-Litterman portfolio optimization with t...
-
This is a great paper to understand having and applying principles to day-to-day business and personal lives. If you do not have your own ...
-
How to win friends & influence people: Part 1 (Influence people and let them move.) Principle 1: Don't criticize, condemn, or ...











