| # Install on Terminal of MacOS # 1. pandas #pip3 install -U pandas # 2. NumPy #pip3 install -U numpy # 3. matplotlib #pip3 install -U matplotlib # 4. scikit-learn (sklearn) #pip3 install -U scikit-learn # 5. tensorflow #pip3 install -U tensorflow |
1_MacOS_Terminal.txt
| ########## Run Terminal on MacOS and execute ### TO UPDATE cd "YOUR_WORKING_DIRECTORY" python3 dlregweights2.py 300 l1l2 0.0250 |
Input data files
train_data_raw.csv
1.0, 29.0
2.0, 28.0
4.0, 26.0
5.0, 25.0
7.0, 23.0
8.0, 22.0
10.0, 20.0
11.0, 19.0
13.0, 17.0
14.0, 16.0
16.0, 14.0
17.0, 13.0
19.0, 11.0
20.0, 10.0
22.0, 8.0
23.0, 7.0
25.0, 5.0
26.0, 4.0
28.0, 2.0
29.0, 1.0
train_targets_raw.csv
-55.5
-51.5
-43.5
-39.5
-31.5
-27.5
-19.5
-15.5
-7.5
-3.5
4.5
8.5
16.5
20.5
28.5
32.5
40.5
44.5
52.5
56.5
test_data_raw.csv
0.0, 30.0
3.0, 27.0
6.0, 24.0
9.0, 21.0
12.0, 18.0
15.0, 15.0
18.0, 12.0
21.0, 9.0
24.0, 6.0
27.0, 3.0
30.0, 0.0
test_targets_raw.csv
-59.5
-47.5
-35.5
-23.5
-11.5
0.5
12.5
24.5
36.5
48.5
60.5
Python files
dlregweights2.py
#################### Deep Learning (Regression, Multiple Features/Explanatory Variables, Supervised Learning): Impelementation and Showing Biases and Weights ####################
########## How to run this code
#
# You can run this code on your MacOS Terminal (or other terminals) as follows:
#
# python3 dlregweights2.py 300 l1l2 0.0250
# python3 dlregweights2.py (num_epochs: number of epochs) (regl1l2: regularization) (regl1l2f: learning rate of regularization)
########## import sys
import sys
########## Argument(s)
#num_epochs = 10000
num_epochs = int(sys.argv[1])
#regl1l2 = 'None'
#regl1l2 = 'l1l2'
regl1l2 = str(sys.argv[2])
#regl1l2f = 0.001
regl1l2f = float(sys.argv[3])
#dropout_rate = 0
#dropout_rate = float(sys.argv[4])
########## import others
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras import Model
from tensorflow.keras import regularizers
from tensorflow.keras.layers import Conv2D
from tensorflow.keras.layers import Flatten
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import BatchNormalization
from tensorflow.keras.layers import Layer
from tensorflow.keras.layers import Dropout
print(tf.__version__)
#2.3.0
########## Loading raw data (before standardization)
# In this simple training and test data, there is a following relationship:
# y (target: dependent variable) = 0.5 + 2.0 * x1 (data: independent variable 1) - 2.0 * x2 (data: independent variable 2)
train_data_raw = np.loadtxt('train_data_raw.csv', dtype='float64', delimiter=',')
'''
1.0, 29.0
2.0, 28.0
4.0, 26.0
5.0, 25.0
7.0, 23.0
8.0, 22.0
10.0, 20.0
11.0, 19.0
13.0, 17.0
14.0, 16.0
16.0, 14.0
17.0, 13.0
19.0, 11.0
20.0, 10.0
22.0, 8.0
23.0, 7.0
25.0, 5.0
26.0, 4.0
28.0, 2.0
29.0, 1.0
'''
train_targets_raw = np.loadtxt('train_targets_raw.csv', dtype='float64', delimiter=',')
'''
-55.5
-51.5
-43.5
-39.5
-31.5
-27.5
-19.5
-15.5
-7.5
-3.5
4.5
8.5
16.5
20.5
28.5
32.5
40.5
44.5
52.5
56.5
'''
test_data_raw = np.loadtxt('test_data_raw.csv', dtype='float64', delimiter=',')
'''
0.0, 30.0
3.0, 27.0
6.0, 24.0
9.0, 21.0
12.0, 18.0
15.0, 15.0
18.0, 12.0
21.0, 9.0
24.0, 6.0
27.0, 3.0
30.0, 0.0
'''
test_targets_raw = np.loadtxt('test_targets_raw.csv', dtype='float64', delimiter=',')
'''
-59.5
-47.5
-35.5
-23.5
-11.5
0.5
12.5
24.5
36.5
48.5
60.5
'''
########## Standardization (data/features to have average = 0, standard deviation = 1)
sc = StandardScaler()
#train_data = sc.fit_transform(train_data_raw)
train_data = train_data_raw # no standardization in this case
np.savetxt('train_data.csv', train_data, fmt ='%.8f', delimiter=',')
#
print(train_data.shape)
#(20, 2)
#
print(train_data.shape[0])
#20
#
print(train_data.shape[1])
#2
train_targets = train_targets_raw
np.savetxt('train_targets.csv', train_targets, fmt ='%.8f', delimiter=',')
#test_data = sc.fit_transform(test_data_raw)
test_data = test_data_raw # no standardization in this case
np.savetxt('test_data.csv', test_data, fmt ='%.8f', delimiter=',')
test_targets = test_targets_raw
np.savetxt('test_targets.csv', test_targets, fmt ='%.8f', delimiter=',')
##### Regularization
#print(regl1l2)
#print(regl1l2f)
if regl1l2 == 'None':
rg = None
#
elif regl1l2 == 'l1':
rg = regularizers.l1(l1=regl1l2f) # L1 regularization
#
elif regl1l2 == 'l2':
rg = regularizers.l2(l2=regl1l2f) # L2 regularization
#
elif regl1l2 == 'l1l2':
rg = regularizers.l1_l2(l1=regl1l2f, l2=regl1l2f) # L1 & L2 regularization
#
else:
print('Error: The second argument should be None, l1, l2, or l1l2.')
exit()
########## Model
#all-node-connected network
'''
model = Sequential([
#Conv2D(1, (3, 3), padding='same', name='L0_conv2d', input_shape=(10, 10, 1)),
#Flatten(name='L1_flatten'),
#Dense(10, name='L2_dense', use_bias=False),
#Dense(1, name='L3_dense'),
#BatchNormalization(name='L4_bn')
#
#Dense(1, kernel_regularizer=rg, activation='relu', name='L0_dense', input_shape=(train_data.shape[1],)),
#Dense(2, kernel_regularizer=rg, activation='relu', name='L0_dense', use_bias=True, input_shape=(1,)),
Dense(1, kernel_regularizer=rg, activation='relu', name='L0_dense', use_bias=True, input_shape=(1,)),
Dropout(dropout_rate, name='L1_dropout'),
Dense(1, kernel_regularizer=rg, activation='relu', name='L2_dense', use_bias=True),
Dropout(dropout_rate, name='L3_dropout'),
Dense(1, name='L4_dense')
#Dense(1, activation='softmax', name='L4_dense')
])
'''
model = Sequential([
#Dense(1, kernel_regularizer=rg, activation='relu', name='L0_dense', use_bias=True, input_shape=(1,)),
#Use the following Dense when train_data and test_data have more-than-1 columns.
#Dense(1, kernel_regularizer=rg, activation='relu', name='L0_dense', use_bias=True, input_shape=(train_data.shape[1],)),
Dense(train_data.shape[1], kernel_regularizer=rg, activation='relu', name='L0_dense', use_bias=True, input_shape=(train_data.shape[1],)),
Dense(1, name='L1_dense')
])
model.summary()
'''
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
L0_dense (Dense) (None, 2) 6
_________________________________________________________________
L1_dense (Dense) (None, 1) 3
=================================================================
Total params: 9
Trainable params: 9
Non-trainable params: 0
_________________________________________________________________
'''
#exit()
########## Model Compiling: Regression
model.compile(optimizer='rmsprop', loss='mse', metrics=['mean_absolute_error'])
#
########## Model Compiling: Classification
#model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
########## Model Fitting and History Recording
history = model.fit( train_data,
train_targets,
validation_data=(test_data, test_targets),
epochs=num_epochs,
batch_size=1,
verbose=1) # Trains the model (in silent mode, verbose=0)
'''
...
Epoch 300/300
20/20 [==============================] - 0s 1ms/step - loss: 0.1729 - mean_absolute_error: 0.0533 - val_loss: 0.6400 - val_mean_absolute_error: 0.2446
'''
#print(history)
#<tensorflow.python.keras.callbacks.History object at 0x145d80490>
#print(history.history)
loss = history.history['loss']
val_loss = history.history['val_loss']
#
mae = history.history['mean_absolute_error']
val_mae = history.history['val_mean_absolute_error']
epochs = range(1, len(loss)+1)
########## Drawing figures
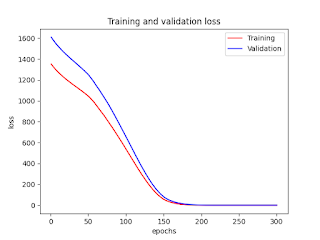
##### Loss
plt.plot(epochs, loss, 'r', label='Training')
plt.plot(epochs, val_loss, 'b', label='Validation')
plt.xlabel('epochs')
plt.ylabel('loss')
plt.title('Training and validation loss')
plt.legend()
plt.savefig('Fig_1_Loss.png')
plt.show()
##### MAE
plt.plot(epochs, mae, 'r', label='Training')
plt.plot(epochs, val_mae, 'b', label='Validation')
plt.xlabel('epochs')
plt.ylabel('MAE')
plt.title('Training and validation MAE')
plt.legend()
plt.savefig('Fig_2_MAE.png')
plt.show()
########## Model Evaluation by Test Data and Test Targets
model.evaluate(test_data, test_targets)
#1/1 [==============================] - 0s 285us/step - loss: 0.6400 - mean_absolute_error: 0.2446
########## Model Predictions by using Test Data
test_targets_pred = model.predict(test_data)
np.savetxt('test_targets_pred.csv', test_targets_pred, fmt ='%.8f', delimiter=',')
'''
-57.22531509
-47.47024155
-35.46761703
-23.46499062
-11.46236706
0.54025358
12.54287624
24.54549980
36.54811859
48.55074310
60.55336761
'''
########## Showing weights
print(len(model.layers))
#2
#exit()
l0 = model.layers[0]
l1 = model.layers[1]
##### Model Weights
print('##### Model Weights #####')
#model.weights has all the weights of all the layers.
print(model.weights)
'''
[<tf.Variable 'L0_dense/kernel:0' shape=(2, 2) dtype=float32, numpy=
array([[ 1.4862022 , 0.06257067],
[-0.06310117, 1.2727824 ]], dtype=float32)>, <tf.Variable 'L0_dense/bias:0' shape=(2,) dtype=float32, numpy=array([0.3552437, 1.0554012], dtype=float32)>, <tf.Variable 'L1_dense/kernel:0' shape=(2, 1) dtype=float32, numpy=
array([[ 1.46154 ],
[-1.4348773]], dtype=float32)>, <tf.Variable 'L1_dense/bias:0' shape=(1,) dtype=float32, numpy=array([-0.9223471], dtype=float32)>]
'''
#
#
print(type(model.weights))
# <class 'list'>
#
print(len(model.weights))
# 4
print(type(model.weights[0]))
#<class 'tensorflow.python.ops.resource_variable_ops.ResourceVariable'>
#
print(model.weights[0])
'''
<tf.Variable 'L0_dense/kernel:0' shape=(2, 2) dtype=float32, numpy=
array([[ 1.4862022 , 0.06257067],
[-0.06310117, 1.2727824 ]], dtype=float32)>
'''
#
print(model.weights[0].numpy())
'''
[[ 1.4862022 0.06257067]
[-0.06310117 1.2727824 ]]
'''
print(model.weights[1])
#<tf.Variable 'L0_dense/bias:0' shape=(2,) dtype=float32, numpy=array([0.3552437, 1.0554012], dtype=float32)>
#
print(model.weights[1].numpy())
#[0.3552437 1.0554012]
print(model.weights[2])
'''
<tf.Variable 'L1_dense/kernel:0' shape=(2, 1) dtype=float32, numpy=
array([[ 1.46154 ],
[-1.4348773]], dtype=float32)>
'''
#
print(model.weights[2].numpy())
'''
[[ 1.46154 ]
[-1.4348773]]
'''
print(model.weights[3])
#<tf.Variable 'L1_dense/bias:0' shape=(1,) dtype=float32, numpy=array([-0.9223471], dtype=float32)>
#
print(model.weights[3].numpy())
#[-0.9223471]
for w in model.weights:
print('{:<25}{}'.format(w.name, w.shape))
'''
L0_dense/kernel:0 (2, 2)
L0_dense/bias:0 (2,)
L1_dense/kernel:0 (2, 1)
L1_dense/bias:0 (1,)
'''
##### Layer 0
print('##### Layer 0: Dense #####')
print(l0.weights)
'''
[<tf.Variable 'L0_dense/kernel:0' shape=(2, 2) dtype=float32, numpy=
array([[ 1.4862022 , 0.06257067],
[-0.06310117, 1.2727824 ]], dtype=float32)>, <tf.Variable 'L0_dense/bias:0' shape=(2,) dtype=float32, numpy=array([0.3552437, 1.0554012], dtype=float32)>]
'''
for w in l0.weights:
print('{:<25}{}'.format(w.name, w.shape))
'''
L0_dense/kernel:0 (2, 2)
L0_dense/bias:0 (2,)
'''
### kernel
print(l0.weights[0])
'''
<tf.Variable 'L0_dense/kernel:0' shape=(2, 2) dtype=float32, numpy=
array([[ 1.4862022 , 0.06257067],
[-0.06310117, 1.2727824 ]], dtype=float32)>
'''
print(l0.weights[0].name)
#L0_dense/kernel:0
print(l0.weights[0].numpy())
'''
[[ 1.4862022 0.06257067]
[-0.06310117 1.2727824 ]]
'''
### bias
print(l0.weights[1])
#<tf.Variable 'L0_dense/bias:0' shape=(2,) dtype=float32, numpy=array([0.3552437, 1.0554012], dtype=float32)>
print(l0.weights[1].name)
#L0_dense/bias:0
print(l0.weights[1].numpy())
#[0.3552437 1.0554012]
##### Layer 1
#print('##### Layer 1: Dropout #####')
print('##### Layer 1: Dense #####')
print(l1.weights)
'''
[<tf.Variable 'L1_dense/kernel:0' shape=(2, 1) dtype=float32, numpy=
array([[ 1.46154 ],
[-1.4348773]], dtype=float32)>, <tf.Variable 'L1_dense/bias:0' shape=(1,) dtype=float32, numpy=array([-0.9223471], dtype=float32)>]
'''
for w in l1.weights:
print('{:<25}{}'.format(w.name, w.shape))
'''
L1_dense/kernel:0 (2, 1)
L1_dense/bias:0 (1,)
'''
### kernel
print(l1.weights[0])
'''
<tf.Variable 'L1_dense/kernel:0' shape=(2, 1) dtype=float32, numpy=
array([[ 1.46154 ],
[-1.4348773]], dtype=float32)>
'''
print(l1.weights[0].name)
#L1_dense/kernel:0
print(l1.weights[0].numpy())
'''
[[ 1.46154 ]
[-1.4348773]]
'''
### bias
print(l1.weights[1])
#<tf.Variable 'L1_dense/bias:0' shape=(1,) dtype=float32, numpy=array([-0.9223471], dtype=float32)>
print(l1.weights[1].name)
#L1_dense/bias:0
print(l1.weights[1].numpy())
#[-0.9223471]
########## Notes
# As described above, there is a following relationship in this simple training and test data:
# y (target: dependent variable) = 0.5 + 2.0 * x1 (data: independent variable 1) - 2.0 * x2 (data: independent variable 2)
# As you have already seen, the following weights are set as a result of deep learning optimization.
##### Layer 0
### kernel
#print(l0.weights[0].name)
#L0_dense/kernel:0
#print(l0.weights[0].numpy())
'''
[[ 1.4862022 0.06257067]
[-0.06310117 1.2727824 ]]
'''
### bias
#print(l0.weights[1].name)
#L0_dense/bias:0
#print(l0.weights[1].numpy())
#[0.3552437 1.0554012]
##### Layer 1
### kernel
#print(l1.weights[0].name)
#L1_dense/kernel:0
#print(l1.weights[0].numpy())
'''
[[ 1.46154 ]
[-1.4348773]]
'''
### bias
#print(l1.weights[1].name)
#L1_dense/bias:0
#print(l1.weights[1].numpy())
#[-0.9223471]
# By using these weights, we can derive the equation below:
# y (target: dependent variable) = 0.5 + 2.0 * x1 (data: independent variable 1) - 2.0 * x2 (data: independent variable 2)
#
# It goes like this:
#
# Layer 0:
# y0_0 = 0.3552437 + (1.4862022 * x1 - 0.06310117 * x2)
# y0_1 = 1.0554012 + (0.06257067 * x1 + 1.2727824 * x2)
#
# Layer 1:
# y = y1 = -0.9223471 + (1.46154) * y0_0 + (-1.4348773) * y0_1
#
# y = - 0.9223471
# + (1.46154) * y0_0
# + (-1.4348773) * y0_1
#
# = - 0.9223471
# + (1.46154) * { 0.3552437 + (1.4862022 * x1 - 0.06310117 * x2) }
# + (-1.4348773) * { 1.0554012 + (0.06257067 * x1 + 1.2727824 * x2) }
#
# = - 0.9223471
# + { (1.46154) * 0.3552437 + (1.46154) * (1.4862022 * x1 - 0.06310117 * x2) }
# + { (-1.4348773) * 1.0554012 + (-1.4348773) * (0.06257067 * x1 + 1.2727824 * x2) }
#
# = - 0.9223471
# + (1.46154) * 0.3552437 + (1.46154) * 1.4862022 * x1 + (1.46154) * (- 0.06310117) * x2
# + (-1.4348773) * 1.0554012 + (-1.4348773) * 0.06257067 * x1 + (-1.4348773) * 1.2727824 * x2
#
# = - 0.9223471
# + 0.519202877298 + 2.172143963388 * x1 + (-0.0922248840018) * x2
# -1.51437122427276 + (-0.089781234028791) * x1 + (-1.82628657359952) * x2
#
# = - 0.9223471 + 0.519202877298 -1.51437122427276
# + (2.172143963388 - 0.089781234028791) * x1
# + (-0.0922248840018 - 1.82628657359952) * x2
#
# = -1.91751544697476
# + (2.08236272935921) * x1
# + (-1.91851145760132) * x2
#
#
# Compare (1) calculated results by using this equation and (2) test_targets_pred: results of model.predict(test_data)
#
#test_data_raw
'''
0.0, 30.0
3.0, 27.0
6.0, 24.0
9.0, 21.0
12.0, 18.0
15.0, 15.0
18.0, 12.0
21.0, 9.0
24.0, 6.0
27.0, 3.0
30.0, 0.0
'''
#
# (1) calculated results by using this equation
'''
−1.91751544697476 + (2.08236272935921) * 0.0 + (−1.91851145760132) * 30.0
−1.91751544697476 + (2.08236272935921) * 3.0 + (−1.91851145760132) * 27.0
−1.91751544697476 + (2.08236272935921) * 6.0 + (−1.91851145760132) * 24.0
−1.91751544697476 + (2.08236272935921) * 9.0 + (−1.91851145760132) * 21.0
−1.91751544697476 + (2.08236272935921) * 12.0 + (−1.91851145760132) * 18.0
−1.91751544697476 + (2.08236272935921) * 15.0 + (−1.91851145760132) * 15.0
−1.91751544697476 + (2.08236272935921) * 18.0 + (−1.91851145760132) * 12.0
−1.91751544697476 + (2.08236272935921) * 21.0 + (−1.91851145760132) * 9.0
−1.91751544697476 + (2.08236272935921) * 24.0 + (−1.91851145760132) * 6.0
−1.91751544697476 + (2.08236272935921) * 27.0 + (−1.91851145760132) * 3.0
−1.91751544697476 + (2.08236272935921) * 30.0 + (−1.91851145760132) * 0.0
'''
'''
-59.47
-47.47
-35.47
-23.46
-11.46
0.54
12.54
24.55
36.55
48.55
60.55
'''
# (2) test_targets_pred
'''
-57.22531509
-47.47024155
-35.46761703
-23.46499062
-11.46236706
0.54025358
12.54287624
24.54549980
36.54811859
48.55074310
60.55336761
'''
#
#
# Thus,
# y ~ 0.50 + 2.00 * x1 - 2.00 *x2
Figures


No comments:
Post a Comment