The Financial Journal (Global): Python: Linear and Regularized Logistic Regression

0_runme.txt

##### Open Terminal on Mac OS

# Run the following commands on Terminal.

#Current working directory
pwd
#For instance, your MacOS environment goes like this:
#/Users/xxx/

#Change your working directory
#cd /Users/xxx/Downloads

which python3
#For instance, my MacOS environment goes like this:
#/Library/Frameworks/Python.framework/Versions/3.7/bin/python3

which pip3
#For instance, my MacOS environment goes like this:
#/Library/Frameworks/Python.framework/Versions/3.7/bin/pip3

#Run after connecting to the Internet
pip3 install matplotlib
pip3 install sklearn
pip3 install dtreeviz
pip3 install IPython

pip3 install pandas
pip3 install scipy

python3 -V
#For instance, my MacOS environment goes like this:
#Python 3.7.4

#Starting Python 3
#python3
#You do not use this since you're running py scripts on Terminal, rather than running your scripts on Pyton IDLE.

#Download files:
#ex1data1.txt
#ex1data2.txt
#ex2data1.txt
#ex2data2.txt
#
#From:
#https://github.com/LilianYe/Andrew-Ng-Machine-Learning-Programming-solutions-/find/master

#Running Python py scripts
python3 1a_liner_regression_w_one_variable.py
python3 1b_liner_regression_w_multiple_variables.py

python3 2.1_logistic_regression_or_classification.py
python3 2.2_regularized_logistic_regression.py

1a_liner_regression_w_one_variable.py

########## Python Implementation of Andrew Ng’s Machine Learning Course (Part 1)
########## Linear Regression with One Variable
#
# Reference:
#https://medium.com/analytics-vidhya/python-implementation-of-andrew-ngs-machine-learning-course-part-1-6b8dd1c73d80
#
#Here we will implement linear regression with one variable to predict profits for a food truck.
#
#ex1data1.txt
#contains the dataset for our linear regression exercise.
#column data
#1 population of a city
#2 profit of a food truck in that city

# import libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

###Reading and Plotting the data
data = pd.read_csv('ex1data1.txt', header = None) #read from dataset
X = data.iloc[:,0] # read first column
y = data.iloc[:,1] # read second column
m = len(y) # number of training example
data.head() # view first few rows of the data

plt.scatter(X, y)
plt.xlabel('Population of City in 10,000s')
plt.ylabel('Profit in $10,000s')
plt.savefig('fig_1a.1.png') # Save an image file
plt.show()

###Adding the intercept term
X = X[:,np.newaxis] #(*1)
y = y[:,np.newaxis] #(*1)
theta = np.zeros([2,1]) #set one initial parameter theta to 0
iterations = 1500
alpha = 0.01 # set another initial parameter, the learning rate alpha, to 0.01
ones = np.ones((m,1))
X = np.hstack((ones, X)) # adding the intercept term

#(*1)
#Note on np.newaxis:
# When you read data into X, you will observe that X, y are rank 1 arrays.
#rank 1 array will have a shape of (m, ) whereas rank 2 arrays will have a shape of (m,1).
#When operating on arrays its good to convert rank 1 arrays to rank 2 arrays because rank 1 arrays often give unexpected results.
#To convert rank 1 to rank 2 array we use someArray[:,np.newaxis].

###Computing the cost
def computeCost(X, y, theta):
temp = np.dot(X, theta) - y
return np.sum(np.power(temp, 2)) / (2*m)
J = computeCost(X, y, theta)
print(J)
#You should expect to see a cost of 32.07. More precisely, 32.072733877455676.

###Finding the optimal parameters using Gradient Descent
def gradientDescent(X, y, theta, alpha, iterations):
for _ in range(iterations):
temp = np.dot(X, theta) - y
temp = np.dot(X.T, temp)
theta = theta - (alpha/m) * temp
return theta
theta = gradientDescent(X, y, theta, alpha, iterations)
print(theta)
#Expected theta values [-3.6303, 1.1664]
#Technically,
#[[-3.63029144]
# [ 1.16636235]]
#
# So, for instance, the first row of actual data goes like this.
# Population (10,000) Profit ($10,000)
# 6.1101 17.592
#
# An estimated profit for this population is
# -3.6303 * 1 + 1.1664 * 6.1101 = 3.49652064

#We now have the optimized value of theta . Use this value in the above cost function.

J = computeCost(X, y, theta)
print(J)
#It should give you a value of 4.483 (4.483388256587726) which is much better than 32.07

### Plot showing the best fit line
plt.scatter(X[:,1], y)
plt.xlabel('Population of City in 10,000s')
plt.ylabel('Profit in $10,000s')
plt.plot(X[:,1], np.dot(X, theta))
plt.savefig('fig_1a.2.png') # Save an image file
plt.show()

1b_liner_regression_w_multiple_variables.py

########## Python Implementation of Andrew Ng’s Machine Learning Course (Part 1)
########## Linear Regression with multiple variables
#(also called Multivariate Linear Regression)

# ex1data2.txt
# a training set of housing prices in Portland, Oregon
# column data
# 1 size of the house (in square feet)
# 2 number of bedrooms
# 3 price of the house

### import
import numpy as np
import pandas as pd

### data loading
data = pd.read_csv('ex1data2.txt', sep = ',', header = None)
X = data.iloc[:,0:2] # read first two columns into X
y = data.iloc[:,2] # read the third column into y
m = len(y) # no. of training samples
data.head()

### Feature Normalization
X = (X - np.mean(X))/np.std(X)

###Adding the intercept term and initializing parameters
ones = np.ones((m,1))
X = np.hstack((ones, X))
alpha = 0.01
num_iters = 400
theta = np.zeros((3,1))
y = y[:,np.newaxis]

###Computing the cost
def computeCostMulti(X, y, theta):
temp = np.dot(X, theta) - y
return np.sum(np.power(temp, 2)) / (2*m)
J = computeCostMulti(X, y, theta)
print(J)
#You should expect to see a cost of 65591548106.45744.

###Finding the optimal parameters using Gradient Descent
def gradientDescentMulti(X, y, theta, alpha, iterations):
m = len(y)
for _ in range(iterations):
temp = np.dot(X, theta) - y
temp = np.dot(X.T, temp)
theta = theta - (alpha/m) * temp
return theta
theta = gradientDescentMulti(X, y, theta, alpha, num_iters)
print(theta)
# your optimal parameters will be [[334302.06399328],[ 99411.44947359], [3267.01285407]]
# For instance, if you look at the sample data in the first row,
# 2104 3 399900
# first column's average: 2000.68085106383
# first column's SD: 794.70235353389
# second column's average: 3.17021276595745
# second column's SD: 0.7609818867801
#
# So, the first column (2104-2000.68085106383)/794.70235353389 = 0.1300 (SD)
# Then the second column (3-3.17021276595745)/0.7609818867801 = -0.2237 (SD)

# 334302.06399328 * 1 + 99411.44947359 * 0.1300 + 3267.01285407 * (-0.2237)
# = 346494.721649391 (estimated data) ~ 399,900 (actual data)

#We now have the optimized value of theta . Use this value in the above cost function.
J = computeCostMulti(X, y, theta)
print(J)
#This should give you a value of 2105448288.6292474 which is much better than 65591548106.45744

2.1_logistic_regression_or_classification.py

########## Python Implementation of Andrew Ng’s Machine Learning Course (Part 2.1)
########## Logistic Regression or Classification (part 2.1)
#
# Reference:
# https://medium.com/analytics-vidhya/python-implementation-of-andrew-ngs-machine-learning-course-part-2-1-1a666f049ad6
#
#

##### Logistic Regression

### import libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt # more on this later

### data
#ex2data1.txt
#column data
#1 Exam 1 score
#2 Exam 2 score
#3 0 (fail) or 1 (pass)

data = pd.read_csv('ex2data1.txt', header = None)
X = data.iloc[:,:-1]
y = data.iloc[:,2]
data.head()

### plotting

mask = y == 1
adm = plt.scatter(X[mask][0].values, X[mask][1].values)
not_adm = plt.scatter(X[~mask][0].values, X[~mask][1].values)
plt.xlabel('Exam 1 score')
plt.ylabel('Exam 2 score')
plt.legend((adm, not_adm), ('Admitted', 'Not admitted'))
plt.savefig('fig_2.1.1.png') # Save an image file
plt.show()

### Implementation

## Sigmoid Function

def sigmoid(x):
return 1/(1+np.exp(-x))

## Cost Function
def costFunction(theta, X, y):
J = (-1/m) * np.sum(np.multiply(y, np.log(sigmoid(X @ theta)))
+ np.multiply((1-y), np.log(1 - sigmoid(X @ theta))))
return J

## Gradient Function
def gradient(theta, X, y):
return ((1/m) * X.T @ (sigmoid(X @ theta) - y))

(m, n) = X.shape
X = np.hstack((np.ones((m,1)), X))
y = y[:, np.newaxis]
theta = np.zeros((n+1,1)) # intializing theta with all zeros
J = costFunction(theta, X, y)
print(J)
# This should give us a value of 0.693 for J.
# More precisely, 0.6931471805599453

### Learning parameters using fmin_tnc
temp = opt.fmin_tnc(func = costFunction,
x0 = theta.flatten(),fprime = gradient,
args = (X, y.flatten()))
#the output of above function is a tuple whose first element #contains the optimized values of theta
theta_optimized = temp[0]
print(theta_optimized)
# The above code should give [-25.16131862, 0.20623159, 0.20147149].

J = costFunction(theta_optimized[:,np.newaxis], X, y)
print(J)
#You should see a value of 0.203 (0.20349770158947486).
# Compare this with the cost 0.693 obtained using initial theta.

### Plotting Decision Boundary (Optional)
plot_x = [np.min(X[:,1]-2), np.max(X[:,2]+2)]
plot_y = -1/theta_optimized[2]*(theta_optimized[0]
+ np.dot(theta_optimized[1],plot_x))
mask = y.flatten() == 1
adm = plt.scatter(X[mask][:,1], X[mask][:,2])
not_adm = plt.scatter(X[~mask][:,1], X[~mask][:,2])
decision_boun = plt.plot(plot_x, plot_y)
plt.xlabel('Exam 1 score')
plt.ylabel('Exam 2 score')
plt.legend((adm, not_adm), ('Admitted', 'Not admitted'))
plt.savefig('fig_2.1.2.png') # Save an image file
plt.show()

def accuracy(X, y, theta, cutoff):
pred = [sigmoid(np.dot(X, theta)) >= cutoff]
acc = np.mean(pred == y)
print(acc * 100)
accuracy(X, y.flatten(), theta_optimized, 0.5)

# This should give us an accuracy score of 89% . Hmm… not bad.

2.2_regularized_logistic_regression.py

########## Python Implementation of Andrew Ng’s Machine Learning Course (Part 2.2)
########## Regularized Logistic Regression (part 2.2)
#
# Reference:
# https://medium.com/analytics-vidhya/python-implementation-of-andrew-ngs-machine-learning-course-part-2-2-dceff1a12a12
#
#

##### Regularized logistic regression

### import libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt # more on this later

### data
#ex2data2.txt
#column data
#1 test 1 result
#2 test 2 result
#3 0 (rejected) or 1 (accepted)

data = pd.read_csv('ex2data2.txt', header = None)
X = data.iloc[:,:-1]
y = data.iloc[:,2]
data.head()

### plotting
mask = y == 1
passed = plt.scatter(X[mask][0].values, X[mask][1].values)
failed = plt.scatter(X[~mask][0].values, X[~mask][1].values)
plt.xlabel('Microchip Test1')
plt.ylabel('Microchip Test2')
plt.legend((passed, failed), ('Passed', 'Failed'))
plt.savefig('fig_2.2.1.png') # Save an image file
plt.show()

### Feature mapping
def mapFeature(X1, X2):
degree = 6
out = np.ones(X.shape[0])[:,np.newaxis]
for i in range(1, degree+1):
for j in range(i+1):
out = np.hstack((out, np.multiply(np.power(X1, i-j), np.power(X2, j))[:,np.newaxis]))
return out
X = mapFeature(X.iloc[:,0], X.iloc[:,1])

### Implementation

## Sigmoid Function
def sigmoid(x):
return 1/(1+np.exp(-x))

## Cost Function
def lrCostFunction(theta_t, X_t, y_t, lambda_t):
m = len(y_t)
J = (-1/m) * (y_t.T @ np.log(sigmoid(X_t @ theta_t)) + (1 - y_t.T) @ np.log(1 - sigmoid(X_t @ theta_t)))
reg = (lambda_t/(2*m)) * (theta_t[1:].T @ theta_t[1:])
J = J + reg
return J

## Gradient Function
def lrGradientDescent(theta, X, y, lambda_t):
m = len(y)
grad = np.zeros([m,1])
grad = (1/m) * X.T @ (sigmoid(X @ theta) - y)
grad[1:] = grad[1:] + (lambda_t / m) * theta[1:]
return grad

(m, n) = X.shape
y = y[:, np.newaxis]
theta = np.zeros((n,1))
lmbda = 1
J = lrCostFunction(theta, X, y, lmbda)
print(J)
#This gives us a values of 0.69314718.

## Learning parameters using fmin_tnc
output = opt.fmin_tnc(func = lrCostFunction, x0 = theta.flatten(), fprime = lrGradientDescent, \
args = (X, y.flatten(), lmbda))
theta = output[0]
print(theta) # theta contains the optimized values

## Accuracy of model
pred = [sigmoid(np.dot(X, theta)) >= 0.5]
np.mean(pred == y.flatten()) * 100
print(np.mean(pred == y.flatten()) * 100)
# This gives our model accuracy as 83.05% (83.05084745762711).

## Plotting Decision Boundary (optional)
u = np.linspace(-1, 1.5, 50)
v = np.linspace(-1, 1.5, 50)
z = np.zeros((len(u), len(v)))
def mapFeatureForPlotting(X1, X2):
degree = 6
out = np.ones(1)
for i in range(1, degree+1):
for j in range(i+1):
out = np.hstack((out, np.multiply(np.power(X1, i-j), np.power(X2, j))))
return out
for i in range(len(u)):
for j in range(len(v)):
z[i,j] = np.dot(mapFeatureForPlotting(u[i], v[j]), theta)
mask = y.flatten() == 1
X = data.iloc[:,:-1]
passed = plt.scatter(X[mask][0], X[mask][1])
failed = plt.scatter(X[~mask][0], X[~mask][1])
plt.contour(u,v,z,0)
plt.xlabel('Microchip Test1')
plt.ylabel('Microchip Test2')
plt.legend((passed, failed), ('Passed', 'Failed'))
plt.savefig('fig_2.2.2.png') # Save an image file
plt.show()

data

ex1data1.txt

6.1101,17.592
5.5277,9.1302
8.5186,13.662
7.0032,11.854
5.8598,6.8233
8.3829,11.886
7.4764,4.3483
8.5781,12
6.4862,6.5987
5.0546,3.8166
5.7107,3.2522
14.164,15.505
5.734,3.1551
8.4084,7.2258
5.6407,0.71618
5.3794,3.5129
6.3654,5.3048
5.1301,0.56077
6.4296,3.6518
7.0708,5.3893
6.1891,3.1386
20.27,21.767
5.4901,4.263
6.3261,5.1875
5.5649,3.0825
18.945,22.638
12.828,13.501
10.957,7.0467
13.176,14.692
22.203,24.147
5.2524,-1.22
6.5894,5.9966
9.2482,12.134
5.8918,1.8495
8.2111,6.5426
7.9334,4.5623
8.0959,4.1164
5.6063,3.3928
12.836,10.117
6.3534,5.4974
5.4069,0.55657
6.8825,3.9115
11.708,5.3854
5.7737,2.4406
7.8247,6.7318
7.0931,1.0463
5.0702,5.1337
5.8014,1.844
11.7,8.0043
5.5416,1.0179
7.5402,6.7504
5.3077,1.8396
7.4239,4.2885
7.6031,4.9981
6.3328,1.4233
6.3589,-1.4211
6.2742,2.4756
5.6397,4.6042
9.3102,3.9624
9.4536,5.4141
8.8254,5.1694
5.1793,-0.74279
21.279,17.929
14.908,12.054
18.959,17.054
7.2182,4.8852
8.2951,5.7442
10.236,7.7754
5.4994,1.0173
20.341,20.992
10.136,6.6799
7.3345,4.0259
6.0062,1.2784
7.2259,3.3411
5.0269,-2.6807
6.5479,0.29678
7.5386,3.8845
5.0365,5.7014
10.274,6.7526
5.1077,2.0576
5.7292,0.47953
5.1884,0.20421
6.3557,0.67861
9.7687,7.5435
6.5159,5.3436
8.5172,4.2415
9.1802,6.7981
6.002,0.92695
5.5204,0.152
5.0594,2.8214
5.7077,1.8451
7.6366,4.2959
5.8707,7.2029
5.3054,1.9869
8.2934,0.14454
13.394,9.0551
5.4369,0.61705

ex1data2.txt

2104,3,399900
1600,3,329900
2400,3,369000
1416,2,232000
3000,4,539900
1985,4,299900
1534,3,314900
1427,3,198999
1380,3,212000
1494,3,242500
1940,4,239999
2000,3,347000
1890,3,329999
4478,5,699900
1268,3,259900
2300,4,449900
1320,2,299900
1236,3,199900
2609,4,499998
3031,4,599000
1767,3,252900
1888,2,255000
1604,3,242900
1962,4,259900
3890,3,573900
1100,3,249900
1458,3,464500
2526,3,469000
2200,3,475000
2637,3,299900
1839,2,349900
1000,1,169900
2040,4,314900
3137,3,579900
1811,4,285900
1437,3,249900
1239,3,229900
2132,4,345000
4215,4,549000
2162,4,287000
1664,2,368500
2238,3,329900
2567,4,314000
1200,3,299000
852,2,179900
1852,4,299900
1203,3,239500

ex2data1.txt

34.62365962451697,78.0246928153624,0
30.28671076822607,43.89499752400101,0
35.84740876993872,72.90219802708364,0
60.18259938620976,86.30855209546826,1
79.0327360507101,75.3443764369103,1
45.08327747668339,56.3163717815305,0
61.10666453684766,96.51142588489624,1
75.02474556738889,46.55401354116538,1
76.09878670226257,87.42056971926803,1
84.43281996120035,43.53339331072109,1
95.86155507093572,38.22527805795094,0
75.01365838958247,30.60326323428011,0
82.30705337399482,76.48196330235604,1
69.36458875970939,97.71869196188608,1
39.53833914367223,76.03681085115882,0
53.9710521485623,89.20735013750205,1
69.07014406283025,52.74046973016765,1
67.94685547711617,46.67857410673128,0
70.66150955499435,92.92713789364831,1
76.97878372747498,47.57596364975532,1
67.37202754570876,42.83843832029179,0
89.67677575072079,65.79936592745237,1
50.534788289883,48.85581152764205,0
34.21206097786789,44.20952859866288,0
77.9240914545704,68.9723599933059,1
62.27101367004632,69.95445795447587,1
80.1901807509566,44.82162893218353,1
93.114388797442,38.80067033713209,0
61.83020602312595,50.25610789244621,0
38.78580379679423,64.99568095539578,0
61.379289447425,72.80788731317097,1
85.40451939411645,57.05198397627122,1
52.10797973193984,63.12762376881715,0
52.04540476831827,69.43286012045222,1
40.23689373545111,71.16774802184875,0
54.63510555424817,52.21388588061123,0
33.91550010906887,98.86943574220611,0
64.17698887494485,80.90806058670817,1
74.78925295941542,41.57341522824434,0
34.1836400264419,75.2377203360134,0
83.90239366249155,56.30804621605327,1
51.54772026906181,46.85629026349976,0
94.44336776917852,65.56892160559052,1
82.36875375713919,40.61825515970618,0
51.04775177128865,45.82270145776001,0
62.22267576120188,52.06099194836679,0
77.19303492601364,70.45820000180959,1
97.77159928000232,86.7278223300282,1
62.07306379667647,96.76882412413983,1
91.56497449807442,88.69629254546599,1
79.94481794066932,74.16311935043758,1
99.2725269292572,60.99903099844988,1
90.54671411399852,43.39060180650027,1
34.52451385320009,60.39634245837173,0
50.2864961189907,49.80453881323059,0
49.58667721632031,59.80895099453265,0
97.64563396007767,68.86157272420604,1
32.57720016809309,95.59854761387875,0
74.24869136721598,69.82457122657193,1
71.79646205863379,78.45356224515052,1
75.3956114656803,85.75993667331619,1
35.28611281526193,47.02051394723416,0
56.25381749711624,39.26147251058019,0
30.05882244669796,49.59297386723685,0
44.66826172480893,66.45008614558913,0
66.56089447242954,41.09209807936973,0
40.45755098375164,97.53518548909936,1
49.07256321908844,51.88321182073966,0
80.27957401466998,92.11606081344084,1
66.74671856944039,60.99139402740988,1
32.72283304060323,43.30717306430063,0
64.0393204150601,78.03168802018232,1
72.34649422579923,96.22759296761404,1
60.45788573918959,73.09499809758037,1
58.84095621726802,75.85844831279042,1
99.82785779692128,72.36925193383885,1
47.26426910848174,88.47586499559782,1
50.45815980285988,75.80985952982456,1
60.45555629271532,42.50840943572217,0
82.22666157785568,42.71987853716458,0
88.9138964166533,69.80378889835472,1
94.83450672430196,45.69430680250754,1
67.31925746917527,66.58935317747915,1
57.23870631569862,59.51428198012956,1
80.36675600171273,90.96014789746954,1
68.46852178591112,85.59430710452014,1
42.0754545384731,78.84478600148043,0
75.47770200533905,90.42453899753964,1
78.63542434898018,96.64742716885644,1
52.34800398794107,60.76950525602592,0
94.09433112516793,77.15910509073893,1
90.44855097096364,87.50879176484702,1
55.48216114069585,35.57070347228866,0
74.49269241843041,84.84513684930135,1
89.84580670720979,45.35828361091658,1
83.48916274498238,48.38028579728175,1
42.2617008099817,87.10385094025457,1
99.31500880510394,68.77540947206617,1
55.34001756003703,64.9319380069486,1
74.77589300092767,89.52981289513276,1

ex2data2.txt

0.051267,0.69956,1
-0.092742,0.68494,1
-0.21371,0.69225,1
-0.375,0.50219,1
-0.51325,0.46564,1
-0.52477,0.2098,1
-0.39804,0.034357,1
-0.30588,-0.19225,1
0.016705,-0.40424,1
0.13191,-0.51389,1
0.38537,-0.56506,1
0.52938,-0.5212,1
0.63882,-0.24342,1
0.73675,-0.18494,1
0.54666,0.48757,1
0.322,0.5826,1
0.16647,0.53874,1
-0.046659,0.81652,1
-0.17339,0.69956,1
-0.47869,0.63377,1
-0.60541,0.59722,1
-0.62846,0.33406,1
-0.59389,0.005117,1
-0.42108,-0.27266,1
-0.11578,-0.39693,1
0.20104,-0.60161,1
0.46601,-0.53582,1
0.67339,-0.53582,1
-0.13882,0.54605,1
-0.29435,0.77997,1
-0.26555,0.96272,1
-0.16187,0.8019,1
-0.17339,0.64839,1
-0.28283,0.47295,1
-0.36348,0.31213,1
-0.30012,0.027047,1
-0.23675,-0.21418,1
-0.06394,-0.18494,1
0.062788,-0.16301,1
0.22984,-0.41155,1
0.2932,-0.2288,1
0.48329,-0.18494,1
0.64459,-0.14108,1
0.46025,0.012427,1
0.6273,0.15863,1
0.57546,0.26827,1
0.72523,0.44371,1
0.22408,0.52412,1
0.44297,0.67032,1
0.322,0.69225,1
0.13767,0.57529,1
-0.0063364,0.39985,1
-0.092742,0.55336,1
-0.20795,0.35599,1
-0.20795,0.17325,1
-0.43836,0.21711,1
-0.21947,-0.016813,1
-0.13882,-0.27266,1
0.18376,0.93348,0
0.22408,0.77997,0
0.29896,0.61915,0
0.50634,0.75804,0
0.61578,0.7288,0
0.60426,0.59722,0
0.76555,0.50219,0
0.92684,0.3633,0
0.82316,0.27558,0
0.96141,0.085526,0
0.93836,0.012427,0
0.86348,-0.082602,0
0.89804,-0.20687,0
0.85196,-0.36769,0
0.82892,-0.5212,0
0.79435,-0.55775,0
0.59274,-0.7405,0
0.51786,-0.5943,0
0.46601,-0.41886,0
0.35081,-0.57968,0
0.28744,-0.76974,0
0.085829,-0.75512,0
0.14919,-0.57968,0
-0.13306,-0.4481,0
-0.40956,-0.41155,0
-0.39228,-0.25804,0
-0.74366,-0.25804,0
-0.69758,0.041667,0
-0.75518,0.2902,0
-0.69758,0.68494,0
-0.4038,0.70687,0
-0.38076,0.91886,0
-0.50749,0.90424,0
-0.54781,0.70687,0
0.10311,0.77997,0
0.057028,0.91886,0
-0.10426,0.99196,0
-0.081221,1.1089,0
0.28744,1.087,0
0.39689,0.82383,0
0.63882,0.88962,0
0.82316,0.66301,0
0.67339,0.64108,0
1.0709,0.10015,0
-0.046659,-0.57968,0
-0.23675,-0.63816,0
-0.15035,-0.36769,0
-0.49021,-0.3019,0
-0.46717,-0.13377,0
-0.28859,-0.060673,0
-0.61118,-0.067982,0
-0.66302,-0.21418,0
-0.59965,-0.41886,0
-0.72638,-0.082602,0
-0.83007,0.31213,0
-0.72062,0.53874,0
-0.59389,0.49488,0
-0.48445,0.99927,0
-0.0063364,0.99927,0
0.63265,-0.030612,0

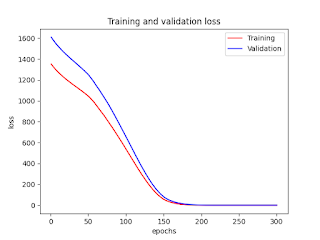
After running r scripts above, you'll get these png files on your working directory on your Terminal: