The Financial Journal (Global): Package: Data Generation, Data Loading and Standardization, Initial Data Analysis, Multiple Linear Regression, Polynominal Liner Regression in Python

Package: Data Generation, Data Loading and Standardization, Initial Data Analysis, Multiple Linear Regression, Polynominal Liner Regression in Python

**0_MacOS_Python_setup.txt**
# Install on Terminal of MacOS # 1. pandas #pip3 install -U pandas # 2. NumPy #pip3 install -U numpy # 3. matplotlib #pip3 install -U matplotlib # 4. scikit-learn (sklearn) #pip3 install -U scikit-learn # 5. statsmodels #pip3 install -U statsmodels

1_MacOS_Terminal.txt

########## Run Terminal on MacOS and execute
### TO UPDATE
cd "YOUR_WORKING_DIRECTORY"

python3 stpkg00.py

#python3 stpkg01.py
python3 stpkg01.py yX.csv y

python3 stpkg02.py yXSTD.csv

#Multiple Linear Regression
python3 stpkg03.py yXSTD.csv y x1 x2 x3

#Polynomial SINGLE Linear Regression
python3 stpkg04.py yXSTD.csv y x1 3

Input data files

N/A

NaN

Python files

stpkg00.py

#################### Data Generation ####################

'''

x1raw = σ(1,1)
x2raw = σ(2,2)
x3raw = x1 + σ(2,2)

x1 = σ(0,1)
x2 = σ(0,1)
x3 = σ(0,1)

y = 1.0 + (2.0 * x1) + (0.5 * x2) + (0.1 * x3) + (0.05 * x1 * x2) + (0.2 * (x1)^2) + (0.02 * (x1)^3) + σ(0,1)
'''

import scipy as sp
import pandas as pd
from sklearn.preprocessing import StandardScaler
#import math
import numpy as np

sp.random.seed(0)

#numbe of samples
n = 100

x1 = sp.random.normal(1,1,n)
x2 = sp.random.normal(2,2,n)
x3 = x1 + sp.random.normal(2,2,n)
#
#print(x1)
#[ 2.76405235 ...
#print(type(x1))
#<class 'numpy.ndarray'>
#
#print(x2)
#[ 5.76630139e+00 ...
#
#print(x3)
#[ 4.02568867 ...

x1 = pd.DataFrame(x1)
x1 = x1.rename(columns={0: 'x1'})
#print(x1)

x2 = pd.DataFrame(x2)
x2 = x2.rename(columns={0: 'x2'})
#print(x2)

x3 = pd.DataFrame(x3)
x3 = x3.rename(columns={0: 'x3'})
#print(x3)

X = pd.concat([x1, x2, x3], axis=1)
#print(X)
#print(X.describe()) #standard deviation (sample, NOT population)

X.to_csv('X.csv', header=True, index=False)

#scaler = StandardScaler()
scaler = StandardScaler()
scaler.fit(X)

#print(scaler.mean_) # mean
#[1.05980802 2.16402594 2.94134349]
#
#print(scaler.var_) # variance
#print(type(scaler.var_))
#<class 'numpy.ndarray'>
#print((scaler.var_) ** 0.5) # standard deviation　(population)
#[1.00788224 2.06933399 2.22108027]

XSTD = pd.DataFrame(scaler.transform(X))
XSTD = XSTD.rename(columns={0: 'x1', 1: 'x2', 2: 'x3'})
XSTD.to_csv('XSTD.csv', header=True, index=False)
#print(XSTD)
'''
x1 x2 x3
0 1.690916 1.740790 0.488206
1 0.337687 -1.381867 -0.008980
2 0.911743 -1.307182 1.457270
3 2.164028 0.857652 1.625370
4 1.793612 -1.213082 1.443657
.. ... ... ...
95 0.641707 -0.245064 1.368259
96 -0.048922 0.666666 0.119134
97 1.712564 0.716647 1.355392
98 0.066579 2.011491 -0.276140
99 0.339505 1.212482 0.540619

[100 rows x 3 columns]
#
print(XSTD.describe())
'''
'''
x1 x2 x3
count 1.000000e+02 1.000000e+02 1.000000e+02
mean -1.143530e-16 1.576517e-16 -5.440093e-17
std 1.005038e+00 1.005038e+00 1.005038e+00
min -2.592364e+00 -2.228172e+00 -2.412135e+00
25% -6.981616e-01 -7.997189e-01 -6.266296e-01
50% 3.401995e-02 -5.543630e-02 1.232380e-02
75% 6.719727e-01 7.398196e-01 6.364589e-01
max 2.192663e+00 2.224031e+00 2.300629e+00
'''

#print(XSTD['x1'])
#print(type(XSTD['x1']))
#<class 'pandas.core.series.Series'>
#
#print(np.array(XSTD['x1']))
#print(type(np.array(XSTD['x1'])))
#<class 'numpy.ndarray'>

tmpy = (2.0 * np.array(XSTD['x1']))
tmpy = tmpy + (0.5 * np.array(XSTD['x2']))
tmpy = tmpy + (0.1 * np.array(XSTD['x3']))
tmpy = tmpy + (0.05 * np.array(XSTD['x1']) * np.array(XSTD['x2']))
tmpy = tmpy + (0.2 * (np.array(XSTD['x1']) ** 2))
tmpy = tmpy + (0.02 * (np.array(XSTD['x1']) ** 3))
tmpy = tmpy + sp.random.normal(0,1,n)
tmpy = tmpy + 1.0
#print(tmpy)
#print(type(tmpy))
#<class 'numpy.ndarray'>
y = pd.DataFrame(tmpy)
y = y.rename(columns={0: 'y'})
y.to_csv('y.csv', header=True, index=False)

#print(y)
#print(type(y))
#<class 'pandas.core.frame.DataFrame'>

#y = 1.0 + (2.0 * x1) + (0.5 * x2) + (0.1 * x3) + (0.05 * x1 * x2) + (0.2 * (x1)^2) + (0.02 * (x1)^3) + σ(0,1)
#y = 1.0 + (2.0 * x1) + (0.5 * x2) + (0.1 * x3) + (0.05 * x1 * x2) + (0.2 * (x1**2)) + (0.02 * (x1**3)) + sp.random.normal(0,1,n)
#y = 1.0 + (2.0 * 1.690916) + (0.5 * 1.740790) + (0.1 * 0.488206) + (0.05 * 1.690916 * 1.740790) + (0.2 * (1.690916**2)) + (0.02 * (1.690916**3)) + 0
#print(1.0 + (2.0 * 1.690916) + (0.5 * 1.740790) + (0.1 * 0.488206) + (0.05 * 1.690916 * 1.740790) + (0.2 * (1.690916**2)) + (0.02 * (1.690916**3)) + 0)
#6.11675670334485

yX = pd.concat([y, x1, x2, x3], axis=1)
yX.to_csv('yX.csv', header=True, index=False)

stpkg01.py

#################### Data Loading and Standardization

########## data file(s) to load
# yX.csv (which includes dependent variable y and indepdent variables X: x1, x2, ...)
##########

########## Run this code as follows
#python3 stpkg01.py yX.csv y
#python3 stpkg01.py (data file to load) (dependent variable/target in yX.csv)

########## import
import sys
import pandas as pd
from sklearn.preprocessing import StandardScaler

#print(sys.argv[0])
#stpkg01.py
#
dfname = sys.argv[1]
yname = sys.argv[2]
##########

########## loading data
#yX = pd.read_csv('yX.csv', header = 0)
yX = pd.read_csv(dfname, header = 0)
#
print(yX)
#print(yX.describe())

#X = yX.drop(['y'], axis=1)
X = yX.drop([yname], axis=1)
#print(X)
X.to_csv('X.csv', header=True, index=False)

#y = yX['y']
y = yX[yname]
y.to_csv('y.csv', header=True, index=False)

scaler = StandardScaler()
scaler.fit(X)

#print(scaler.mean_) # mean
#[1.05980802 2.16402594 2.94134349]
#
#print((scaler.var_) ** 0.5) # standard deviation　(population)
#[1.00788224 2.06933399 2.22108027]

XSTD = pd.DataFrame(scaler.transform(X), columns = X.columns)
print(XSTD.describe())
'''
x1 x2 x3
count 1.000000e+02 1.000000e+02 1.000000e+02
mean -1.187939e-16 1.620926e-16 -2.320366e-16
std 1.005038e+00 1.005038e+00 1.005038e+00
min -2.592364e+00 -2.228172e+00 -2.412135e+00
25% -6.981616e-01 -7.997189e-01 -6.266296e-01
50% 3.401995e-02 -5.543630e-02 1.232380e-02
75% 6.719727e-01 7.398196e-01 6.364589e-01
max 2.192663e+00 2.224031e+00 2.300629e+00
'''
XSTD.to_csv('XSTD.csv', header=True, index=False)

yXSTD = pd.concat([y, XSTD], axis=1)
yXSTD.to_csv('yXSTD.csv', header=True, index=False)

stpkg02.py

#################### Initial Data Analysis

########## Run this code as follows
#python3 stpkg02.py yXSTD.csv
#python3 stpkg02.py (data file to load)

########## import
import sys
import pandas as pd
from pandas.plotting import scatter_matrix
import matplotlib.pyplot as plt
import seaborn as sns

#print(sys.argv[0])
#stpkg02.py
#
dfname = sys.argv[1]
##########

########## loading data
#yXSTD = pd.read_csv('yXSTD.csv', header = 0)
yXSTD = pd.read_csv(dfname, header = 0)

#print(yXSTD.describe())
'''
y x1 x2 x3
count 100.000000 1.000000e+02 1.000000e+02 1.000000e+02
mean 1.008893 -1.232348e-16 1.576517e-16 -2.364775e-16
std 2.384226 1.005038e+00 1.005038e+00 1.005038e+00
min -4.001685 -2.592364e+00 -2.228172e+00 -2.412135e+00
25% -0.432215 -6.981616e-01 -7.997189e-01 -6.266296e-01
50% 0.755357 3.401995e-02 -5.543630e-02 1.232380e-02
75% 2.321260 6.719727e-01 7.398196e-01 6.364589e-01
max 6.808487 2.192663e+00 2.224031e+00 2.300629e+00
'''

########## scatter matrix

#scatter_matrix(yXSTD, figsize=(6.4, 4.8)) #640 x 480
scatter_matrix(yXSTD, figsize=(800/100, 600/100))
plt.suptitle('Scatter Matrix')
plt.savefig("Fig_02_1.png")
plt.show()
plt.close()

########## correlation

cor = yXSTD.corr()

#print(cor)

ax = sns.heatmap(
cor,
annot=True,
fmt='.4f', #f for fixed number of decimal places (4 in this case); g is for variable numbers
vmin=-1, vmax=1, center=0,
#cmap='Blues',
cmap=sns.diverging_palette(20, 220, n=200),
square=True
)
ax.set_xticklabels(
ax.get_xticklabels(),
#rotation=45,
horizontalalignment='right'
);

plt.suptitle('Correlation Heatmap')
plt.savefig("Fig_02_2.png")
plt.show()
plt.close()

stpkg03.py

#################### Multiple Linear Regression

########## Run this code as follows
#python3 stpkg03.py yXSTD.csv y x1 x2 x3
#python3 stpkg03.py (data file to load) (dependent variable/target in yXSTD.csv) (3 specified independent variables in yXSTD.csv for multiple linear regression)

########## import
import sys
import pandas as pd
from sklearn.model_selection import train_test_split
#from sklearn.linear_model import LinearRegression
from sklearn import linear_model
import statsmodels.api as sm
import matplotlib.pyplot as plt
#from pandas.plotting import scatter_matrix
#import seaborn as sns

#print(sys.argv[0])
#stpkg03.py
#
dfname = sys.argv[1]
yname = sys.argv[2]
x1name = sys.argv[3]
x2name = sys.argv[4]
x3name = sys.argv[5]
##########

########## loading data
#yXSTD = pd.read_csv('yXSTD.csv', header = 0)
yXSTD = pd.read_csv(dfname, header = 0)

#print(yXSTD.describe())
'''
y x1 x2 x3
count 100.000000 1.000000e+02 1.000000e+02 1.000000e+02
mean 1.008893 -1.232348e-16 1.576517e-16 -2.364775e-16
std 2.384226 1.005038e+00 1.005038e+00 1.005038e+00
min -4.001685 -2.592364e+00 -2.228172e+00 -2.412135e+00
25% -0.432215 -6.981616e-01 -7.997189e-01 -6.266296e-01
50% 0.755357 3.401995e-02 -5.543630e-02 1.232380e-02
75% 2.321260 6.719727e-01 7.398196e-01 6.364589e-01
max 6.808487 2.192663e+00 2.224031e+00 2.300629e+00
'''

XSTD = yXSTD.drop([yname], axis=1)
#print(XSTD)
#print(type(XSTD))
#X.to_csv('XSTD.csv', header=True, index=False)

y = yXSTD[yname]
y = pd.DataFrame(y)
#print(y)
#print(type(y))
#y.to_csv('y.csv', header=True, index=False)
##########

########## creating training and test data

XSTD_train, XSTD_test, y_train, y_test = train_test_split(XSTD, y, test_size=0.2, random_state = 0)

#print(XSTD_train.shape)
#print(XSTD_test.shape)
#print(y_train.shape)
#print(y_test.shape)
'''
(80, 3)
(20, 3)
(80, 1)
(20, 1)
'''
lr = linear_model.LinearRegression().fit(XSTD_train, y_train)
print(f"R2 of Training Data: {lr.score(XSTD_train, y_train):.4}")
print(f"R2 of Test Data (based on a model by Training Data): {lr.score(XSTD_test, y_test):.4}")

########## Multiple Linear Regression (with Training Data)

smXSTD_train = sm.add_constant(XSTD_train)

model = sm.OLS(y_train, smXSTD_train)

results = model.fit()

print(results.summary())
'''
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.839
Model: OLS Adj. R-squared: 0.832
Method: Least Squares F-statistic: 131.5
Date: Sun, 12 Jul 2020 Prob (F-statistic): 5.23e-30
Time: 18:49:50 Log-Likelihood: -111.79
No. Observations: 80 AIC: 231.6
Df Residuals: 76 BIC: 241.1
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 1.0679 0.113 9.487 0.000 0.844 1.292
x1 1.8865 0.137 13.767 0.000 1.614 2.159
x2 0.5003 0.111 4.490 0.000 0.278 0.722
x3 0.3011 0.135 2.230 0.029 0.032 0.570
==============================================================================
Omnibus: 0.606 Durbin-Watson: 2.329
Prob(Omnibus): 0.739 Jarque-Bera (JB): 0.733
Skew: -0.178 Prob(JB): 0.693
Kurtosis: 2.694 Cond. No. 1.96
==============================================================================

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
'''
with open('results.summary.txt', 'w') as f:
print(results.summary(), file=f)

#print(results.params)
#print(type(results.params))
#<class 'pandas.core.series.Series'>
#
#print(results.params.shape)
#(4,)
#
#print(len(results.params))
#4

b0 = results.params['const']
b1 = results.params[x1name]
b2 = results.params[x2name]
b3 = results.params[x3name]

#print(b0) #1.0679105398301059
#print(b1) #1.8865026849796247
#print(b2) #0.5003158682861151
#print(b3) #0.3010874982341183

#print('R2: ', results.rsquared)
#R2: 0.8385140722177117

#################### traing data integration

#print(pd.concat([y_train, XSTD_train], axis=1))
yXypred_train = pd.concat([y_train, XSTD_train, b0 + (b1 * XSTD_train[x1name]) + (b2 * XSTD_train[x2name]) + (b3 * XSTD_train[x3name])], axis=1)
yXypred_train = yXypred_train.rename(columns={0: 'ypred'})

yXypred_train = pd.concat([yXypred_train, yXypred_train[yname] - yXypred_train['ypred']], axis=1)
yXypred_train = yXypred_train.rename(columns={0: 'residual'})

yXypred_train.to_csv('yXypred_train.csv', header=True, index=False)

#print(yXypred_train.columns)
#Index(['y', 'x1', 'x2', 'x3', 'ypred'], dtype='object')

########## plot: training data (x1, y) and predicted data (x1, ypred)

#print(max(yXypred_train[x1name]))
#2.164027787075764
#
#print(min(yXypred_train[x1name]))
#-4.001684888412238
#
#print(max(yXypred_train[yname]))
#6.808486625095364
#
#print(min(yXypred_train[yname]))
#-2.5923641824877004

plt.figure(figsize=(8, 8))
#
plt.scatter(yXypred_train[x1name], yXypred_train[yname], color = 'blue', label='Training Data')
#
plt.scatter(yXypred_train[x1name], yXypred_train['ypred'], color = 'red', label='Predicted Data')
#
plt.legend(bbox_to_anchor=(1, 0), loc='lower right', borderaxespad=1, fontsize=10)
plt.title(x1name + ": Training Data, " + yname + ": Training Data and Predicted Data")
plt.xlabel(x1name)
plt.ylabel(yname)
plt.grid(True)
#
plt.text(min(yXypred_train[x1name]), max(yXypred_train[yname]) * 1.00, "y = b0 + (b1 * x1) + (b2 * x2) + (b3 * x3)", size = 10, color = "black")
plt.text(min(yXypred_train[x1name]), max(yXypred_train[yname]) * 0.90, "b0 = " + str(b0), size = 10, color = "black")
plt.text(min(yXypred_train[x1name]), max(yXypred_train[yname]) * 0.80, "b1 = " + str(b1), size = 10, color = "black")
plt.text(min(yXypred_train[x1name]), max(yXypred_train[yname]) * 0.70, "b2 = " + str(b2), size = 10, color = "black")
plt.text(min(yXypred_train[x1name]), max(yXypred_train[yname]) * 0.60, "b3 = " + str(b3), size = 10, color = "black")
plt.text(min(yXypred_train[x1name]), max(yXypred_train[yname]) * 0.50, "R2 = " + str(results.rsquared), size = 10, color = "black")
#
plt.savefig('Fig_03_1a.png')
plt.show()

########## plot: training data (x1) and residual data (y - ypred)

plt.figure(figsize=(8, 8))
#
plt.scatter(yXypred_train[x1name], yXypred_train['residual'], color = 'green', label='Residual (actual - predicted)')
#
plt.legend(bbox_to_anchor=(1, 0), loc='lower right', borderaxespad=1, fontsize=10)
plt.title(x1name + ": Training Data, " + 'residual' + ": Residual (actual - predicted)")
plt.xlabel(x1name)
plt.ylabel('Residual')
plt.grid(True)
#
plt.savefig('Fig_03_1b.png')
plt.show()

#################### test data integration

yXypred_test = pd.concat([y_test, XSTD_test, b0 + (b1 * XSTD_test[x1name]) + (b2 * XSTD_test[x2name]) + (b3 * XSTD_test[x3name])], axis=1)
yXypred_test = yXypred_test.rename(columns={0: 'ypred'})

yXypred_test = pd.concat([yXypred_test, yXypred_test[yname] - yXypred_test['ypred']], axis=1)
yXypred_test = yXypred_test.rename(columns={0: 'residual'})

yXypred_test.to_csv('yXypred_test.csv', header=True, index=False)

#print(yXypred_test.columns)
#Index(['y', 'x1', 'x2', 'x3', 'ypred'], dtype='object')

########## plot: test data (x1, y) and predicted data (x1, ypred)

plt.figure(figsize=(8, 8))
#
plt.scatter(yXypred_test[x1name], yXypred_test[yname], color = 'blue', label='Test Data')
#
plt.scatter(yXypred_test[x1name], yXypred_test['ypred'], color = 'red', label='Predicted Data')
#
plt.legend(bbox_to_anchor=(1, 0), loc='lower right', borderaxespad=1, fontsize=10)
plt.title(x1name + ": Test Data, " + yname + ": Test Data and Predicted Data (based on Training Data)")
plt.xlabel(x1name)
plt.ylabel(yname)
plt.grid(True)
#
plt.text(min(yXypred_test[x1name]), max(yXypred_test[yname]) * 1.00, "y = b0 + (b1 * x1) + (b2 * x2) + (b3 * x3)", size = 10, color = "black")
plt.text(min(yXypred_test[x1name]), max(yXypred_test[yname]) * 0.90, "b0 = " + str(b0), size = 10, color = "black")
plt.text(min(yXypred_test[x1name]), max(yXypred_test[yname]) * 0.80, "b1 = " + str(b1), size = 10, color = "black")
plt.text(min(yXypred_test[x1name]), max(yXypred_test[yname]) * 0.70, "b2 = " + str(b2), size = 10, color = "black")
plt.text(min(yXypred_test[x1name]), max(yXypred_test[yname]) * 0.60, "b3 = " + str(b3), size = 10, color = "black")
#
plt.savefig('Fig_03_2a.png')
plt.show()

########## plot: test data (x1) and residual data (y - ypred)

plt.figure(figsize=(8, 8))
#
plt.scatter(yXypred_test[x1name], yXypred_test['residual'], color = 'green', label='Residual (actual - predicted)')
#
plt.legend(bbox_to_anchor=(1, 0), loc='lower right', borderaxespad=1, fontsize=10)
plt.title(x1name + ": Training Data, " + 'residual' + ": Residual (actual - predicted)")
plt.xlabel(x1name)
plt.ylabel('Residual')
plt.grid(True)
#
plt.savefig('Fig_03_2b.png')
plt.show()

stpkg04.py

#################### Multiple Linear Regression

########## Run this code as follows
#python3 stpkg04.py yXSTD.csv y x1 3
#python3 stpkg04.py (data file to load) (dependent variable/target in yXSTD.csv) (one specified independent variables in yXSTD.csv for polynominal linear regression)

########## import
import sys
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import r2_score
import matplotlib.pyplot as plt

#print(sys.argv[0])
#stpkg04.py
#
dfname = sys.argv[1]
yname = sys.argv[2]
x1name = sys.argv[3]
x1dim = int(sys.argv[4])
#x2name = sys.argv[4]
#x3name = sys.argv[5]
##########

########## loading data
#yXSTD = pd.read_csv('yXSTD.csv', header = 0)
yXSTD = pd.read_csv(dfname, header = 0)

#print(yXSTD.describe())
'''
y x1 x2 x3
count 100.000000 1.000000e+02 1.000000e+02 1.000000e+02
mean 1.008893 -1.232348e-16 1.576517e-16 -2.364775e-16
std 2.384226 1.005038e+00 1.005038e+00 1.005038e+00
min -4.001685 -2.592364e+00 -2.228172e+00 -2.412135e+00
25% -0.432215 -6.981616e-01 -7.997189e-01 -6.266296e-01
50% 0.755357 3.401995e-02 -5.543630e-02 1.232380e-02
75% 2.321260 6.719727e-01 7.398196e-01 6.364589e-01
max 6.808487 2.192663e+00 2.224031e+00 2.300629e+00
'''

XSTD = yXSTD.drop([yname], axis=1)
#print(XSTD)
#print(type(XSTD))
#X.to_csv('XSTD.csv', header=True, index=False)

x1 = XSTD[x1name]
x1 = pd.DataFrame(x1)
#print(x1)
#print(type(x1))
#<class 'pandas.core.frame.DataFrame'>

y = yXSTD[yname]
y = pd.DataFrame(y)
#print(y)
#print(type(y))
#y.to_csv('y.csv', header=True, index=False)
##########

########## creating training and test data

x1_train, x1_test, y_train, y_test = train_test_split(x1, y, test_size=0.2, random_state = 0)

#print(XSTD_train.shape)
#print(XSTD_test.shape)
#print(y_train.shape)
#print(y_test.shape)
'''
(80, 3)
(20, 3)
(80, 1)
(20, 1)
'''
#lr = linear_model.LinearRegression().fit(XSTD_train, y_train)
#print(f"R2 of Training Data: {lr.score(XSTD_train, y_train):.4}")
#print(f"R2 of Test Data (based on a model by Training Data): {lr.score(XSTD_test, y_test):.4}")

########## Polynominal Linear Regression (for Training Data)
clf = LinearRegression()

clf.fit(x1_train, y_train)

#dimension
#print(x1dim)

pf = PolynomialFeatures(degree = x1dim, include_bias = False)
x_poly = pf.fit_transform(x1_train)

poly_reg = LinearRegression()
poly_reg_fit = poly_reg.fit(x_poly, y_train)

#print(poly_reg_fit.coef_)
#[[2.05425368 0.11273714 0.03563863]]
#print(type(poly_reg_fit.coef_))
#<class 'numpy.ndarray'>
#print(poly_reg_fit.coef_[0][0])
#2.0542536782376684
#
#print(poly_reg_fit.intercept_)
#[0.99017672]

polypred = poly_reg.predict(x_poly)

#predicted y
#ypred = clf.predict(y_train)
#ypred = clf.predict(x1_train)
#print(ypred)
#print(type(ypred))
#<class 'numpy.ndarray'>

##### output data

ypred_train = poly_reg_fit.intercept_[0] + (poly_reg_fit.coef_[0][0] * x1_train) + (poly_reg_fit.coef_[0][1] * (x1_train ** 2)) + (poly_reg_fit.coef_[0][2] * (x1_train **3))
ypred_train = ypred_train.rename(columns={x1name: 'ypred'})
#print(ypred_test)

yx1ypred_train = pd.concat([y_train, x1_train, ypred_train], axis=1)
yx1ypred_train.to_csv('yx1ypred_train.csv', header=True, index=False)

yx1ypredres_train = pd.concat([yx1ypred_train, yx1ypred_train[yname] - yx1ypred_train['ypred']], axis=1)
yx1ypredres_train = yx1ypredres_train.rename(columns={0: 'residual'})
yx1ypredres_train.to_csv('yx1ypredres_train.csv', header=True, index=False)

##### plot

plt.scatter(yx1ypredres_train[x1name], yx1ypredres_train[yname], c = 'blue', label = 'Training Data')
plt.scatter(yx1ypredres_train[x1name], yx1ypredres_train['ypred'], c = 'red', label = 'Predicted Data')
#
plt.text(min(yx1ypredres_train[x1name]), max(yx1ypredres_train[yname]) * 1.00, "y = b0 + (b1 * x1) + (b2 * x1^2) + (b3 * x1^3)", size = 10, color = "black")
plt.text(min(yx1ypredres_train[x1name]), max(yx1ypredres_train[yname]) * 0.90, "b0 = " + str(poly_reg_fit.intercept_[0]), size = 10, color = "black")
plt.text(min(yx1ypredres_train[x1name]), max(yx1ypredres_train[yname]) * 0.80, "b1 = " + str(poly_reg_fit.coef_[0][0]), size = 10, color = "black")
plt.text(min(yx1ypredres_train[x1name]), max(yx1ypredres_train[yname]) * 0.70, "b2 = " + str(poly_reg_fit.coef_[0][1]), size = 10, color = "black")
plt.text(min(yx1ypredres_train[x1name]), max(yx1ypredres_train[yname]) * 0.60, "b3 = " + str(poly_reg_fit.coef_[0][2]), size = 10, color = "black")
plt.text(min(yx1ypredres_train[x1name]), max(yx1ypredres_train[yname]) * 0.50, "R^2={}".format(r2_score(y_train, polypred)), size = 10, color = "black")
#
plt.xlabel(x1name + ': Training Data')
plt.ylabel(yname)
plt.grid(True)
#
#plt.legend()
plt.legend(bbox_to_anchor=(1, 0), loc='lower right', borderaxespad=1, fontsize=10)
plt.title("Polynominal Regression: " + x1name)
plt.savefig('Fig_04_1a.png')
plt.show()

'''
#plt.scatter(x1_train, y_train, c = 'blue', label = "R^2={}".format(r2_score(y_train, polypred)))
plt.scatter(x1_train, y_train, c = 'blue', label = 'Training Data')
plt.scatter(x1_train, polypred, c = 'red', label = 'Predicted Data')
#plt.plot(x1_train, polypred, c = 'red')
#
plt.text(min(x1_train[x1name]), max(y_train[yname]) * 1.00, "y = b0 + (b1 * x1) + (b2 * x1^2) + (b3 * x1^3)", size = 10, color = "black")
plt.text(min(x1_train[x1name]), max(y_train[yname]) * 0.90, "b0 = " + str(poly_reg_fit.intercept_[0]), size = 10, color = "black")
plt.text(min(x1_train[x1name]), max(y_train[yname]) * 0.80, "b1 = " + str(poly_reg_fit.coef_[0][0]), size = 10, color = "black")
plt.text(min(x1_train[x1name]), max(y_train[yname]) * 0.70, "b2 = " + str(poly_reg_fit.coef_[0][1]), size = 10, color = "black")
plt.text(min(x1_train[x1name]), max(y_train[yname]) * 0.60, "b3 = " + str(poly_reg_fit.coef_[0][2]), size = 10, color = "black")
plt.text(min(x1_train[x1name]), max(y_train[yname]) * 0.50, "R^2={}".format(r2_score(y_train, polypred)), size = 10, color = "black")
#
plt.xlabel(x1name + ': Training Data')
plt.ylabel(yname)
plt.grid(True)
#
#plt.legend()
plt.legend(bbox_to_anchor=(1, 0), loc='lower right', borderaxespad=1, fontsize=10)
plt.title("Polynominal Regression: " + x1name)
plt.savefig('Fig_04_1a.png')
plt.show()
'''

##### residual plot

plt.scatter(yx1ypredres_train[x1name], yx1ypredres_train['residual'], c = 'green', label = 'Redisual: Training Data')
#
plt.xlabel(x1name + ': Training Data')
plt.ylabel(yname)
plt.grid(True)
#
#plt.legend()
plt.legend(bbox_to_anchor=(1, 0), loc='lower right', borderaxespad=1, fontsize=10)
plt.title("Polynominal Regression, Residual: " + x1name)
plt.savefig('Fig_04_1b.png')
plt.show()

'''
ypred = pd.DataFrame(ypred)
#print(ypred)
#print(type(ypred))
#<class 'pandas.core.frame.DataFrame'>
ypred = ypred.rename(columns={0: 'ypred'})
#
#print(ypred)
#
#print(y_train)
#print(type(y_train))
#
#print(x1_train)
#print(type(x1_train))

y_train.reset_index(drop=True, inplace=True)
y_train = y_train.rename(columns={0: 'y'})
#print(y_train)

x1_train.reset_index(drop=True, inplace=True)
x1_train = x1_train.rename(columns={0: 'x1'})
#print(x1_train)

#yx1ypred_train = pd.concat([y_train, x1_train, ypred], axis=1, ignore_index = True)
yx1ypred_train = pd.concat([y_train, x1_train, ypred], axis=1)
yx1ypred_train.to_csv('yx1ypred_train.csv', header=True, index=False)

yx1ypredres_train = pd.concat([yx1ypred_train, yx1ypred_train[yname] - yx1ypred_train['ypred']], axis=1)
yx1ypredres_train = yx1ypredres_train.rename(columns={0: 'residual'})
yx1ypredres_train.to_csv('yx1ypredres_train.csv', header=True, index=False)

plt.scatter(yx1ypredres_train[x1name], yx1ypredres_train['residual'], c = 'green', label = 'Redisual: Training Data')
#plt.scatter(x1_train, polypred, c = 'red', label = 'Predicted Data')
#plt.plot(x1_train, polypred, c = 'red')
#
#plt.text(min(x1_train[x1name]), max(y_train[yname]) * 1.00, "y = b0 + (b1 * x1) + (b2 * x1^2) + (b3 * x1^3)", size = 10, color = "black")
#plt.text(min(x1_train[x1name]), max(y_train[yname]) * 0.90, "b0 = " + str(poly_reg_fit.intercept_[0]), size = 10, color = "black")
#plt.text(min(x1_train[x1name]), max(y_train[yname]) * 0.80, "b1 = " + str(poly_reg_fit.coef_[0][0]), size = 10, color = "black")
#plt.text(min(x1_train[x1name]), max(y_train[yname]) * 0.70, "b2 = " + str(poly_reg_fit.coef_[0][1]), size = 10, color = "black")
#plt.text(min(x1_train[x1name]), max(y_train[yname]) * 0.60, "b3 = " + str(poly_reg_fit.coef_[0][2]), size = 10, color = "black")
#plt.text(min(x1_train[x1name]), max(y_train[yname]) * 0.50, "R^2={}".format(r2_score(y_train, polypred)), size = 10, color = "black")
#
plt.xlabel(x1name + ': Training Data')
plt.ylabel(yname)
plt.grid(True)
#
#plt.legend()
plt.legend(bbox_to_anchor=(1, 0), loc='lower right', borderaxespad=1, fontsize=10)
plt.title("Polynominal Regression, Residual: " + x1name)
plt.savefig('Fig_04_1b.png')
plt.show()
'''

########## Polynominal Linear Regression (for Test Data)

##### output data

#x1_test
#y_test

ypred_test = poly_reg_fit.intercept_[0] + (poly_reg_fit.coef_[0][0] * x1_test) + (poly_reg_fit.coef_[0][1] * (x1_test ** 2)) + (poly_reg_fit.coef_[0][2] * (x1_test **3))
ypred_test = ypred_test.rename(columns={x1name: 'ypred'})
#print(ypred_test)

yx1ypred_test = pd.concat([y_test, x1_test, ypred_test], axis=1)
yx1ypred_test.to_csv('yx1ypred_test.csv', header=True, index=False)

yx1ypredres_test = pd.concat([yx1ypred_test, yx1ypred_test[yname] - yx1ypred_test['ypred']], axis=1)
yx1ypredres_test = yx1ypredres_test.rename(columns={0: 'residual'})
yx1ypredres_test.to_csv('yx1ypredres_test.csv', header=True, index=False)

##### plot

plt.scatter(yx1ypredres_test[x1name], yx1ypredres_test[yname], c = 'blue', label = 'Test Data')
plt.scatter(yx1ypredres_test[x1name], yx1ypredres_test['ypred'], c = 'red', label = 'Predicted Data')
#
plt.text(min(yx1ypredres_test[x1name]), max(yx1ypredres_test[yname]) * 1.00, "y = b0 + (b1 * x1) + (b2 * x1^2) + (b3 * x1^3)", size = 10, color = "black")
plt.text(min(yx1ypredres_test[x1name]), max(yx1ypredres_test[yname]) * 0.90, "b0 = " + str(poly_reg_fit.intercept_[0]), size = 10, color = "black")
plt.text(min(yx1ypredres_test[x1name]), max(yx1ypredres_test[yname]) * 0.80, "b1 = " + str(poly_reg_fit.coef_[0][0]), size = 10, color = "black")
plt.text(min(yx1ypredres_test[x1name]), max(yx1ypredres_test[yname]) * 0.70, "b2 = " + str(poly_reg_fit.coef_[0][1]), size = 10, color = "black")
plt.text(min(yx1ypredres_test[x1name]), max(yx1ypredres_test[yname]) * 0.60, "b3 = " + str(poly_reg_fit.coef_[0][2]), size = 10, color = "black")
#plt.text(min(yx1ypredres_test[x1name]), max(yx1ypredres_test[yname]) * 0.50, "R^2={}".format(r2_score(y_train, polypred)), size = 10, color = "black")
#
plt.xlabel(x1name + ': Test Data')
plt.ylabel(yname)
plt.grid(True)
#
#plt.legend()
plt.legend(bbox_to_anchor=(1, 0), loc='lower right', borderaxespad=1, fontsize=10)
plt.title("Polynominal Regression: " + x1name)
plt.savefig('Fig_04_2a.png')
plt.show()

##### residual plot

plt.scatter(yx1ypredres_test[x1name], yx1ypredres_test['residual'], c = 'green', label = 'Redisual: Test Data')
#
plt.xlabel(x1name + ': Test Data')
plt.ylabel(yname)
plt.grid(True)
#
#plt.legend()
plt.legend(bbox_to_anchor=(1, 0), loc='lower right', borderaxespad=1, fontsize=10)
plt.title("Polynominal Regression, Residual: " + x1name)
plt.savefig('Fig_04_2b.png')
plt.show()

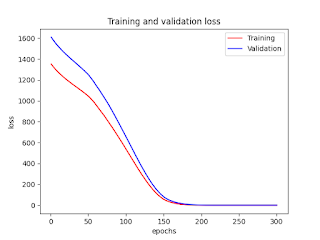
Figures

Fig_02_1.png