Five types of job/work left for humans in the era three of Automation (21st century) - machines take away decisions, in addition to dirty, dangerous, and dull jobs
(1) Step up.
See machines based on higher intellectual ground, design, evaluate, apply, and expand machines
(2) Step aside.
Jobs that need human intelligence and/or hands. Understand humans subtle feeling and care. Do fine-tuning by hands.
(3) Step in.
Jobs that bridge new technologies and business including entrepreneurs.
(4) Step narrowly.
Non-cost-effective jobs for machines. Very special jobs that can be done by a very few people.
(5) Step forward.
Jobs that produce new systems including IT specialists, data scientists, machine learning engineers, IT consultants, programmers, white hackers, etc.
Reference:
Beyond Automation
by Thomas H. Davenport and Julia Kirby
https://hbr.org/2015/06/beyond-automation
The Financial Journal is a blog for all financial industry professionals. This blog has been, and always will be, interactive, intellectually stimulating, and open platform for all readers.
AdSense
Saturday, December 28, 2019
Monday, December 9, 2019
Checklist: hiring an administrative / operational member
This is my own checklist when hiring an administrative / operational member (neither specialist/creative nor management).
Skills:
1. Careful and passive listening
2. Process streamlining (What needs to be done, how, when, by who?)
3. Operations (Documentation, IT)
Mindset:
1. Not selfish. “For members and/or executive/management of an organization”
2. Mentally stable - be able to manage his/her own feeling by him/herself
3. Can-do (proactive) attitude with caution
4. Be based on objective facts, not subjective opinions (personal preferences) - knowing that acting from a sense of “personal justice” is selfish and cheap entertainment
5. A doer, not a critic
Skills:
1. Careful and passive listening
2. Process streamlining (What needs to be done, how, when, by who?)
3. Operations (Documentation, IT)
Mindset:
1. Not selfish. “For members and/or executive/management of an organization”
2. Mentally stable - be able to manage his/her own feeling by him/herself
3. Can-do (proactive) attitude with caution
4. Be based on objective facts, not subjective opinions (personal preferences) - knowing that acting from a sense of “personal justice” is selfish and cheap entertainment
5. A doer, not a critic
Friday, August 23, 2019
My own principled approach
My own principled approach, based on my portfolio management career:
1. Accept reality
2. Don’t make an emotional decision - be objective
3. Make a right decision, rather than focusing on making a short-term profit / win
4. Play a game from a long-term perspective
5. Don’t have a big ego
6. Don’t stick to realized losses and/or profits
7. Analyze, improve, and then repeat this process over and over again
Hope you like this.
Sunday, August 18, 2019
[Financial Analysts Journal] The Impact of Crowding in Alternative Risk Premia Investing
Nick Baltas (2019) The Impact of Crowding in Alternative Risk Premia Investing, Financial Analysts Journal, 75:3, 89-104, DOI: 10.1080/0015198X.2019.1600955
To link to this article: https://doi.org/10.1080/0015198X.2019.1600955
To link to this article: https://doi.org/10.1080/0015198X.2019.1600955
The analysis shows that divergence premia, such as momentum, are more likely to underperform following crowded periods. Conversely, convergence premia, such as value, show signs of outperformance as they transition into phases of larger investor flows.
[Financial Analysts Journal] Are Passive Funds Really Superior Investments? An Investor Perspective,
Edwin J. Elton, Martin J. Gruber & Andre de Souza (2019) Are Passive Funds Really Superior Investments? An Investor Perspective, Financial Analysts Journal, 75:3, 7-19, DOI: 10.1080/0015198X.2019.1618097
To link to this article: https://doi.org/10.1080/0015198X.2019.1618097
In the last ve years, passive funds have increased from 16.4% of the assets under management to 26%.
An investor seeking to use passive portfolios to beat an active fund and attempting to use the Fama–French (market, small cap, value) or Carhart (these three plus momentum) methodology does not have an easily implementable strategy.
(1) the authors searched for a parsimonious set of indexes that correctly price other indexes and (2) the authors show that exchange-traded funds (tradable assets)—rather than indexes—can be used to construct a set of portfolios that outperform active mutual funds. ETFs can be bought and shorted.
The authors found that a combination of five ETFs captures most of the variation in all available ETFs. Five ETFs consist of CRSP Market, Russell 1000 Growth, Russell 1000 Value, Russell 2000 Growth, and Russell Midcap Value
Investors can outperform active funds by buying the lowest-cost ETF that matches each fund’s benchmark, but they can do significantly better by using the five-ETF model the authors developed in this study.
[Financial Analysts Journal] Choosing and Using Utility Functions in Forming Portfolios
My own summary for the paper "Choosing and Using Utility Functions in Forming Portfolios" on Financial Analyst Journal, Volume 75 Number 3, Third Quarter 2019:
- Utility functions and related analysis should be tailored (i.e., purposefully selected) to reflect the investor's circumstances. In this article, it is illustrated for four investor types (a private investor, an endowment fund, a defined-benefit fund, and a retired individual).
- Limitations of mean–variance analysis (essentially a single-period approach ): (1) portfolio return and risk over a discrete horizon (a problem for long-term investors under various economic and market conditions), (2) diversified investor objectives, e.g., delivering a real return, a required income stream, or sufficient assets to cover liabilities, and (3) return distributions are highly (negatively) skewed (and even with high kurtosis).
- Analyzing the mean and variance of his or her portfolio returns over some discrete time horizon is only vaguely relevant to the main concern—namely, the stream of income that can be drawn (from total assets) over time (and total liabilities).
- Choosing a utility function (with parameters) that is fit for a purpose seems more important than seeking validation from an unsettled literature (for functional forms and parameters).
- Advantages of utility functions: (1) available for return distributions of any shape, (2) considerable flexibility in available functions that can encapsulate a wide range of investor objectives and preferences (various time horizons, both up and down-sides of markets, combined strategies in investment and withdrawal in a dynamic framework)
- Utility functions: power utility and two variations of reference-dependent utility
Reference:
Geoffrey J. Warren (2019) Choosing and Using Utility Functions in Forming
Portfolios, Financial Analysts Journal, 75:3, 39-69, DOI: 10.1080/0015198X.2019.1618109
https://doi.org/10.1080/0015198X.2019.1618109
Saturday, August 3, 2019
R: Stepwise Regression
EQ_z.csv
EQ_readme.txt
| SR,InstAUMNetFlow,Views,PassedScreens 0.166649,-0.156857166,-0.339654666,-1.707072202 0.154196,-0.291437111,-0.563715913,-1.665988363 -0.337022,-0.500222653,1.279987797,-0.017351088 1.247881,-0.581146411,-0.057977701,-0.779269670 0.501430,-0.509905650,-0.493296583,0.271775086 0.450267,-0.00902609893963425,0.114869456,-0.220068958 0.063694,-0.169655731,-0.083584568,1.192730775 -0.929903,-0.285324230831457,-0.602126250174628,-0.432616065 -0.509550507810622,-0.338434174,0.620607668,1.785622952 0.365224,-0.186896294,2.233848148,1.693394970 -1.580300,-0.233611745,-0.192414378,0.614118131 -0.482395,-0.169307101,-0.499698211,0.083536853 -0.514293,-0.165160241,-0.570117541,-1.113417949 -0.595051,-0.159739478,-0.589322781,-1.060947977 1.016973,-0.285852677,-0.422877253,-0.824485627 0.610773,-0.231633552,-0.461287732,0.714046898 -0.064182,-0.380821894,0.895882650,1.899020903 0.512515,-0.145408384,-0.218021245,1.154076782 -0.504917,-0.076575250,-0.602126250174628,-0.012381866 0.107556,-0.262600275,-0.493296583,-1.370406874 -1.022209,0.170890895,-0.512501823,-1.198996834 -1.724111,-0.156606065,-0.563715913,-1.367083438 1.166195,0.326738355,-0.083584568,1.734931596 0.809593,0.788629318,0.851070543,0.342095777 -0.649458,0.009107495,-0.256431724,0.921755174 -1.377667,-0.140383296,-0.320449427,-1.526152862 0.990153,1.411729505,-0.025968850,0.159684956 -1.614842,-0.211492345,-0.454886104,0.833875622 -0.264585,-1.069441697,-0.544510674,0.687914906 -1.241969,-0.985389063,-0.211619617,0.659963902 0.698007,-0.079714679,-0.448484476,0.257999353 1.089769,-0.162613459,-0.467689715,1.383121871 1.32550406943183,-0.585543466,-0.50610019449971,0.797317866 -0.600755,-0.181037499,-0.480492971,-0.430425758 -0.576928,-0.204406704,-0.352457922,1.217210296 0.082060,-0.447691794,0.703830254,1.369733531 1.747376,-0.240025438,0.102066199,1.511422435 1.04311685392753,-0.123980924,0.953498724,-0.047212071 0.970067,-0.199495276,0.242904505,1.674865264 -0.827666,0.118408847,-0.032370833,-1.451344886 1.611067,0.003951596,-0.525305434,-0.664270486 -0.265309,-0.291181306,-0.525305434,0.325396378 -0.283334,-0.450520959,-0.595724515499817,-0.409069499 -0.914353,-0.137189795,-0.173209138143544,-0.018567852 0.620408,0.116871706,-0.141200287,-0.515058937 -0.916319,-0.135987571,0.537385082,1.587913661 -1.118505,0.463280152,0.223699265,-0.033130971 -0.187776,-0.146433596,0.793454824,-0.003651244 0.438049,-0.368254819,0.530983098,0.614541695 -0.756349,-0.351659291,-0.410073997,-0.792100537 -2.007125,-0.340248485,-0.461287732,-1.092968001 1.213043,12.4498941614487,0.659018147,-1.629365689 1.481931,0.020246936,1.440031342,0.359641373 0.470195,-0.170614099,4.10956035415073,1.52176147007119 -0.098040,-0.243894430,4.51287074079907,0.668089908 0.958451,-0.521371297,-0.128397031,-1.091215545 1.526234,-0.585420110,-0.121995047,-0.338415089 -0.158304,-0.172770980,-0.557313929687203,0.954070028 -1.594917,-0.146478676,-0.454886104,0.584381433 0.184019,-0.216141007,-0.288440576,-1.142214482 0.193652,0.109340445,0.338930702,1.287215772 -0.025796,0.228702088,0.140476679,-0.910990804063595 -0.039563,-0.155894975,2.957245624,1.349714518 -0.069569,-0.179328085,-0.057977701,-0.262345150 0.664437,0.422490684,-0.365261533915373,-0.239523500 -0.093190,0.132424983,-0.077182940,-1.041415129 -0.627599,-0.245360205,5.153045275,2.428240960 -0.496841,5.156746073,0.466965751,-0.967271399 0.687281,-0.285607501,-0.62133152530456,-0.081582118 -0.046337,-0.264507667,-0.595724515499817,0.296519072 -0.516874,-0.278610357053612,-0.602126250174628,-0.351638819 1.212922,1.297108576,-0.352457922,-0.287037727 -0.555899,-0.153226884156467,-0.518903451,-1.436791707 -0.428942,-0.219646387,0.050852109,-0.183548979 1.671753,-0.240744285845635,0.082860960,-1.528688720 1.455031,0.086150665,0.812660064,1.330511103 -0.848843145917255,-0.238634721002062,-0.486894955,-0.144817964 -0.342203,-0.402923296,-0.006763610,0.722149688 -0.261341,-0.149054440,-0.499698211,0.591711257 0.145620,-0.148280710,3.226119334,1.419738418 -0.648728,-0.110501277,-0.371663162,-1.858500602 0.165561,-0.192266479,-0.0515760726638822,0.724504575 1.316033,0.287768037,2.765193228,0.608901887 1.07672117033893,-0.047766335,-0.314047443,-0.545639758 0.043489,-0.501971986310643,-0.422877253,-0.990917819 -0.335564,-0.098984794,-0.627733259979371,0.253520512 0.275134,-0.154490127,-0.467689715,0.671275591 -1.071435,-0.268930969,0.230100893,0.839687754 -1.677718,-0.367618028,-0.50610019449971,-0.736077500 -2.792272,-0.000985566,-0.205217989,0.713414334 -3.162712,0.554435563,-0.499698211,0.664862878 -0.476443,3.616921479,0.242904505,-0.502830936 -0.446883,0.240895436,-0.576519169,0.378166883 0.804497,1.80429838316979,0.441358528,-1.102479911 0.810396395383469,-0.209836082,0.659018147,1.230376055 1.512610,-0.283147993,-0.442082492,0.261949023 -1.125775,-0.177942350,-0.576519169,-1.538362044 -0.235747,-0.320532243,-0.50610019449971,0.563469366 -0.058605,-0.217158234,-0.422877253,1.147833714 -0.405116,-0.523915691,-0.365261533915373,0.304939696 0.558427,2.104307446,-0.589322781,-1.045967109 0.149047,-0.140040407,-0.614929755077,-1.901264881 0.221256,-0.343111123,-0.333252683,0.588021430 0.707488,-0.014892809,-0.589322781,-0.937741730 -0.439462259823633,-0.217419091,-0.403672013,-0.427858664 -2.666662,-0.191603729,-0.582921153,-0.616014648 -0.682666,-0.359022633,2.073804603,1.323476645 0.495517,-0.143849653,0.556590321,1.261554434 0.056090,0.629195981,-0.378065145,-1.342782390 -0.152172,-0.154590226,-0.454886104,0.609973799 -0.922913,-0.731770140,-0.614929755077,-1.672240955 0.503033,0.327271595,-0.474091343,-0.371997143416322 0.733606,4.334808131,-0.582921153,-1.114098241 -0.452835,0.054434454,-0.570117541,-1.151455365 0.646877,0.262949594,-0.461287732,1.027046109 0.338956,-0.508091644,-0.557313929687203,0.848812018 2.517237,0.172267272,0.057253737,-1.440530678 2.073795,-0.000422336,0.703830254,1.905521730 0.204219,-0.236326787,0.082860960,1.181597124 0.137541,-0.199108968,-0.346056294,0.390286333 -0.188497,0.269261788,-0.371663162,-0.139886013 -1.109823,-0.404126300,0.742240734,-0.815656001 -0.285400,-0.155012302,0.121271439,-0.517587686114939 0.045143,2.240875225,-0.538108690,-0.126841353 -1.334375,0.046212598,-0.371663162,1.201494118 -0.606802,0.019858054,-0.205217989,-0.248800259 -0.396725,-0.121030907,-0.429279236,1.320175759 -1.415686,0.211087536,-0.314047443,-1.711763381 -0.278711,0.226959336,-0.269235336,0.467789822 -0.096545,0.025187559,-0.50610019449971,-0.802137391 -0.516295,-0.057066761,-0.614929755077,0.779983516 -1.027395,0.094618509,-0.627733259979371,0.798629852 -0.545422,-0.015447395,-0.614929755077,-0.630656781 0.051858,6.624260555,-0.582921153,-1.123805035 -0.900951,-0.697362531,-0.563715913,0.263159810 -1.202283,0.115722825,-0.570117541,-0.515427876 -0.362307,-0.011262018,-0.627733259979371,0.283113289 -0.800682242758461,-0.224438992,-0.614929755077,-0.056554092 -0.652601,-0.387034906,-0.461287732,-1.791301809 -1.098117,-0.160149396,-0.147602271,-0.493400062 -1.63154368233283,-0.020919705,-0.557313929687203,0.281200510 0.244335,-0.176245011,-0.62133152530456,-1.460966125 1.465025,3.243307428,-0.614929755077,-1.135711218 -0.533428,-0.008721523,-0.62133152530456,-1.415419239 0.832427,-0.187895057,-0.614929755077,-1.556425900 0.503868,-0.203795809,-0.538108690,-0.240448608 -0.404268,-0.195043593,0.159681918212622,0.177761623 -0.342691339214384,0.367135767,1.011114443,-0.117205240 -1.363586,-0.714729981,-0.378065145,1.062625204 -0.0291831451466879,-0.163401047125453,-0.486894955,1.42436296959336 0.025463,-0.308040187,-0.282038948,-0.182677888 0.296520,-0.269652846,0.306921851,1.448246522 0.293719,-0.15204142156903,-0.365261533915373,-0.464952356 0.516443,-0.364967486,2.592346072,1.269076755 -2.058593,-0.212214199,-0.448484476,0.647099626 0.169856,-0.555138522,-0.230824857,-0.128908681 -1.959894,-0.218208718,-0.205217989,-0.805760065 1.17412613465405,-0.186229521,-0.486894955,0.537748894014036 -0.252419366590358,0.060113992,-0.544510674,1.282120303 0.042213,-0.139898112,-0.326851055,1.22619732272138 1.072650,-0.058675634,-0.224423229,-0.520257100881839 -0.131594,-0.374633821,-0.166807510,0.992511047 -0.193004187652273,-0.661820519,-0.416475625,-0.299986538 -0.869399,-0.369654087,-0.294842203623205,-0.044698105 -1.091420,-0.160339150281318,-0.493296583,-0.34309811719161 0.270032647051064,0.700990534,-0.62133152530456,-0.911526729601099 -0.045317,-1.174445386,-0.62133152530456,-0.840226033 2.3578064780604,-1.045646381,-0.557313929687203,-0.385457004 2.816186,0.065752922,-0.467689715,-0.084547627 0.218480,-0.250210386,-0.493296583,1.367042356 1.626564,-0.188026043,-0.557313929687203,0.178146145 -0.172926136966215,-0.149647665,-0.531707062,0.137729037 1.043252,-0.031921372,-0.50610019449971,0.878338724 -0.010146,1.362271028,-0.525305434,-1.102339316 0.026737,-0.043280690,-0.333252683,0.122800457159431 1.777929,-0.346557692,-0.179610766,-0.536432001 1.828100,-0.116434520,5.895648346,0.809680788 0.241189,-0.212997497,0.070057348,-0.836881342 0.390361,0.164100943,-0.275636964,0.110697408 -0.045645,-0.161859510,-0.570117541,-1.730992591 -1.088554,2.752605111,0.370939554,-0.617332944 0.288309,-0.083579066,-0.166807510,1.574413303 0.409491,-0.127920567,-0.442082492,0.037301354 -0.760782,0.071530230,1.478441821,1.418339733 -0.194476,-0.159968112,-0.544510674,1.356441840 -1.480631,-0.233582892,-0.531707062,0.686630040 -0.0215217837006922,-0.492219079,-0.518903451,-0.096512367 -1.203155,-0.406431609,0.166083546,0.534807512 -1.102299,-0.405891429,-0.435680864207542,0.772658759 -1.239126,-0.392437527,-0.013165594,0.405595217956958 -1.258811,-0.338175110,1.100738657,1.307767182 -0.0571074866929552,-0.631279907,0.422153289,-0.609279682 1.346689,-0.155446548,3.424573357,-0.186056969235076 -0.0816502618078865,0.399860313,1.996983645,0.830684509 -0.418116121725825,-0.517811055,0.0892625879204542,-0.054680719 -1.193879,-0.281633785,-0.454886104,-1.25341456140632 0.411747,1.622506213,-0.512501823,0.258452483 0.685310,-0.061515460,-0.512501823,-1.459990103 1.312342,0.759407719,7.272023967,-0.942706908 -0.784210,-0.241840120,0.198092397,-0.711260609 -0.835663,-0.244683603,-0.294842203623205,-1.057384345 -0.713810,-0.117720186,-0.192414378,-1.668115916 -0.939669906783922,-0.153969315,-0.147602271,1.16188089896552 1.115271,2.750537316,1.164756360,0.824033551 -2.451241,-0.247460359,-0.576519169,-0.0681878322310263 -0.320235624631293,0.204411186,3.354154027,2.551125835 0.663240,-0.0532670453316889,-0.602126250174628,-1.748162928 -0.120364,-0.637703869931426,-0.435680864207542,-0.148486314 0.017253,-0.244514746036811,0.204494025,1.175791069 -1.019264,-0.049853329,1.97777840555593,0.366614350 -0.835251,-0.179186037,1.683297828,1.15894766726893 -0.464607,-0.017757235,0.108467827,0.537597611 0.044342,-0.382634065,0.569393577,-0.094373922 0.109894,-0.511323338,-0.486894955,-1.32972863894046 0.191216,-0.267170012,3.296538308,1.552212567 -0.756611,-0.240729359,-0.493296583,0.851676984937539 -0.790173,-0.228603585,3.264529813,-0.941020219 -1.199834,1.049973503,-0.109191791,-0.621065443 1.497972,1.121229884,-0.083584568,-1.26519855279577 0.499586,0.199358720,0.755044345,1.036440054 0.372367,-0.340695473,0.178887158,1.072409253 0.311203,-0.000079106,-0.576519169,-0.094774138 0.545567,-0.255431323,-0.422877253,0.904930884 0.452658,-0.370998602,2.16983080132776,1.605752519 -0.025794,-0.146901427704502,-0.410073997,0.233828120 -0.325617,-0.156153531449457,-0.614929755077,-0.263386140 0.203416,-0.221852770,-0.147602271,1.243387721 0.128601,-0.170818940,-0.608528020402188,-0.0370282114183059 1.676133,-0.136762779,-0.442082492,0.738883366127731 -0.689085,-0.151702576,-0.480492971,-0.764820380 -0.673910,-0.129172625,-0.627733259979371,-1.912756834 0.974111763938075,0.054761779,0.562991949,-1.179019107 -0.198597,-0.297664641,-0.371663162,0.714594280 -0.371619583294954,0.345718689,-0.531707062,-1.649571416 0.388533,-0.157785535,-0.525305434,-0.588097943 -0.857524,-0.819750999,-0.467689715,0.347405212 -1.856405,0.104352887,-0.371663162,-0.895469935 -1.082708,0.590901176,-0.333252683,0.923876479 0.215122,-0.301174877,-0.62133152530456,0.815355288900369 0.254652,-0.191463154,0.537385082,1.530271189 0.037848,-0.234846224,0.300520223,1.429582803 -0.142788,-0.287995145,0.370939554,1.475348589 0.806460040709491,-0.222282352,-0.531707062,-0.304471637989094 -0.381605771662493,-0.251782626,0.159681918212622,0.428048172263782 1.306665,0.077742335,0.684625015,1.780265143 0.972270,0.687741540,-0.582921153,0.265497902 -1.11337146370607,-0.544544558,-0.550912302,-0.709958764510182 -1.304052,-0.177799093,-0.250030096,0.381748271 0.967195,0.034682666,1.023917699,-0.079014671 -0.103158,-0.363937505,0.146878307,0.597364715 -0.931717941972734,-0.207541263,-0.550912302,-0.636814373 -0.734726,-0.410900303,-0.512501823,0.873959090 -0.089697,-0.771316999,-0.109191791,0.492869701 0.223692,-0.264803867,-0.512501823,-0.150589367 0.737930483499447,-0.166002689,0.223699265,0.577656569 0.590394,0.677136447473134,-0.589322781,-1.043926244 0.524931,0.686809722,-0.595724515499817,-1.014711932 0.732996,-0.879252681,-0.243628468435712,0.594081817 -0.468198,-0.574295968,-0.454886104,1.302082377 -2.711148,0.150427943,0.550188338,-1.232840875 1.425062,-0.298976733,-0.531707062,-0.288633653 -0.110003,-0.151505624,-0.205217989,-1.264449845 -0.744926,-0.885666340,-0.429279236,-0.854629426 0.740105,-0.242456166,-0.608528020402188,-0.249465849 -0.677305,-0.010549902,0.178887158,0.590159641 -0.084509,2.357534389,-0.461287732,-0.511695781 -0.433706,-0.0172512210161253,-0.557313929687203,-1.549619231 -0.499007,-0.155567758,-0.531707062,0.047515235 -0.408959,0.527399709,0.204494025,0.520988955 -0.184534,-0.486048762,-0.480492971,0.185771374 -0.708437,1.897217469,-0.352457922,-1.104250184 -1.84439743809279,-0.198061101,-0.154003899,0.197852238 -1.502775,-0.341208777,3.091682657,-0.545238572 -1.829733,-0.818619480,-0.173209138143544,-1.021210029 -0.384179,-0.116631443,1.638485721,-0.519112050 0.732385,-0.141731222,-0.467689715,0.232170988 -1.111414,-0.187412706,-0.326851055,-0.188490860 1.108479,-0.317224465,-0.608528020402188,-0.541438739 -0.009665,0.026959857,-0.057977701,0.849520876 1.250764,-0.471297921,-0.422877253,0.331138779677439 0.492947,-0.702836291941178,-0.186012750,-0.728984576 -0.545842,-0.157233154,-0.442082492,0.409378731 -1.882971,-0.112367342,-0.486894955,0.679356863 -1.970670,-0.162827871,-0.557313929687203,0.032802947 -1.049814,-0.527002875,0.364537570,0.596416410 -0.959943,-0.680136478,0.761445973,0.383040437798008 1.741447,0.253355419,3.783071281,0.596550128 0.757488,-0.0336197525777512,0.153279935,1.971786223 1.097444,1.471448178,0.210895653400116,-1.064515300 0.178934,-0.161106559,-0.237226485,-1.108048521 0.670503,-0.235137977,-0.346056294,0.063795308 0.395771,-0.219854668320109,-0.333252683,0.174014786 -0.399063,-0.302874336,-0.416475625,-0.759541341 0.405636,0.045509736,0.070057348,-0.354785794 0.573560,0.236871863013435,-0.218021245,-0.609116659 -0.704099,-0.127951753,1.427228086,0.939933698 -0.670001,-0.148836488,0.268511372,0.171417842 -0.381476,-0.152078983065247,-0.339654666,0.042513887 0.875449,-0.003474752,0.281314983692284,1.58808205310127 2.031020,-0.190591743,2.329874346,1.938944039 2.040787,-0.007465437,0.121271439,-0.445784534 1.467411,0.186648828,-0.294842203623205,-1.282044037 0.695175,-0.094302346,-0.448484476,-0.799534754 -2.415240,-0.944593737,-0.531707062,-1.690336441 0.433555,-0.262029262,-0.442082492,0.962542445 1.157393,-0.109842424,0.236502877,-0.432336302 0.695518,0.297248393,-0.371663162,-0.492354158 -1.202278,-0.022344937,-0.531707062,-1.687989370 0.714938,-0.216532737,1.804931249,1.628805963 -0.178556,0.336258295,-0.371663162,0.604285748 0.522765,-0.253688730,-0.589322781,-0.397326572 1.665190,2.558613987,-0.576519169,-1.297565270 1.630445,2.849634370,-0.230824857,-1.213861801 0.935602,-0.186558306,1.075131790,0.628096434542784 -0.102339,-0.161678686,0.537385082,0.378207643 -0.829830,-0.160956954,-0.390868402,0.446230093 -1.46909640118997,-0.215211091,0.415751661,-1.413657976 -3.262978,-0.954704897,-0.198816006,-0.954171771 -0.15181776525811,-0.126891266,-0.179610766,-0.075594434 0.0620927300116409,-0.155963942,-0.518903451,-1.141563848 -1.20480584979087,-0.151044754,-0.416475625,-1.635384719 1.268614,-0.295772934,1.126345881,1.254622945 1.059076,-0.315136105,4.51287074079907,1.926750358 1.530604,-0.476441124,-0.346056294,-0.450292315 1.231314,-0.188197992,0.492572619,2.07821295566167 0.525074,-0.138420952,-0.013165594,0.407384249 0.499150,9.885039821,-0.499698211,-1.305134136 0.668022,-0.202565847,0.767847957,0.898125125 1.627578,-0.111744925,0.646214536,0.050228748 -1.254800,-0.268904897,-0.365261533915373,0.081133005 0.389032,-0.145988773,-0.077182940,1.184405172 0.364970,-0.351282286,0.819061692,1.614247869 0.479758,-0.308561781434144,-0.614929755077,-1.535290776 -0.23936863364442,3.301936435,-0.486894955,-0.119445935 -0.334578,-0.468379535,-0.480492971,-0.208696890771871 0.877980,1.534519813,-0.365261533915373,-0.269124406 -1.132144,-0.385541339,-0.499698211,0.223659368 0.295220,-0.193518849,-0.557313929687203,0.759138085 2.137764,0.008422585,3.14929837529159,2.214355303 0.114446,0.023807521,1.721708308,1.744185159 1.522818,-0.086887448,-0.218021245,-0.054958632 1.704026,-0.661284316,-0.352457922,-1.098737694 0.874527,1.138119296,0.082860960,0.168140476 -0.044894,-0.523755093,-0.62133152530456,-1.542571527 -0.026520,-0.752482262,-0.62133152530456,0.150502266 0.341862,-0.077074292,-0.544510674,1.061609919 2.464107,-0.0967605931637365,-0.570117541,-0.815210121 0.442809556902141,-0.244984842,-0.595724515499817,0.826127989 0.795623,-0.133124653,-0.544510674,1.015308288 0.441996,-0.181847248,-0.595724515499817,-1.411553457 1.420904,0.0497824856575289,-0.390868402,-0.669942610 0.942824,-0.124075659,-0.563715913,-1.016109787 0.564649,1.219310017,-0.608528020402188,-1.373670832 -0.247445,-0.157315103,-0.531707062,0.214442652 2.276633,-0.154364459,-0.454886104,-0.438763505 0.434580,-0.207871502,-0.307645815,0.710767772 -0.968751,-0.306200221,-0.525305434,-1.02386551953021 0.614313,-0.190117472,-0.416475625,-1.262056472 -0.291471,-0.197292298,-0.333252683,-0.054035980 -0.056669,-0.254420769,-0.243628468435712,-0.069056507 -0.380715,-0.149527323,-0.499698211,-0.329408749 -0.413120,-0.275988802,-0.62133152530456,-1.390418546 -1.371689,-0.152792445,-0.557313929687203,-1.49994334219897 -0.313005,-0.516142469,-0.557313929687203,-0.171501404 -1.674759,3.229295134,-0.525305434,-1.609434729 -0.047441,-0.065027251,-0.570117541,-1.103667633 -0.909167,-0.200667048,1.433629714,1.186109911 -0.235025,0.153613918,-0.480492971,-0.650551924267985 -1.477054,0.125802842,-0.480492971,-0.155299080 -1.818330,-0.16549222663597,3.39256450625091,1.316282381 -0.699647,-0.498381882,-0.173209138143544,0.396019644254124 -0.387011,-0.793298583,-0.429279236,0.953868551 -1.097578,-0.943316958,-0.237226485,-0.897277916 -1.451673,-0.952958736,-0.544510674,0.964119552 -1.415615,-0.299479029,-0.518903451,0.338227265 1.664279,-0.077347546,2.656363774,-0.867307928 -0.249136,-0.506432126,-0.595724515499817,-0.982377845 2.146229,-1.215952396,-0.243628468435712,-0.855057974720736 -1.824158,-0.296217838,-0.378065145,-1.559108146 -0.330858,-0.313921034,0.300520223,0.785759104 0.064679,0.357159130,0.178887158,-1.334002443 0.51350543010726,0.034647657,0.313323835,1.527808237 -1.048691,-0.896226492445245,-0.595724515499817,-1.187308763 -0.925660,0.051368953,-0.397270385,-0.701186634 1.822954,-0.136347992,-0.50610019449971,-1.321816366 1.688174,0.184423989,0.018843257628286,-0.461230950 0.877208750890101,-0.163504278,-0.243628468435712,-0.093275336 -0.408265,2.245431536,-0.480492971,0.567443537 1.147235,-0.459170076,-0.186012750,-0.106288467 0.092168,-0.415775037,-0.525305434,0.093621374 1.400327,-0.370769775,-0.326851055,2.236338938 0.961243,-0.057604391,-0.173209138143544,-0.667896012 1.074359,-0.244973639,-0.038772461,1.170851190 0.952095,-0.047662769,-0.435680864207542,-1.024253702 0.810367,-0.199987524,-0.531707062,0.531896991616595 0.911688,-0.155212479,-0.557313929687203,0.453788959 -0.687500,-0.207219748,1.612878498,0.934943523 -0.494756154673527,-0.721022599,-0.544510674,-0.434739999 -1.076658,-0.236241117,-0.467689715,-0.840005859 -0.507938980058189,-0.181331877,-0.512501823,1.074266427 -0.854066,-0.157575763,-0.282038948,-1.280770496 -1.140147,-0.195392347,0.831865303,1.123117466 -0.967197971014018,0.379356455,1.721708308,-0.115265604 -0.860956,-0.159196533,-0.211619617,-1.583913733 -0.440717,0.036285937,-0.346056294,1.749574497 -0.388028,-0.291306205,-0.493296583,-1.434824405 -0.561796,-0.188054601,-0.570117541,-1.380435112 -1.551181,-0.160951457,-0.563715913,-1.666234332 -0.114021,-0.154703671,-0.474091343,0.145694155 -0.306305,-0.222529972,-0.589322781,-0.048007061 0.161680,-0.202047413,-0.442082492,-0.670846241 -0.565885,-0.129611968,-0.403672013,1.034105047 -0.515516,-0.546654995648727,-0.288440576,0.365140768 -0.502967,-0.075181238,-0.282038948,0.225629835 -1.039492,-0.454758461891068,0.0892625879204542,0.544640037 -1.818037,-0.635297146,0.006039646,-1.055027476 0.821009,-0.349273383,-0.544510674,-0.362321979 0.410191,0.039217295,1.728109936,1.469233244 0.417522,-0.300787745,-0.627733259979371,-1.691315850 -0.704707,1.03632091993901,-0.486894955,-1.18394951112346 -0.359895,-0.087233760,-0.333252683,-0.521366902 -1.525286,-0.130679792,-0.531707062,-0.842573792 1.02240475953559,-0.203252704,0.466965751,1.065821970 -0.674584,-0.593110789,0.018843257628286,-1.227321217 -0.180194,-0.283588894,-0.563715913,-0.931897957 0.636734,0.855310804,-0.538108690,-0.070958183 -1.299804,-0.096556794,-0.525305434,-0.403833243822609 -0.016008,-0.666014835,-0.544510674,-0.447313216 -0.170290,-0.248346111,-0.147602271,0.792481299 -0.108623537795341,-0.108304165,0.716633866,1.238095850 -0.108145,-0.327844039,-0.614929755077,0.083448133 0.149448,-0.148195861,-0.550912302,0.423497366 -0.106037,0.0130674210538852,2.803603707,0.131235177 0.545910,-0.252934693,5.293883935,1.204003868 1.838081,1.391232466,0.198092397,-1.273305670 0.201479,-0.152505536,-0.550912302,-0.420579794 0.304702,-0.148996574,-0.614929755077,-0.520865346 0.560499,-0.161948560,-0.563715913,-1.002763229 0.127568,-0.365445542,-0.314047443,0.965878824 0.123632,-0.238246080,-0.269235336,1.246399309 0.292211,0.829398027702751,-0.154003899,1.693279797 0.920194,-0.014924300,-0.582921153,-1.119227887 0.651954,1.938659887,-0.538108690,-0.972557788 1.105303,-0.196373031,-0.070781312,-0.0897229382163552 -0.083019,-0.109429821,0.684625015,0.559897837 -1.581478,-0.267792660,-0.50610019449971,-0.012037053 0.103057,0.450195832,-0.544510674,-0.605625438 0.654057,-0.238170020,-0.595724515499817,-1.385036498 0.809953,-0.267373864,-0.486894955,0.305502701 -0.974830,-0.195544737750197,-0.371663162,-0.434309367 -1.351973,-0.338456215,0.332529074,0.757216084 -0.921372,0.024699722,-0.346056294,-1.502862458 -0.735370,0.381299360,-0.499698211,-0.201082127 -0.329823,-0.475889069,-0.275636964,-1.821750711 -0.227863,-0.121992821,1.472040193,0.453775257 1.916520,-0.152060200578572,-0.474091343,-0.741558147617734 -0.168374,0.085463446,-0.525305434,0.499786386 0.799647,0.036271866,0.300520223,0.841545160973985 0.494246352541292,0.071703013,-0.365261533915373,0.475471829 -0.821204,-0.241263981,-0.570117541,-0.510147290 2.03314968216439,-0.343729374,-0.371663162,0.615231603 0.848775,-0.471221233,-0.563715913,-0.701784039 -0.531753,1.012318558,-0.057977701,0.718696123 0.172966,-0.423786741,-0.480492971,-0.309795381 -0.528577,0.204569690,-0.057977701,-0.858220047 2.012559,-0.728330487,-0.186012750,-0.235091173 1.603728,-0.085330973,0.082860960,-0.927695805303649 1.548838,-0.029998010,2.445105783,0.482108781 0.949720,-0.951233525,-0.307645815,-0.595318235 0.215603,0.151540844,0.895882650,2.178508538 0.457194,-0.254290572,1.491245433,0.721525699 -1.445906,-0.189058693,-0.230824857,0.592648661 -0.493205,0.091922688,-0.454886104,-0.332288206 -0.101620,-0.387226194,-0.314047443,1.61735137353699 -0.319855,0.453043988,-0.243628468435712,-0.619507396 0.454695,-0.526448068,-0.166807510,-0.528845186 0.533224,-0.511902980,-0.589322781,-2.071079683 1.057605,-0.069010180,0.639812908,-0.361525836 0.735009,-0.147428812,-0.493296583,-1.529903036 0.143570,-0.416016747,-0.403672013,-0.991399009 1.070312,-0.412127416539272,-0.602126250174628,-0.521141206 0.012265,-0.546924244,-0.589322781,-1.712352161 2.492121,-0.402826384,-0.538108690,-1.634800884 -1.986114,-0.410855849,-0.397270385,0.222345269 0.094664,-0.241031635,-0.474091343,0.897479133 -1.335527,-0.498889435,0.076458976,1.454588027 -1.915453,-0.373366040,-0.480492971,-0.376311031 0.541208,-0.191442915,-0.230824857,0.917916461 0.275911,-0.237416440,-0.352457922,0.852711463 0.465545,-0.151577739,-0.602126250174628,0.394784487567216 0.248552,0.435357237,-0.301244187,-0.407157317 -0.703010,0.0331906461883284,-0.147602271,-2.460426633 -0.712809,-0.332667635,-0.000361982,0.871785639 -0.929787,-0.097169153,-0.282038948,0.216550083 -1.107520,-0.056195503,-0.397270385,-0.401844040 -0.005100,-0.191880111,-0.480492971,-0.864570896 -0.647156,-0.227929866,-0.550912302,-0.423969655 -0.876038,-0.239392707,0.940695113,1.026337595 0.546336,-0.154164826,-0.339654666,-1.321754461 0.722542,-0.25495778906871,-0.410073997,0.899924470 0.216564,-0.396342475,0.102066199,1.197443421 -0.170823,-0.240529786,0.044450481,1.01151515860971 -0.255846,-0.429677319,-0.403672013,0.595139046 -0.199170,-0.154668530,-0.576519169,-0.854955269 0.756563,-0.095075528,-0.230824857,0.494108103 -0.266764605435791,0.247520130,-0.614929755077,-1.686967461 0.204927,-0.161542113,-0.262833708,1.694011305 0.714035,-0.625189117,1.171157988,0.147106511 -2.544617,-0.396081644,0.038048497,0.579440018 0.285645973308248,-0.323214741,-0.589322781,0.392991321 -1.689353,0.328752793143277,0.364537570,-1.20682513877873 1.791098,-0.211447185,-0.154003899,-1.179785612 0.755692,0.377971087,-0.512501823,-0.450847968867323 1.093103,-0.180034953,1.587271630,2.29198263070722 1.551543,-1.19420401796333,-0.474091343,0.170128476 1.304110,-0.195374843,5.953264065,2.519789571 0.453232,1.388042988,0.262109744,0.089148995 2.15874317290323,0.171647374,1.996983645,1.995051954 -2.004631,-0.547060434,-0.570117541,-0.962753829370595 0.212549,-0.215911574,-0.262833708,0.126265883 0.197826,-0.3595151129571,-0.544510674,-1.050309714 0.572398,-0.301820977,-0.570117541,-0.262379439565368 0.116465,-0.668514750,-0.589322781,-0.110644682 0.800450,-0.223934934,-0.461287732,0.489188489 1.379630,-0.266054307,-0.121995047,-0.611487948 2.018530,1.064818149,-0.307645815,-1.373922616 -2.446533,-0.635182916961691,-0.499698211,-0.267967394 0.153731,-0.395597651,0.178887158,1.071482638 0.310769955153565,-0.182106606,-0.378065145,0.751844634 2.951171,-0.410083036,-0.262833708,-0.021675856 -0.072208,-0.203587533,-0.416475625,0.529752936 -0.441732,-0.176422307137254,-0.531707062,0.310237380360702 -0.161622,0.266965478,-0.390868402,-1.670662088 -0.111939,-0.076705160,-0.403672013,1.69949419744063 0.508922,-0.633342468,-0.50610019449971,0.730943983202699 -0.029011,-0.140601673,-0.448484476,-0.750606745 -0.199691,-0.698485003,-0.461287732,1.027599437 0.389439,0.301166133329801,0.947096741,-1.141114570 -0.574762,-0.053329130,-0.525305434,-1.132169832 0.053795,-0.387914951,-0.557313929687203,-1.61369202076382 -0.065107,2.720079780,-0.314047443,-0.534571581 -1.270810,-1.146934116,-0.512501823,0.987897425762039 -0.81357446477793,0.331134138,-0.250030096,-0.224159404 -0.244980,-0.660222161,0.863874155,1.22080328274542 -1.167461,-0.029841975,1.459236581,0.495164180 0.619671,-0.203955602,-0.346056294,0.534920309 1.258805,0.374096587,0.863874155,0.295114047 0.278193,0.128140860,0.134074695,1.730215815 0.592690,-0.497047606,-0.077182940,1.611223560 0.771603,-0.229815998240306,-0.339654666,1.534909200 -0.314994,-0.489528597,-0.070781312,0.781255155893192 -1.733675,-0.599647318,-0.512501823,-0.835398042 1.778214,-0.435126821,-0.582921153,-1.979623727 -2.749096,-0.168136819,-0.595724515499817,-1.408350928 0.791925,-0.488864312,-0.454886104,1.550932423 -0.497820699251925,-1.078584581,-0.416475625,0.429106918 -0.430395,-0.114320656,-0.538108690,1.080621159 1.05320871624604,-0.266050860111263,-0.544510674,-0.690431053575897 1.320083,-0.420999556,0.044450481,1.377347223 -0.696313,4.159591986,-0.186012750,-0.445636214 -0.541551,0.312952216,-0.563715913,-0.578121659 0.388860,-0.125810866,-0.467689715,1.267342399 0.837597,-0.298751852,-0.614929755077,0.503029039 -0.541987,-0.299008729,-0.186012750,-0.508676397 -0.083920,-0.169415736,0.486170991,1.460949018 0.135914,-0.328898445,-0.576519169,0.239521551 |
EQ_readme.txt
# stard R Console on MacOS # get a working directory getwd() # change the working directory setwd("/Users/yoshi/Downloads/") dat <- read.csv('EQ_z.csv') head(dat) # SR InstAUMNetFlow Views PassedScreens #1 0.168106 -0.07055196 -0.33920655 -1.70145662 #2 0.155648 -0.09568507 -0.56343473 -1.66043722 #3 -0.335729 -0.13467625 1.28164263 -0.01438553 #4 1.249691 -0.14978894 -0.05731972 -0.77510918 #5 0.502996 -0.13648457 -0.49296294 0.27428721 #6 0.451817 -0.04294418 0.11565621 -0.21678547 # All the data are expressed in z-score. ########## 1.1 Regression Analysis (SR ~ InstAUMNetFlow) reg_InstAUMNetFlow <- lm(SR~InstAUMNetFlow,data=dat) summary(reg_InstAUMNetFlow) #Call: #lm(formula = SR ~ InstAUMNetFlow, data = dat) # #Residuals: # Min 1Q Median 3Q Max #-3.2166 -0.6249 -0.0146 0.6306 2.9913 # #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) 0.02248 0.04290 0.524 0.6006 #InstAUMNetFlow 0.51079 0.22452 2.275 0.0233 * #--- #Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 # #Residual standard error: 0.9966 on 564 degrees of freedom #Multiple R-squared: 0.009094, Adjusted R-squared: 0.007337 #F-statistic: 5.176 on 1 and 564 DF, p-value: 0.02328 #Multiple R-squared: 0.009094 # InstAUMNetFlow does not explain SR (Sharpe Ratio) very much. plot(dat$InstAUMNetFlow,dat$SR,xlab='Inst AUM Net Flow 1Y (%)',ylab='Sharpe Ratio (USD, 1Y)') abline(reg_InstAUMNetFlow) ########## 1.2 Regression Analysis (SR ~ Views) reg_Views <- lm(SR~Views,data=dat) summary(reg_Views) #Call: #lm(formula = SR ~ Views, data = dat) # #Residuals: # Min 1Q Median 3Q Max #-3.2360 -0.5970 -0.0080 0.6647 2.9892 # #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) 0.001304 0.041664 0.031 0.975047 #Views 0.140832 0.041670 3.380 0.000776 *** #--- #Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 # #Residual standard error: 0.9912 on 564 degrees of freedom #Multiple R-squared: 0.01985, Adjusted R-squared: 0.01811 #F-statistic: 11.42 on 1 and 564 DF, p-value: 0.0007759 #Multiple R-squared: 0.01985 # Views do not explain SR (Sharpe Ratio) very much. plot(dat$Views,dat$SR,xlab='Views 1Y (%)',ylab='Sharpe Ratio (USD, 1Y)') abline(reg_Views) ########## 1.3 Regression Analysis (SR ~ PassedScreens) reg_PassedScreens <- lm(SR~PassedScreens,data=dat) summary(reg_PassedScreens) #Call: #lm(formula = SR ~ PassedScreens, data = dat) # #Residuals: # Min 1Q Median 3Q Max #-3.2178 -0.5859 -0.0177 0.6604 2.9539 # #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) 0.001163 0.041945 0.028 0.9779 #PassedScreens 0.081500 0.042048 1.938 0.0531 . #--- #Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 # #Residual standard error: 0.9979 on 564 degrees of freedom #Multiple R-squared: 0.006617, Adjusted R-squared: 0.004856 #F-statistic: 3.757 on 1 and 564 DF, p-value: 0.05309 #Multiple R-squared: 0.006617 # Passed Screens do not explain SR (Sharpe Ratio) very much. plot(dat$PassedScreens,dat$SR,xlab='PassedScreens 1Y (%)',ylab='Sharpe Ratio (USD, 1Y)') abline(reg_PassedScreens) ########## 2 Multiple Regression Analysis (SR ~ InstAUMNetFlow + Views + PassedScreens) ##### multiple regression (with all explanatory variables) reg_multiple <- lm(SR~InstAUMNetFlow+Views+PassedScreens,data=dat) summary(reg_multiple) #Call: #lm(formula = SR ~ InstAUMNetFlow + Views + PassedScreens, data = dat) # #Residuals: # Min 1Q Median 3Q Max #-3.1985 -0.5797 -0.0276 0.6324 3.0271 # # #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) 0.02399 0.04253 0.564 0.57288 #InstAUMNetFlow 0.55353 0.22643 2.445 0.01481 * #Views 0.11937 0.04466 2.673 0.00773 ** #PassedScreens 0.05587 0.04542 1.230 0.21916 #--- #Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 # #Residual standard error: 0.9872 on 562 degrees of freedom #Multiple R-squared: 0.03122, Adjusted R-squared: 0.02605 #F-statistic: 6.036 on 3 and 562 DF, p-value: 0.0004748 #Multiple R-squared: 0.03122 # R2 is still very small. ##### stepwise regression reg0 <- lm(SR~1,dat) step(reg0,direction='both', scope=list(upper=~InstAUMNetFlow+Views+PassedScreens)) #Start: AIC=1.37 #SR ~ 1 # # Df Sum of Sq RSS AIC #+ Views 1 11.2227 554.15 -7.9799 #+ InstAUMNetFlow 1 5.1412 560.23 -1.8022 #+ PassedScreens 1 3.7411 561.63 -0.3894 #<none> 565.37 1.3683 # #Step: AIC=-7.98 #SR ~ Views # # Df Sum of Sq RSS AIC #+ InstAUMNetFlow 1 4.9513 549.19 -11.0598 #<none> 554.15 -7.9799 #+ PassedScreens 1 0.6017 553.54 -6.5948 #- Views 1 11.2227 565.37 1.3683 # #Step: AIC=-11.06 #SR ~ Views + InstAUMNetFlow # # Df Sum of Sq RSS AIC #<none> 549.19 -11.0598 #+ PassedScreens 1 1.4748 547.72 -10.5818 #- InstAUMNetFlow 1 4.9513 554.15 -7.9799 #- Views 1 11.0328 560.23 -1.8022 # #Call: #lm(formula = SR ~ Views + InstAUMNetFlow, data = dat) # #Coefficients: # (Intercept) Views InstAUMNetFlow # 0.02199 0.13965 0.50131 #As a result of stepwise regression, Views is selected first, InstAUMNetFlow is selected second, and then PassedScreens is rejected. #If you look at a correlation matrix of data, PassedScreens is highly correlated to Views. # cor(dat) # SR InstAUMNetFlow Views PassedScreens #SR 1.00000000 0.09536016 0.14089073 0.08134542 #InstAUMNetFlow 0.09536016 1.00000000 0.01267051 -0.17021810 #Views 0.14089073 0.01267051 1.00000000 0.36147622 #PassedScreens 0.08134542 -0.17021810 0.36147622 1.00000000 ##### multiple regression (after removing PassedScreens) reg_multiple2 <- lm(SR~InstAUMNetFlow+Views,data=dat) summary(reg_multiple2) #Call: #lm(formula = SR ~ InstAUMNetFlow + Views, data = dat) # #Residuals: # Min 1Q Median 3Q Max #-3.1469 -0.6066 0.0004 0.6293 3.0273 # #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) 0.02199 0.04252 0.517 0.605257 #InstAUMNetFlow 0.50131 0.22251 2.253 0.024646 * #Views 0.13965 0.04152 3.363 0.000823 *** #--- #Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 # #Residual standard error: 0.9877 on 563 degrees of freedom #Multiple R-squared: 0.02861, Adjusted R-squared: 0.02516 #F-statistic: 8.29 on 2 and 563 DF, p-value: 0.0002829 ########## stepwise regression (explained variable: InstAUMNetFlow) reg0 <- lm(InstAUMNetFlow~1,dat) step(reg0,direction='both', scope=list(upper=~SR+Views+PassedScreens)) #Start: AIC=-382.15 #InstAUMNetFlow ~ 1 # # Df Sum of Sq RSS AIC #+ SR 1 1.30504 61.456 -385.74 #<none> 62.761 -382.15 #+ Views 1 0.10122 62.659 -380.58 #+ PassedScreens 1 0.00000 62.761 -380.15 # #Step: AIC=-385.74 #InstAUMNetFlow ~ SR # # Df Sum of Sq RSS AIC #<none> 61.456 -385.74 #+ Views 1 0.09613 61.359 -384.15 #+ PassedScreens 1 0.00373 61.452 -383.75 #- SR 1 1.30504 62.761 -382.15 # #Call: #lm(formula = InstAUMNetFlow ~ SR, data = dat) # #Coefficients: #(Intercept) SR # -0.05398 0.07050 reg_multiple3 <- lm(InstAUMNetFlow~SR,data=dat) summary(reg_multiple3) #Call: #lm(formula = InstAUMNetFlow ~ SR, data = dat) # #Residuals: # Min 1Q Median 3Q Max #-0.7203 -0.1332 -0.0501 0.0531 5.9795 # #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) -0.05398 0.02958 -1.825 0.0692 . #SR 0.07050 0.02977 2.368 0.0186 * #--- #Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 # #Residual standard error: 0.4825 on 264 degrees of freedom #Multiple R-squared: 0.02079, Adjusted R-squared: 0.01708 #F-statistic: 5.606 on 1 and 264 DF, p-value: 0.01862 plot(dat$SR,dat$InstAUMNetFlow,xlab='Sharpe Ratio (USD, 1Y)',ylab='Inst AUM Net Flow 1Y (%)') abline(reg_multiple3) |
Saturday, July 13, 2019
Python: Linear and Regularized Logistic Regression
0_runme.txt
##### Open Terminal on Mac OS # Run the following commands on Terminal. #Current working directory pwd #For instance, your MacOS environment goes like this: #/Users/xxx/ #Change your working directory #cd /Users/xxx/Downloads which python3 #For instance, my MacOS environment goes like this: #/Library/Frameworks/Python.framework/Versions/3.7/bin/python3 which pip3 #For instance, my MacOS environment goes like this: #/Library/Frameworks/Python.framework/Versions/3.7/bin/pip3 #Run after connecting to the Internet pip3 install matplotlib pip3 install sklearn pip3 install dtreeviz pip3 install IPython pip3 install pandas pip3 install scipy python3 -V #For instance, my MacOS environment goes like this: #Python 3.7.4 #Starting Python 3 #python3 #You do not use this since you're running py scripts on Terminal, rather than running your scripts on Pyton IDLE. #Download files: #ex1data1.txt #ex1data2.txt #ex2data1.txt #ex2data2.txt # #From: #https://github.com/LilianYe/Andrew-Ng-Machine-Learning-Programming-solutions-/find/master #Running Python py scripts python3 1a_liner_regression_w_one_variable.py python3 1b_liner_regression_w_multiple_variables.py python3 2.1_logistic_regression_or_classification.py python3 2.2_regularized_logistic_regression.py |
1a_liner_regression_w_one_variable.py
| ########## Python Implementation of Andrew Ng’s Machine Learning Course (Part 1) ########## Linear Regression with One Variable # # Reference: #https://medium.com/analytics-vidhya/python-implementation-of-andrew-ngs-machine-learning-course-part-1-6b8dd1c73d80 # #Here we will implement linear regression with one variable to predict profits for a food truck. # #ex1data1.txt #contains the dataset for our linear regression exercise. #column data #1 population of a city #2 profit of a food truck in that city # import libraries import numpy as np import pandas as pd import matplotlib.pyplot as plt ###Reading and Plotting the data data = pd.read_csv('ex1data1.txt', header = None) #read from dataset X = data.iloc[:,0] # read first column y = data.iloc[:,1] # read second column m = len(y) # number of training example data.head() # view first few rows of the data plt.scatter(X, y) plt.xlabel('Population of City in 10,000s') plt.ylabel('Profit in $10,000s') plt.savefig('fig_1a.1.png') # Save an image file plt.show() ###Adding the intercept term X = X[:,np.newaxis] #(*1) y = y[:,np.newaxis] #(*1) theta = np.zeros([2,1]) #set one initial parameter theta to 0 iterations = 1500 alpha = 0.01 # set another initial parameter, the learning rate alpha, to 0.01 ones = np.ones((m,1)) X = np.hstack((ones, X)) # adding the intercept term #(*1) #Note on np.newaxis: # When you read data into X, you will observe that X, y are rank 1 arrays. #rank 1 array will have a shape of (m, ) whereas rank 2 arrays will have a shape of (m,1). #When operating on arrays its good to convert rank 1 arrays to rank 2 arrays because rank 1 arrays often give unexpected results. #To convert rank 1 to rank 2 array we use someArray[:,np.newaxis]. ###Computing the cost def computeCost(X, y, theta): temp = np.dot(X, theta) - y return np.sum(np.power(temp, 2)) / (2*m) J = computeCost(X, y, theta) print(J) #You should expect to see a cost of 32.07. More precisely, 32.072733877455676. ###Finding the optimal parameters using Gradient Descent def gradientDescent(X, y, theta, alpha, iterations): for _ in range(iterations): temp = np.dot(X, theta) - y temp = np.dot(X.T, temp) theta = theta - (alpha/m) * temp return theta theta = gradientDescent(X, y, theta, alpha, iterations) print(theta) #Expected theta values [-3.6303, 1.1664] #Technically, #[[-3.63029144] # [ 1.16636235]] # # So, for instance, the first row of actual data goes like this. # Population (10,000) Profit ($10,000) # 6.1101 17.592 # # An estimated profit for this population is # -3.6303 * 1 + 1.1664 * 6.1101 = 3.49652064 #We now have the optimized value of theta . Use this value in the above cost function. J = computeCost(X, y, theta) print(J) #It should give you a value of 4.483 (4.483388256587726) which is much better than 32.07 ### Plot showing the best fit line plt.scatter(X[:,1], y) plt.xlabel('Population of City in 10,000s') plt.ylabel('Profit in $10,000s') plt.plot(X[:,1], np.dot(X, theta)) plt.savefig('fig_1a.2.png') # Save an image file plt.show() |
| ########## Python Implementation of Andrew Ng’s Machine Learning Course (Part 1) ########## Linear Regression with multiple variables #(also called Multivariate Linear Regression) # ex1data2.txt # a training set of housing prices in Portland, Oregon # column data # 1 size of the house (in square feet) # 2 number of bedrooms # 3 price of the house ### import import numpy as np import pandas as pd ### data loading data = pd.read_csv('ex1data2.txt', sep = ',', header = None) X = data.iloc[:,0:2] # read first two columns into X y = data.iloc[:,2] # read the third column into y m = len(y) # no. of training samples data.head() ### Feature Normalization X = (X - np.mean(X))/np.std(X) ###Adding the intercept term and initializing parameters ones = np.ones((m,1)) X = np.hstack((ones, X)) alpha = 0.01 num_iters = 400 theta = np.zeros((3,1)) y = y[:,np.newaxis] ###Computing the cost def computeCostMulti(X, y, theta): temp = np.dot(X, theta) - y return np.sum(np.power(temp, 2)) / (2*m) J = computeCostMulti(X, y, theta) print(J) #You should expect to see a cost of 65591548106.45744. ###Finding the optimal parameters using Gradient Descent def gradientDescentMulti(X, y, theta, alpha, iterations): m = len(y) for _ in range(iterations): temp = np.dot(X, theta) - y temp = np.dot(X.T, temp) theta = theta - (alpha/m) * temp return theta theta = gradientDescentMulti(X, y, theta, alpha, num_iters) print(theta) # your optimal parameters will be [[334302.06399328],[ 99411.44947359], [3267.01285407]] # For instance, if you look at the sample data in the first row, # 2104 3 399900 # first column's average: 2000.68085106383 # first column's SD: 794.70235353389 # second column's average: 3.17021276595745 # second column's SD: 0.7609818867801 # # So, the first column (2104-2000.68085106383)/794.70235353389 = 0.1300 (SD) # Then the second column (3-3.17021276595745)/0.7609818867801 = -0.2237 (SD) # 334302.06399328 * 1 + 99411.44947359 * 0.1300 + 3267.01285407 * (-0.2237) # = 346494.721649391 (estimated data) ~ 399,900 (actual data) #We now have the optimized value of theta . Use this value in the above cost function. J = computeCostMulti(X, y, theta) print(J) #This should give you a value of 2105448288.6292474 which is much better than 65591548106.45744 |
2.1_logistic_regression_or_classification.py
| ########## Python Implementation of Andrew Ng’s Machine Learning Course (Part 2.1) ########## Logistic Regression or Classification (part 2.1) # # Reference: # https://medium.com/analytics-vidhya/python-implementation-of-andrew-ngs-machine-learning-course-part-2-1-1a666f049ad6 # # ##### Logistic Regression ### import libraries import numpy as np import pandas as pd import matplotlib.pyplot as plt import scipy.optimize as opt # more on this later ### data #ex2data1.txt #column data #1 Exam 1 score #2 Exam 2 score #3 0 (fail) or 1 (pass) data = pd.read_csv('ex2data1.txt', header = None) X = data.iloc[:,:-1] y = data.iloc[:,2] data.head() ### plotting mask = y == 1 adm = plt.scatter(X[mask][0].values, X[mask][1].values) not_adm = plt.scatter(X[~mask][0].values, X[~mask][1].values) plt.xlabel('Exam 1 score') plt.ylabel('Exam 2 score') plt.legend((adm, not_adm), ('Admitted', 'Not admitted')) plt.savefig('fig_2.1.1.png') # Save an image file plt.show() ### Implementation ## Sigmoid Function def sigmoid(x): return 1/(1+np.exp(-x)) ## Cost Function def costFunction(theta, X, y): J = (-1/m) * np.sum(np.multiply(y, np.log(sigmoid(X @ theta))) + np.multiply((1-y), np.log(1 - sigmoid(X @ theta)))) return J ## Gradient Function def gradient(theta, X, y): return ((1/m) * X.T @ (sigmoid(X @ theta) - y)) (m, n) = X.shape X = np.hstack((np.ones((m,1)), X)) y = y[:, np.newaxis] theta = np.zeros((n+1,1)) # intializing theta with all zeros J = costFunction(theta, X, y) print(J) # This should give us a value of 0.693 for J. # More precisely, 0.6931471805599453 ### Learning parameters using fmin_tnc temp = opt.fmin_tnc(func = costFunction, x0 = theta.flatten(),fprime = gradient, args = (X, y.flatten())) #the output of above function is a tuple whose first element #contains the optimized values of theta theta_optimized = temp[0] print(theta_optimized) # The above code should give [-25.16131862, 0.20623159, 0.20147149]. J = costFunction(theta_optimized[:,np.newaxis], X, y) print(J) #You should see a value of 0.203 (0.20349770158947486). # Compare this with the cost 0.693 obtained using initial theta. ### Plotting Decision Boundary (Optional) plot_x = [np.min(X[:,1]-2), np.max(X[:,2]+2)] plot_y = -1/theta_optimized[2]*(theta_optimized[0] + np.dot(theta_optimized[1],plot_x)) mask = y.flatten() == 1 adm = plt.scatter(X[mask][:,1], X[mask][:,2]) not_adm = plt.scatter(X[~mask][:,1], X[~mask][:,2]) decision_boun = plt.plot(plot_x, plot_y) plt.xlabel('Exam 1 score') plt.ylabel('Exam 2 score') plt.legend((adm, not_adm), ('Admitted', 'Not admitted')) plt.savefig('fig_2.1.2.png') # Save an image file plt.show() def accuracy(X, y, theta, cutoff): pred = [sigmoid(np.dot(X, theta)) >= cutoff] acc = np.mean(pred == y) print(acc * 100) accuracy(X, y.flatten(), theta_optimized, 0.5) # This should give us an accuracy score of 89% . Hmm… not bad. |
2.2_regularized_logistic_regression.py
| ########## Python Implementation of Andrew Ng’s Machine Learning Course (Part 2.2) ########## Regularized Logistic Regression (part 2.2) # # Reference: # https://medium.com/analytics-vidhya/python-implementation-of-andrew-ngs-machine-learning-course-part-2-2-dceff1a12a12 # # ##### Regularized logistic regression ### import libraries import numpy as np import pandas as pd import matplotlib.pyplot as plt import scipy.optimize as opt # more on this later ### data #ex2data2.txt #column data #1 test 1 result #2 test 2 result #3 0 (rejected) or 1 (accepted) data = pd.read_csv('ex2data2.txt', header = None) X = data.iloc[:,:-1] y = data.iloc[:,2] data.head() ### plotting mask = y == 1 passed = plt.scatter(X[mask][0].values, X[mask][1].values) failed = plt.scatter(X[~mask][0].values, X[~mask][1].values) plt.xlabel('Microchip Test1') plt.ylabel('Microchip Test2') plt.legend((passed, failed), ('Passed', 'Failed')) plt.savefig('fig_2.2.1.png') # Save an image file plt.show() ### Feature mapping def mapFeature(X1, X2): degree = 6 out = np.ones(X.shape[0])[:,np.newaxis] for i in range(1, degree+1): for j in range(i+1): out = np.hstack((out, np.multiply(np.power(X1, i-j), np.power(X2, j))[:,np.newaxis])) return out X = mapFeature(X.iloc[:,0], X.iloc[:,1]) ### Implementation ## Sigmoid Function def sigmoid(x): return 1/(1+np.exp(-x)) ## Cost Function def lrCostFunction(theta_t, X_t, y_t, lambda_t): m = len(y_t) J = (-1/m) * (y_t.T @ np.log(sigmoid(X_t @ theta_t)) + (1 - y_t.T) @ np.log(1 - sigmoid(X_t @ theta_t))) reg = (lambda_t/(2*m)) * (theta_t[1:].T @ theta_t[1:]) J = J + reg return J ## Gradient Function def lrGradientDescent(theta, X, y, lambda_t): m = len(y) grad = np.zeros([m,1]) grad = (1/m) * X.T @ (sigmoid(X @ theta) - y) grad[1:] = grad[1:] + (lambda_t / m) * theta[1:] return grad (m, n) = X.shape y = y[:, np.newaxis] theta = np.zeros((n,1)) lmbda = 1 J = lrCostFunction(theta, X, y, lmbda) print(J) #This gives us a values of 0.69314718. ## Learning parameters using fmin_tnc output = opt.fmin_tnc(func = lrCostFunction, x0 = theta.flatten(), fprime = lrGradientDescent, \ args = (X, y.flatten(), lmbda)) theta = output[0] print(theta) # theta contains the optimized values ## Accuracy of model pred = [sigmoid(np.dot(X, theta)) >= 0.5] np.mean(pred == y.flatten()) * 100 print(np.mean(pred == y.flatten()) * 100) # This gives our model accuracy as 83.05% (83.05084745762711). ## Plotting Decision Boundary (optional) u = np.linspace(-1, 1.5, 50) v = np.linspace(-1, 1.5, 50) z = np.zeros((len(u), len(v))) def mapFeatureForPlotting(X1, X2): degree = 6 out = np.ones(1) for i in range(1, degree+1): for j in range(i+1): out = np.hstack((out, np.multiply(np.power(X1, i-j), np.power(X2, j)))) return out for i in range(len(u)): for j in range(len(v)): z[i,j] = np.dot(mapFeatureForPlotting(u[i], v[j]), theta) mask = y.flatten() == 1 X = data.iloc[:,:-1] passed = plt.scatter(X[mask][0], X[mask][1]) failed = plt.scatter(X[~mask][0], X[~mask][1]) plt.contour(u,v,z,0) plt.xlabel('Microchip Test1') plt.ylabel('Microchip Test2') plt.legend((passed, failed), ('Passed', 'Failed')) plt.savefig('fig_2.2.2.png') # Save an image file plt.show() |
data
ex1data1.txt
| 6.1101,17.592 5.5277,9.1302 8.5186,13.662 7.0032,11.854 5.8598,6.8233 8.3829,11.886 7.4764,4.3483 8.5781,12 6.4862,6.5987 5.0546,3.8166 5.7107,3.2522 14.164,15.505 5.734,3.1551 8.4084,7.2258 5.6407,0.71618 5.3794,3.5129 6.3654,5.3048 5.1301,0.56077 6.4296,3.6518 7.0708,5.3893 6.1891,3.1386 20.27,21.767 5.4901,4.263 6.3261,5.1875 5.5649,3.0825 18.945,22.638 12.828,13.501 10.957,7.0467 13.176,14.692 22.203,24.147 5.2524,-1.22 6.5894,5.9966 9.2482,12.134 5.8918,1.8495 8.2111,6.5426 7.9334,4.5623 8.0959,4.1164 5.6063,3.3928 12.836,10.117 6.3534,5.4974 5.4069,0.55657 6.8825,3.9115 11.708,5.3854 5.7737,2.4406 7.8247,6.7318 7.0931,1.0463 5.0702,5.1337 5.8014,1.844 11.7,8.0043 5.5416,1.0179 7.5402,6.7504 5.3077,1.8396 7.4239,4.2885 7.6031,4.9981 6.3328,1.4233 6.3589,-1.4211 6.2742,2.4756 5.6397,4.6042 9.3102,3.9624 9.4536,5.4141 8.8254,5.1694 5.1793,-0.74279 21.279,17.929 14.908,12.054 18.959,17.054 7.2182,4.8852 8.2951,5.7442 10.236,7.7754 5.4994,1.0173 20.341,20.992 10.136,6.6799 7.3345,4.0259 6.0062,1.2784 7.2259,3.3411 5.0269,-2.6807 6.5479,0.29678 7.5386,3.8845 5.0365,5.7014 10.274,6.7526 5.1077,2.0576 5.7292,0.47953 5.1884,0.20421 6.3557,0.67861 9.7687,7.5435 6.5159,5.3436 8.5172,4.2415 9.1802,6.7981 6.002,0.92695 5.5204,0.152 5.0594,2.8214 5.7077,1.8451 7.6366,4.2959 5.8707,7.2029 5.3054,1.9869 8.2934,0.14454 13.394,9.0551 5.4369,0.61705 |
ex1data2.txt
| 2104,3,399900 1600,3,329900 2400,3,369000 1416,2,232000 3000,4,539900 1985,4,299900 1534,3,314900 1427,3,198999 1380,3,212000 1494,3,242500 1940,4,239999 2000,3,347000 1890,3,329999 4478,5,699900 1268,3,259900 2300,4,449900 1320,2,299900 1236,3,199900 2609,4,499998 3031,4,599000 1767,3,252900 1888,2,255000 1604,3,242900 1962,4,259900 3890,3,573900 1100,3,249900 1458,3,464500 2526,3,469000 2200,3,475000 2637,3,299900 1839,2,349900 1000,1,169900 2040,4,314900 3137,3,579900 1811,4,285900 1437,3,249900 1239,3,229900 2132,4,345000 4215,4,549000 2162,4,287000 1664,2,368500 2238,3,329900 2567,4,314000 1200,3,299000 852,2,179900 1852,4,299900 1203,3,239500 |
ex2data1.txt
| 34.62365962451697,78.0246928153624,0 30.28671076822607,43.89499752400101,0 35.84740876993872,72.90219802708364,0 60.18259938620976,86.30855209546826,1 79.0327360507101,75.3443764369103,1 45.08327747668339,56.3163717815305,0 61.10666453684766,96.51142588489624,1 75.02474556738889,46.55401354116538,1 76.09878670226257,87.42056971926803,1 84.43281996120035,43.53339331072109,1 95.86155507093572,38.22527805795094,0 75.01365838958247,30.60326323428011,0 82.30705337399482,76.48196330235604,1 69.36458875970939,97.71869196188608,1 39.53833914367223,76.03681085115882,0 53.9710521485623,89.20735013750205,1 69.07014406283025,52.74046973016765,1 67.94685547711617,46.67857410673128,0 70.66150955499435,92.92713789364831,1 76.97878372747498,47.57596364975532,1 67.37202754570876,42.83843832029179,0 89.67677575072079,65.79936592745237,1 50.534788289883,48.85581152764205,0 34.21206097786789,44.20952859866288,0 77.9240914545704,68.9723599933059,1 62.27101367004632,69.95445795447587,1 80.1901807509566,44.82162893218353,1 93.114388797442,38.80067033713209,0 61.83020602312595,50.25610789244621,0 38.78580379679423,64.99568095539578,0 61.379289447425,72.80788731317097,1 85.40451939411645,57.05198397627122,1 52.10797973193984,63.12762376881715,0 52.04540476831827,69.43286012045222,1 40.23689373545111,71.16774802184875,0 54.63510555424817,52.21388588061123,0 33.91550010906887,98.86943574220611,0 64.17698887494485,80.90806058670817,1 74.78925295941542,41.57341522824434,0 34.1836400264419,75.2377203360134,0 83.90239366249155,56.30804621605327,1 51.54772026906181,46.85629026349976,0 94.44336776917852,65.56892160559052,1 82.36875375713919,40.61825515970618,0 51.04775177128865,45.82270145776001,0 62.22267576120188,52.06099194836679,0 77.19303492601364,70.45820000180959,1 97.77159928000232,86.7278223300282,1 62.07306379667647,96.76882412413983,1 91.56497449807442,88.69629254546599,1 79.94481794066932,74.16311935043758,1 99.2725269292572,60.99903099844988,1 90.54671411399852,43.39060180650027,1 34.52451385320009,60.39634245837173,0 50.2864961189907,49.80453881323059,0 49.58667721632031,59.80895099453265,0 97.64563396007767,68.86157272420604,1 32.57720016809309,95.59854761387875,0 74.24869136721598,69.82457122657193,1 71.79646205863379,78.45356224515052,1 75.3956114656803,85.75993667331619,1 35.28611281526193,47.02051394723416,0 56.25381749711624,39.26147251058019,0 30.05882244669796,49.59297386723685,0 44.66826172480893,66.45008614558913,0 66.56089447242954,41.09209807936973,0 40.45755098375164,97.53518548909936,1 49.07256321908844,51.88321182073966,0 80.27957401466998,92.11606081344084,1 66.74671856944039,60.99139402740988,1 32.72283304060323,43.30717306430063,0 64.0393204150601,78.03168802018232,1 72.34649422579923,96.22759296761404,1 60.45788573918959,73.09499809758037,1 58.84095621726802,75.85844831279042,1 99.82785779692128,72.36925193383885,1 47.26426910848174,88.47586499559782,1 50.45815980285988,75.80985952982456,1 60.45555629271532,42.50840943572217,0 82.22666157785568,42.71987853716458,0 88.9138964166533,69.80378889835472,1 94.83450672430196,45.69430680250754,1 67.31925746917527,66.58935317747915,1 57.23870631569862,59.51428198012956,1 80.36675600171273,90.96014789746954,1 68.46852178591112,85.59430710452014,1 42.0754545384731,78.84478600148043,0 75.47770200533905,90.42453899753964,1 78.63542434898018,96.64742716885644,1 52.34800398794107,60.76950525602592,0 94.09433112516793,77.15910509073893,1 90.44855097096364,87.50879176484702,1 55.48216114069585,35.57070347228866,0 74.49269241843041,84.84513684930135,1 89.84580670720979,45.35828361091658,1 83.48916274498238,48.38028579728175,1 42.2617008099817,87.10385094025457,1 99.31500880510394,68.77540947206617,1 55.34001756003703,64.9319380069486,1 74.77589300092767,89.52981289513276,1 |
ex2data2.txt
| 0.051267,0.69956,1 -0.092742,0.68494,1 -0.21371,0.69225,1 -0.375,0.50219,1 -0.51325,0.46564,1 -0.52477,0.2098,1 -0.39804,0.034357,1 -0.30588,-0.19225,1 0.016705,-0.40424,1 0.13191,-0.51389,1 0.38537,-0.56506,1 0.52938,-0.5212,1 0.63882,-0.24342,1 0.73675,-0.18494,1 0.54666,0.48757,1 0.322,0.5826,1 0.16647,0.53874,1 -0.046659,0.81652,1 -0.17339,0.69956,1 -0.47869,0.63377,1 -0.60541,0.59722,1 -0.62846,0.33406,1 -0.59389,0.005117,1 -0.42108,-0.27266,1 -0.11578,-0.39693,1 0.20104,-0.60161,1 0.46601,-0.53582,1 0.67339,-0.53582,1 -0.13882,0.54605,1 -0.29435,0.77997,1 -0.26555,0.96272,1 -0.16187,0.8019,1 -0.17339,0.64839,1 -0.28283,0.47295,1 -0.36348,0.31213,1 -0.30012,0.027047,1 -0.23675,-0.21418,1 -0.06394,-0.18494,1 0.062788,-0.16301,1 0.22984,-0.41155,1 0.2932,-0.2288,1 0.48329,-0.18494,1 0.64459,-0.14108,1 0.46025,0.012427,1 0.6273,0.15863,1 0.57546,0.26827,1 0.72523,0.44371,1 0.22408,0.52412,1 0.44297,0.67032,1 0.322,0.69225,1 0.13767,0.57529,1 -0.0063364,0.39985,1 -0.092742,0.55336,1 -0.20795,0.35599,1 -0.20795,0.17325,1 -0.43836,0.21711,1 -0.21947,-0.016813,1 -0.13882,-0.27266,1 0.18376,0.93348,0 0.22408,0.77997,0 0.29896,0.61915,0 0.50634,0.75804,0 0.61578,0.7288,0 0.60426,0.59722,0 0.76555,0.50219,0 0.92684,0.3633,0 0.82316,0.27558,0 0.96141,0.085526,0 0.93836,0.012427,0 0.86348,-0.082602,0 0.89804,-0.20687,0 0.85196,-0.36769,0 0.82892,-0.5212,0 0.79435,-0.55775,0 0.59274,-0.7405,0 0.51786,-0.5943,0 0.46601,-0.41886,0 0.35081,-0.57968,0 0.28744,-0.76974,0 0.085829,-0.75512,0 0.14919,-0.57968,0 -0.13306,-0.4481,0 -0.40956,-0.41155,0 -0.39228,-0.25804,0 -0.74366,-0.25804,0 -0.69758,0.041667,0 -0.75518,0.2902,0 -0.69758,0.68494,0 -0.4038,0.70687,0 -0.38076,0.91886,0 -0.50749,0.90424,0 -0.54781,0.70687,0 0.10311,0.77997,0 0.057028,0.91886,0 -0.10426,0.99196,0 -0.081221,1.1089,0 0.28744,1.087,0 0.39689,0.82383,0 0.63882,0.88962,0 0.82316,0.66301,0 0.67339,0.64108,0 1.0709,0.10015,0 -0.046659,-0.57968,0 -0.23675,-0.63816,0 -0.15035,-0.36769,0 -0.49021,-0.3019,0 -0.46717,-0.13377,0 -0.28859,-0.060673,0 -0.61118,-0.067982,0 -0.66302,-0.21418,0 -0.59965,-0.41886,0 -0.72638,-0.082602,0 -0.83007,0.31213,0 -0.72062,0.53874,0 -0.59389,0.49488,0 -0.48445,0.99927,0 -0.0063364,0.99927,0 0.63265,-0.030612,0 |
After running r scripts above, you'll get these png files on your working directory on your Terminal:
Saturday, July 6, 2019
R: Logistic Regression (OLD)
data.csv
0_runme.txt
1_install_packages.r
2_library.r
3_logi_fun.r
4_logistic_regression.r
| number,age,blood_pressure,lung_capacity,sex,illness,weight 1,22,110,4300,M,1,79 2,23,128,4500,M,1,65 3,24,104,3900,F,0,53 4,25,112,3000,F,0,45 5,27,108,4800,M,0,80 6,28,126,3800,F,0,50 7,28,126,3800,F,1,43 8,29,104,4000,F,1,55 9,30,125,3600,F,1,47 10,31,120,3400,F,1,49 11,32,116,3600,M,1,64 12,32,124,3900,M,0,61 13,33,106,3100,F,0,48 14,33,134,2900,F,0,41 15,34,128,4100,M,1,70 16,36,128,3420,M,1,55 17,37,116,3800,M,1,70 18,37,132,4150,M,1,90 19,38,134,2700,F,0,39 20,39,116,4550,M,1,86 21,40,120,2900,F,1,50 22,42,130,3950,F,1,65 23,46,126,3100,M,0,58 24,49,140,3000,F,0,45 25,50,156,3400,M,1,60 26,53,124,3400,M,1,71 27,56,118,3470,M,1,62 28,58,144,2800,M,0,51 29,64,142,2500,F,1,40 30,65,144,2350,F,0,42 |
0_runme.txt
########## R: Logistic Regression ##### Run this script on your R Console ##### Background # # We use machine learning models to learn training data. # The trained machine learning models are expected to predict in a reliable manner even when using new data (which is different from the training data above). # If the machined learning model is over-fitting the training data (including noises and outlier), # the model's prediction accuracy for new data could be lowered. # This is because the model learn noises, outliers, and other meaningful data points of the training data, and regard the entire data as meaningful. # To explain noises and outliers, the model is overly optimized. # # Reasons for over-fitting are mainly (1) numbers of data points are too small, (2) too many explanatory variables, and (3) too big parameters (coefficients). # # To avoid over-fitting, we can use regularization. This method is widely used in various machine learning models. # # Regularization: A way to find a model while avoiding over-fitting # L1 (Lasso): A penalty term is sum of absolute parameter values of the model # By setting weight = 0 of certain data, deleting unnecessary data. # "Dimension comperession to delete unnecessary explanatory variables" # L2 (Ridge): A penalty term is sum of squared parameter values of the model. # This is to have a smoother model. # "More accurate prediction while avoiding over-fitting" # Under both L1 regularization and L2 regularization, # models with lower dimensions have smaller penalty. # If training data have exceptional data such as noises and outliers, # models have to increase its dimensions to explain data including such exceptional data # while trying not to be penalized for increased dimensions. # (Both L1 and L2 can be simultaneously used as liner sum. This is elastic net regularization.) # # # Regression: # A certain objective variable Y is predicted by using weighted explanatory variables X {x0, x1, x2, ..., xn} # Predicted Y = hθ(X) = θ0 * x0 + θ1 * x1 + ... + θn * xn =θT X # # Logistic regression: # Generally, hθ(X) above is a continuous value without any upper and lower boundaries. # To make 0 ≤ hθ(X) ≤ 1, # Logistic Function (AKA Sigmoid Function) g(z) = 1/(1 + e^(−z)) # When doing logistic regressions, # hθ(X) = 1/(1 + e^(−θT X)) # # hθ(x)≥0.5, then Y = 1 # hθ(x)<0.5, then Y = 0 # Set your working directory on your R Console ##### The following directory is dummy - set to your own directory where you save all the r files below. setwd('/Users/XXX/Downloads/') #source('1_install_packages.r') # You have to run this r script only for the first time. #source('2_library.r') source('3_logi_fun.r') source('4_logistic_regression.r') |
Source: https://qiita.com/katsu1110/items/e4ef613559f02f183af5
1_install_packages.r
| ########## install packages #install.packages("glmnet") #install.packages('glmnet_2.0-18.tgz') #zip file dowloaded from https://cran.r-project.org/web/packages/glmnet/index.html |
| ########## library setting #library('glmnet') |
3_logi_fun.r
| logi_fun <- function(data,file,disease){ ans <- glm(data$Y~.,data=data,family=binomial) # family=binomial for logistics regression s.ans <- summary(ans) coe <- s.ans$coefficient RR <- exp(coe[,1]) RRlow <- exp(coe[,1]-1.96*coe[,2]) RRup <- exp(coe[,1]+1.96*coe[,2]) N <- nrow(data) aic <- AIC(ans) result <- cbind(coe,RR,RRlow,RRup,aic,N) colnames(result)[6:7] <- c("RR95%CI.low","RR95%CI.up") if(nrow(result)>=2){ result[2:nrow(result),8:9] <- "" } write.table(disease,file,append=T,quote=F,sep=",",row.names=F,col.names=F) write.table(matrix(c("",colnames(result)),nrow=1),file,append=T,quote=F,sep=",",row.names=F,col.names=F) write.table(result,file,append=T,quote=F,sep=",",row.names=T,col.names=F) write.table("",file,append=T,quote=F,sep=",",row.names=F,col.names=F) } |
4_logistic_regression.r
| df <- read.csv("data.csv",header=T,row.names=1) dat <- df[,c(5,1,2,6)] # 5th column (illness): explanined (target) variable # 1(age),2(blood_pressure),6(weight): explanatory variables colnames(dat)[1] <- "Y" logi_fun(dat,"results_logistic_reg.csv","illness") # See this csv file. # If significance level = 0.05, then only "age" has Pr (p-value) which is less than 0.05 (0.038665). |
results_logistic_reg.csv
| illness ,Estimate,Std. Error,z value,Pr(>|z|),RR,RR95%CI.low,RR95%CI.up,aic,N (Intercept),-6.27037164366909,5.6269544356187,-1.11434555147231,0.265130972267466,0.00189152547909671,3.06938865463388e-08,116.566164818212,42.6982377386664,30 age,0.00171984691269398,0.0447696844915921,0.0384154351817462,0.969356454570465,1.00172132669761,0.91756786481243,1.09359280641977,, blood_pressure,0.016973167573557,0.0445691192249947,0.380827978400756,0.703330897109487,1.01711803021436,0.932037428183773,1.10996517532894,, weight,0.0801901371302698,0.0387817328646643,2.06772960378298,0.038665456531477,1.08349306035207,1.004186680477,1.16906271976586,, |
Subscribe to:
Comments (Atom)
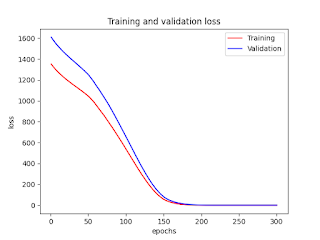
Deep Learning (Regression, Multiple Features/Explanatory Variables, Supervised Learning): Impelementation and Showing Biases and Weights
Deep Learning (Regression, Multiple Features/Explanatory Variables, Supervised Learning): Impelementation and Showing Biases and Weights ...
-
Black-Litterman Portfolio Optimization with Python This is a very basic introduction of the Black-Litterman portfolio optimization with t...
-
This is a great paper to understand having and applying principles to day-to-day business and personal lives. If you do not have your own ...
-
How to win friends & influence people: Part 1 (Influence people and let them move.) Principle 1: Don't criticize, condemn, or ...











