| # Install on Terminal of MacOS #pip3 install -U pandas #pip3 install -U numpy #pip3 install -U matplotlib #pip3 install -U scikit-learn #pip3 install -U seaborn |
1_MacOS_Terminal.txt
| ########## Run Terminal on MacOS and execute ### TO UPDATE cd "YOUR_WORKING_DIRECTORY" #Two numerical arguments after this script name are arbitrary. #2 and 3 in this case mean that the third (x1 = 2) and the fourth (x2 = 3) columns of User_Data.csv will be used for this logistics regression to predict y_pred; y_pred (0 or 1) will be compared with actual results y (0 or 1). python3 lgrs02.py 2 3 4 User_Data.csv |
Data files
User_Data.csv
| User ID,Gender,Age,EstimatedSalary,Purchased 15624510,Male,19,19000,0 15810944,Male,35,20000,0 15668575,Female,26,43000,0 15603246,Female,27,57000,0 15804002,Male,19,76000,0 15728773,Male,27,58000,0 15598044,Female,27,84000,0 15694829,Female,32,150000,1 15600575,Male,25,33000,0 15727311,Female,35,65000,0 15570769,Female,26,80000,0 15606274,Female,26,52000,0 15746139,Male,20,86000,0 15704987,Male,32,18000,0 15628972,Male,18,82000,0 15697686,Male,29,80000,0 15733883,Male,47,25000,1 15617482,Male,45,26000,1 15704583,Male,46,28000,1 15621083,Female,48,29000,1 15649487,Male,45,22000,1 15736760,Female,47,49000,1 15714658,Male,48,41000,1 15599081,Female,45,22000,1 15705113,Male,46,23000,1 15631159,Male,47,20000,1 15792818,Male,49,28000,1 15633531,Female,47,30000,1 15744529,Male,29,43000,0 15669656,Male,31,18000,0 15581198,Male,31,74000,0 15729054,Female,27,137000,1 15573452,Female,21,16000,0 15776733,Female,28,44000,0 15724858,Male,27,90000,0 15713144,Male,35,27000,0 15690188,Female,33,28000,0 15689425,Male,30,49000,0 15671766,Female,26,72000,0 15782806,Female,27,31000,0 15764419,Female,27,17000,0 15591915,Female,33,51000,0 15772798,Male,35,108000,0 15792008,Male,30,15000,0 15715541,Female,28,84000,0 15639277,Male,23,20000,0 15798850,Male,25,79000,0 15776348,Female,27,54000,0 15727696,Male,30,135000,1 15793813,Female,31,89000,0 15694395,Female,24,32000,0 15764195,Female,18,44000,0 15744919,Female,29,83000,0 15671655,Female,35,23000,0 15654901,Female,27,58000,0 15649136,Female,24,55000,0 15775562,Female,23,48000,0 15807481,Male,28,79000,0 15642885,Male,22,18000,0 15789109,Female,32,117000,0 15814004,Male,27,20000,0 15673619,Male,25,87000,0 15595135,Female,23,66000,0 15583681,Male,32,120000,1 15605000,Female,59,83000,0 15718071,Male,24,58000,0 15679760,Male,24,19000,0 15654574,Female,23,82000,0 15577178,Female,22,63000,0 15595324,Female,31,68000,0 15756932,Male,25,80000,0 15726358,Female,24,27000,0 15595228,Female,20,23000,0 15782530,Female,33,113000,0 15592877,Male,32,18000,0 15651983,Male,34,112000,1 15746737,Male,18,52000,0 15774179,Female,22,27000,0 15667265,Female,28,87000,0 15655123,Female,26,17000,0 15595917,Male,30,80000,0 15668385,Male,39,42000,0 15709476,Male,20,49000,0 15711218,Male,35,88000,0 15798659,Female,30,62000,0 15663939,Female,31,118000,1 15694946,Male,24,55000,0 15631912,Female,28,85000,0 15768816,Male,26,81000,0 15682268,Male,35,50000,0 15684801,Male,22,81000,0 15636428,Female,30,116000,0 15809823,Male,26,15000,0 15699284,Female,29,28000,0 15786993,Female,29,83000,0 15709441,Female,35,44000,0 15710257,Female,35,25000,0 15582492,Male,28,123000,1 15575694,Male,35,73000,0 15756820,Female,28,37000,0 15766289,Male,27,88000,0 15593014,Male,28,59000,0 15584545,Female,32,86000,0 15675949,Female,33,149000,1 15672091,Female,19,21000,0 15801658,Male,21,72000,0 15706185,Female,26,35000,0 15789863,Male,27,89000,0 15720943,Male,26,86000,0 15697997,Female,38,80000,0 15665416,Female,39,71000,0 15660200,Female,37,71000,0 15619653,Male,38,61000,0 15773447,Male,37,55000,0 15739160,Male,42,80000,0 15689237,Male,40,57000,0 15679297,Male,35,75000,0 15591433,Male,36,52000,0 15642725,Male,40,59000,0 15701962,Male,41,59000,0 15811613,Female,36,75000,0 15741049,Male,37,72000,0 15724423,Female,40,75000,0 15574305,Male,35,53000,0 15678168,Female,41,51000,0 15697020,Female,39,61000,0 15610801,Male,42,65000,0 15745232,Male,26,32000,0 15722758,Male,30,17000,0 15792102,Female,26,84000,0 15675185,Male,31,58000,0 15801247,Male,33,31000,0 15725660,Male,30,87000,0 15638963,Female,21,68000,0 15800061,Female,28,55000,0 15578006,Male,23,63000,0 15668504,Female,20,82000,0 15687491,Male,30,107000,1 15610403,Female,28,59000,0 15741094,Male,19,25000,0 15807909,Male,19,85000,0 15666141,Female,18,68000,0 15617134,Male,35,59000,0 15783029,Male,30,89000,0 15622833,Female,34,25000,0 15746422,Female,24,89000,0 15750839,Female,27,96000,1 15749130,Female,41,30000,0 15779862,Male,29,61000,0 15767871,Male,20,74000,0 15679651,Female,26,15000,0 15576219,Male,41,45000,0 15699247,Male,31,76000,0 15619087,Female,36,50000,0 15605327,Male,40,47000,0 15610140,Female,31,15000,0 15791174,Male,46,59000,0 15602373,Male,29,75000,0 15762605,Male,26,30000,0 15598840,Female,32,135000,1 15744279,Male,32,100000,1 15670619,Male,25,90000,0 15599533,Female,37,33000,0 15757837,Male,35,38000,0 15697574,Female,33,69000,0 15578738,Female,18,86000,0 15762228,Female,22,55000,0 15614827,Female,35,71000,0 15789815,Male,29,148000,1 15579781,Female,29,47000,0 15587013,Male,21,88000,0 15570932,Male,34,115000,0 15794661,Female,26,118000,0 15581654,Female,34,43000,0 15644296,Female,34,72000,0 15614420,Female,23,28000,0 15609653,Female,35,47000,0 15594577,Male,25,22000,0 15584114,Male,24,23000,0 15673367,Female,31,34000,0 15685576,Male,26,16000,0 15774727,Female,31,71000,0 15694288,Female,32,117000,1 15603319,Male,33,43000,0 15759066,Female,33,60000,0 15814816,Male,31,66000,0 15724402,Female,20,82000,0 15571059,Female,33,41000,0 15674206,Male,35,72000,0 15715160,Male,28,32000,0 15730448,Male,24,84000,0 15662067,Female,19,26000,0 15779581,Male,29,43000,0 15662901,Male,19,70000,0 15689751,Male,28,89000,0 15667742,Male,34,43000,0 15738448,Female,30,79000,0 15680243,Female,20,36000,0 15745083,Male,26,80000,0 15708228,Male,35,22000,0 15628523,Male,35,39000,0 15708196,Male,49,74000,0 15735549,Female,39,134000,1 15809347,Female,41,71000,0 15660866,Female,58,101000,1 15766609,Female,47,47000,0 15654230,Female,55,130000,1 15794566,Female,52,114000,0 15800890,Female,40,142000,1 15697424,Female,46,22000,0 15724536,Female,48,96000,1 15735878,Male,52,150000,1 15707596,Female,59,42000,0 15657163,Male,35,58000,0 15622478,Male,47,43000,0 15779529,Female,60,108000,1 15636023,Male,49,65000,0 15582066,Male,40,78000,0 15666675,Female,46,96000,0 15732987,Male,59,143000,1 15789432,Female,41,80000,0 15663161,Male,35,91000,1 15694879,Male,37,144000,1 15593715,Male,60,102000,1 15575002,Female,35,60000,0 15622171,Male,37,53000,0 15795224,Female,36,126000,1 15685346,Male,56,133000,1 15691808,Female,40,72000,0 15721007,Female,42,80000,1 15794253,Female,35,147000,1 15694453,Male,39,42000,0 15813113,Male,40,107000,1 15614187,Male,49,86000,1 15619407,Female,38,112000,0 15646227,Male,46,79000,1 15660541,Male,40,57000,0 15753874,Female,37,80000,0 15617877,Female,46,82000,0 15772073,Female,53,143000,1 15701537,Male,42,149000,1 15736228,Male,38,59000,0 15780572,Female,50,88000,1 15769596,Female,56,104000,1 15586996,Female,41,72000,0 15722061,Female,51,146000,1 15638003,Female,35,50000,0 15775590,Female,57,122000,1 15730688,Male,41,52000,0 15753102,Female,35,97000,1 15810075,Female,44,39000,0 15723373,Male,37,52000,0 15795298,Female,48,134000,1 15584320,Female,37,146000,1 15724161,Female,50,44000,0 15750056,Female,52,90000,1 15609637,Female,41,72000,0 15794493,Male,40,57000,0 15569641,Female,58,95000,1 15815236,Female,45,131000,1 15811177,Female,35,77000,0 15680587,Male,36,144000,1 15672821,Female,55,125000,1 15767681,Female,35,72000,0 15600379,Male,48,90000,1 15801336,Female,42,108000,1 15721592,Male,40,75000,0 15581282,Male,37,74000,0 15746203,Female,47,144000,1 15583137,Male,40,61000,0 15680752,Female,43,133000,0 15688172,Female,59,76000,1 15791373,Male,60,42000,1 15589449,Male,39,106000,1 15692819,Female,57,26000,1 15727467,Male,57,74000,1 15734312,Male,38,71000,0 15764604,Male,49,88000,1 15613014,Female,52,38000,1 15759684,Female,50,36000,1 15609669,Female,59,88000,1 15685536,Male,35,61000,0 15750447,Male,37,70000,1 15663249,Female,52,21000,1 15638646,Male,48,141000,0 15734161,Female,37,93000,1 15631070,Female,37,62000,0 15761950,Female,48,138000,1 15649668,Male,41,79000,0 15713912,Female,37,78000,1 15586757,Male,39,134000,1 15596522,Male,49,89000,1 15625395,Male,55,39000,1 15760570,Male,37,77000,0 15566689,Female,35,57000,0 15725794,Female,36,63000,0 15673539,Male,42,73000,1 15705298,Female,43,112000,1 15675791,Male,45,79000,0 15747043,Male,46,117000,1 15736397,Female,58,38000,1 15678201,Male,48,74000,1 15720745,Female,37,137000,1 15637593,Male,37,79000,1 15598070,Female,40,60000,0 15787550,Male,42,54000,0 15603942,Female,51,134000,0 15733973,Female,47,113000,1 15596761,Male,36,125000,1 15652400,Female,38,50000,0 15717893,Female,42,70000,0 15622585,Male,39,96000,1 15733964,Female,38,50000,0 15753861,Female,49,141000,1 15747097,Female,39,79000,0 15594762,Female,39,75000,1 15667417,Female,54,104000,1 15684861,Male,35,55000,0 15742204,Male,45,32000,1 15623502,Male,36,60000,0 15774872,Female,52,138000,1 15611191,Female,53,82000,1 15674331,Male,41,52000,0 15619465,Female,48,30000,1 15575247,Female,48,131000,1 15695679,Female,41,60000,0 15713463,Male,41,72000,0 15785170,Female,42,75000,0 15796351,Male,36,118000,1 15639576,Female,47,107000,1 15693264,Male,38,51000,0 15589715,Female,48,119000,1 15769902,Male,42,65000,0 15587177,Male,40,65000,0 15814553,Male,57,60000,1 15601550,Female,36,54000,0 15664907,Male,58,144000,1 15612465,Male,35,79000,0 15810800,Female,38,55000,0 15665760,Male,39,122000,1 15588080,Female,53,104000,1 15776844,Male,35,75000,0 15717560,Female,38,65000,0 15629739,Female,47,51000,1 15729908,Male,47,105000,1 15716781,Female,41,63000,0 15646936,Male,53,72000,1 15768151,Female,54,108000,1 15579212,Male,39,77000,0 15721835,Male,38,61000,0 15800515,Female,38,113000,1 15591279,Male,37,75000,0 15587419,Female,42,90000,1 15750335,Female,37,57000,0 15699619,Male,36,99000,1 15606472,Male,60,34000,1 15778368,Male,54,70000,1 15671387,Female,41,72000,0 15573926,Male,40,71000,1 15709183,Male,42,54000,0 15577514,Male,43,129000,1 15778830,Female,53,34000,1 15768072,Female,47,50000,1 15768293,Female,42,79000,0 15654456,Male,42,104000,1 15807525,Female,59,29000,1 15574372,Female,58,47000,1 15671249,Male,46,88000,1 15779744,Male,38,71000,0 15624755,Female,54,26000,1 15611430,Female,60,46000,1 15774744,Male,60,83000,1 15629885,Female,39,73000,0 15708791,Male,59,130000,1 15793890,Female,37,80000,0 15646091,Female,46,32000,1 15596984,Female,46,74000,0 15800215,Female,42,53000,0 15577806,Male,41,87000,1 15749381,Female,58,23000,1 15683758,Male,42,64000,0 15670615,Male,48,33000,1 15715622,Female,44,139000,1 15707634,Male,49,28000,1 15806901,Female,57,33000,1 15775335,Male,56,60000,1 15724150,Female,49,39000,1 15627220,Male,39,71000,0 15672330,Male,47,34000,1 15668521,Female,48,35000,1 15807837,Male,48,33000,1 15592570,Male,47,23000,1 15748589,Female,45,45000,1 15635893,Male,60,42000,1 15757632,Female,39,59000,0 15691863,Female,46,41000,1 15706071,Male,51,23000,1 15654296,Female,50,20000,1 15755018,Male,36,33000,0 15594041,Female,49,36000,1 |
Python files
| #################### Logistic Regression in Python (x1, x2: Two Independent Variables, y: One Dependent Variable, and various metrics) #################### ##### Data # # Download csv data from the following website and save it to your working directory (where this lgrs01.py script is saved): # https://drive.google.com/open?id=1Upqoz2gIAYq6LByD7YjHU-9_9K4EOhOh # User_Data.csv # #User Database – This dataset contains information of users from a companies database. It contains information about UserID, Gender, Age, EstimatedSalary, Purchased. We are using this dataset for predicting that a user will purchase the company’s newly launched product or not. ##### Run this script on Terminal of MacOs as follows: # #python3 lgrs01.py 2 3 4 User_Data.csv # Three numerical arguments after this script name are arbitrary. # 2 and 3 in this case mean that the third (nx1 = 2) and the fourth (nx2 = 3) columns of User_Data.csv will be used for this logistics regression to predict y_pred. # y_pred will be compared with actual results y (ny = 4 in this case). # # Generally, this is described as follows. #python3 lgrs01.py (nx1) (nx2) (ny) (dt: dataset) #Reference: #ML | Logistic Regression using Python #https://www.geeksforgeeks.org/ml-logistic-regression-using-python/ import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns import sys ### columns of User_Data.csv #Two numerical arguments (x1 and x2) after this script name (lgrs01.py) are arbitrary. #2 and 3 in this case mean that the third (x1 = 2) and the fourth (x2 = 3) columns of User_Data.csv will be used for this logistics regression to predict y_pred; y_pred (0 or 1) will be compared with actual results y (0 or 1). nx1 = int(sys.argv[1]) nx2 = int(sys.argv[2]) ny = int(sys.argv[3]) dt = str(sys.argv[4]) # Loading dataset – User_Data #dataset = pd.read_csv('User_Data.csv') dataset = pd.read_csv(dt) #print(dataset) ''' User ID Gender Age EstimatedSalary Purchased 0 15624510 Male 19 19000 0 1 15810944 Male 35 20000 0 2 15668575 Female 26 43000 0 3 15603246 Female 27 57000 0 4 15804002 Male 19 76000 0 .. ... ... ... ... ... 395 15691863 Female 46 41000 1 396 15706071 Male 51 23000 1 397 15654296 Female 50 20000 1 398 15755018 Male 36 33000 0 399 15594041 Female 49 36000 1 [400 rows x 5 columns] ''' #Now, to predict whether a user will purchase the product or not, one needs to find out the relationship between Age and Estimated Salary. Here User ID and Gender are not important factors for finding out this. # input #x = dataset.iloc[:, [2, 3]].values x = dataset.iloc[:, [nx1, nx2]].values # ignore the following # 0: User ID, # 1: Gender, # and use the following # 2: Age (to be used as x1), # 3: EstimatedSalary (to be used as x2), #print(x) ''' [[ 19 19000] [ 35 20000] (omitted) [ 49 36000]] ''' # output #y = dataset.iloc[:, 4].values y = dataset.iloc[:, ny].values # This shows the results whether or not a user purchased. # 4: Purchased (to be used as y) #print(y) ''' [0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 0 1 0 0 0 1 0 1 1 1 0 0 1 1 0 1 1 0 1 1 0 1 0 0 0 1 1 0 1 1 0 1 0 1 0 1 0 0 1 1 0 1 0 0 1 1 0 1 1 0 1 1 0 0 1 0 0 1 1 1 1 1 0 1 1 1 1 0 1 1 0 1 0 1 0 1 1 1 1 0 0 0 1 1 0 1 1 1 1 1 0 0 0 1 1 0 0 1 0 1 0 1 1 0 1 0 1 1 0 1 1 0 0 0 1 1 0 1 0 0 1 0 1 0 0 1 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 1 1 0 1 0 1 1 1 0 1 1 1 1 0 1 1 1 0 1 0 1 0 0 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 0 1] ''' # Splitting the dataset to train and test. # 75% of data is used for training the model and 25% of it is used to test the performance of our model. #from sklearn.cross_validation import train_test_split #changed to the following new module from sklearn.model_selection import train_test_split xtrain, xtest, ytrain, ytest = train_test_split(x, y, test_size = 0.25, random_state = 0) # saving raw data xtrain_raw = xtrain xtest_raw = xtest ytrain_raw = ytrain ytest_raw = ytest # raw Training Data and Test Data output pd.DataFrame(data=xtrain_raw).to_csv("xtrain_raw.csv", header=False, index=False) pd.DataFrame(data=xtest_raw).to_csv("xtest_raw.csv", header=False, index=False) pd.DataFrame(data=ytrain_raw).to_csv("ytrain_raw.csv", header=False, index=False) pd.DataFrame(data=ytest_raw).to_csv("ytest_raw.csv", header=False, index=False) # Training Data trainx1mean = xtrain_raw[:,0].mean() trainx2mean = xtrain_raw[:,1].mean() trainx1std = xtrain_raw[:,0].std() trainx2std = xtrain_raw[:,1].std() # Training Data testx1mean = xtest_raw[:,0].mean() testx2mean = xtest_raw[:,1].mean() testx1std = xtest_raw[:,0].std() testx2std = xtest_raw[:,1].std() # Standardization #Now, it is very important to perform feature scaling here because Age and Estimated Salary values lie in different ranges. If we don’t scale the features then Estimated Salary feature will dominate Age feature when the model finds the nearest neighbor to a data point in data space. from sklearn.preprocessing import StandardScaler sc_x = StandardScaler() xtrain = sc_x.fit_transform(xtrain) # standardization model building and calculating standardized training data (xtrain) #print(xtrain) #print(len(xtrain)) #300 xtest = sc_x.transform(xtest) # NO standarization model building, only calculating standardized test data (xtest) #print(xtest) #100 #print(len(xtest)) #print (xtrain[0:10, :]) ''' [[ 0.58164944 -0.88670699] [-0.60673761 1.46173768] [-0.01254409 -0.5677824 ] [-0.60673761 1.89663484] [ 1.37390747 -1.40858358] [ 1.47293972 0.99784738] [ 0.08648817 -0.79972756] [-0.01254409 -0.24885782] [-0.21060859 -0.5677824 ] [-0.21060859 -0.19087153]] ''' #Here once see that Age and Estimated salary features values are sacled and now there in the -1 to 1. Hence, each feature will contribute equally in decision making i.e., finalizing the hypothesis. #Finally, we are training our Logistic Regression model. from sklearn.linear_model import LogisticRegression classifier = LogisticRegression(random_state = 0) classifier.fit(xtrain, ytrain) #After training the model, it time to use it to do prediction on testing data. y_pred = classifier.predict(xtest) # Confusion Matrix # Let’s test the performance of our model. from sklearn.metrics import confusion_matrix cm = confusion_matrix(ytest, y_pred) #print ("Confusion Matrix : \n", cm) ''' Confusion Matrix : [[65 3] [ 8 24]] ''' ''' Out of 100 : TruePostive + TrueNegative = 24 + 65 FalsePositive + FalseNegative = 3 + 8 [[TrueNegative(TN) FalsePositive(FP)] [ FalseNegative(FN) TruePositive(TP)]] Predicted Labels: Negative Positive Actual Results: Negative TrueNegative(TN) FalsePositive(FP) Positive FalseNegative(FN) TruePositive(TP) ''' #sklearn.metrics # # # 1. Accuracy # = (TruePostive + TrueNegative)/(All Dataset) # = (TruePostive + TrueNegative)/(TruePostive + TrueNegative + FalsePositive + FalseNegative) # = (TP + TN)/(TP + TN + FP + FN) # = (24 + 65)/(24 + 65 + 3 + 8) # = 0.89 from sklearn.metrics import accuracy_score print ("Accuracy : ", accuracy_score(ytest, y_pred)) #Accuracy : 0.89 # # # 2. Precision # = (TruePostive)/(TruePostive + FalsePositive) # = (TP)/(TP + FP) # = (24)/(24 + 3) # = 0.888888888888889 from sklearn.metrics import precision_score print ("Precision : ", precision_score(ytest, y_pred)) #Precision : 0.8888888888888888 # # #3. Recall # = (TruePostive)/(TruePostive + FalseNegative) # = (TP)/(TP + FN) # = (24)/(24 + 8) # = 0.75 from sklearn.metrics import recall_score print ("Recall : ", recall_score(ytest, y_pred)) #Recall : 0.75 # # #4. F1-measure # = (2 * Precision * Recall)/(Precision + Recall) # = (2 * TruePostive)/(2 * TruePostive + FalsePositive + FalseNegative) # = (2 * TP)/(2 * TP + FP + FN) # = (2 * 24)/(2 * 24 + 3 + 8) # = 0.813559322033898 from sklearn.metrics import f1_score print ("F1-measure : ", f1_score(ytest, y_pred)) #F1-measure : 0.8135593220338982 ##### Visualization (Standardized Test set) # Visualizing the performance of our model. from matplotlib.colors import ListedColormap ### Standardized Test Data set X_set, y_set = xtest, ytest pd.DataFrame(data=xtest).to_csv("xtest.csv", header=False, index=False) pd.DataFrame(data=ytest).to_csv("ytest.csv", header=False, index=False) X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01), np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01)) #size of Figure 1 plt.figure(figsize=(9, 9)) #This is the line applying the classifier on all the pixel observation points. #It colors all the red pixel points and the green pixel points. #contour function make the contour between red and green regions. plt.contourf(X1, X2, classifier.predict( np.array([X1.ravel(), X2.ravel()]).T).reshape( X1.shape), alpha = 0.75, cmap = ListedColormap(('red', 'green'))) plt.xlim(X1.min(), X1.max()) plt.ylim(X2.min(), X2.max()) for i, j in enumerate(np.unique(y_set)): plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], c = ListedColormap(('yellow', 'blue'))(i), label = str(j) + " (Test Data)") ##### Visualization (Standardized Training set) ### Standardized Training Data set X_set, y_set = xtrain, ytrain for i, j in enumerate(np.unique(y_set)): plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], c = ListedColormap(('red', 'green'))(i), label = str(j) + " (Training Data)") ##### Figure 1: Logistic Regression plt.title('Logistic Regession (Scatter Plot: Training Data and Test Data)') plt.xlabel('x1 (Standardized)') plt.ylabel('x2 (Standardized)') plt.legend() plt.text(-2.0, -2.0, 'Training Data: x1 mean = ' + str(round(trainx1mean, 2)) + ', x1 std = ' + str(round(trainx1std, 2)),fontsize=10) plt.text(-2.0, -2.2, ' Test Data: x1 mean = ' + str(round(testx1mean, 2)) + ', x1 std = ' + str(round(testx1std, 2)),fontsize=10) plt.text(-2.9, -2.5, 'Note: The model built by Standardized Training Data is used to fill both green region (1) and red region (0).',fontsize=10) plt.text(-2.9, 3.0, 'Training Data: x2 mean = ' + str(round(trainx2mean, 2)) + ', x2 std = ' + str(round(trainx2std, 2)),fontsize=10) plt.text(-2.9, 2.7, ' Test Data: x2 mean = ' + str(round(testx2mean, 2)) + ', x2 std = ' + str(round(testx2std, 2)),fontsize=10) plt.savefig("Figure_1_Logistic_Regression_Standardized_Training_and_Test_Data.png") # added to save a figure plt.show() #Analysing the performance measures – accuracy and confusion matrix and the graph, we can clearly say that our model is performing really good. ##### Figure 2: Confusion Matrix #print ("Confusion Matrix : \n", cm) ''' Confusion Matrix : [[65 3] [ 8 24]] ''' ''' Out of 100 : TruePostive + TrueNegative = 24 + 65 FalsePositive + FalseNegative = 3 + 8 [[TrueNegative(TN) FalsePositive(FP)] [ FalseNegative(FN) TruePositive(TP)]] Predicted Labels: Negative Positive Actual Results: Negative TrueNegative(TN) FalsePositive(FP) Positive FalseNegative(FN) TruePositive(TP) ''' #use 1, 2 as there are two independent variables x1 and x2 class_names=[1,2] #fig, ax = plt.subplots() fig, ax = plt.subplots(figsize=(6,5)) tick_marks = np.arange(len(class_names)) plt.xticks(tick_marks, class_names) plt.yticks(tick_marks, class_names) #sns.heatmap(pd.DataFrame(cm), annot=True, cmap="Blues" ,fmt='g') sns.heatmap(pd.DataFrame(cm), annot=True, cmap="coolwarm" ,fmt='g') ax.xaxis.set_label_position("top") #plt.tight_layout() plt.tight_layout(pad=3.00) plt.title('Confusion Matrix (Test Data)') plt.xlabel('Predicted Labels') plt.ylabel('Actual Results') #print("Accuracy:",metrics.accuracy_score(y_test, y_pred)) plt.savefig("Figure_2_Confusion_Matrix_Test_Data.png") plt.show() |
Figures
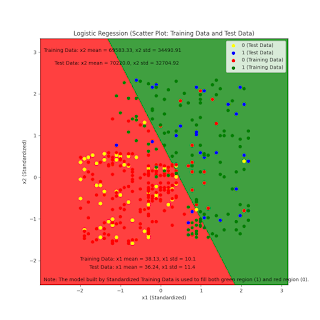
Figure_1_Logistic_Regression_Standardized_Training_and_Test_Data.png
Figure_2_Confusion_Matrix_Test_Data.png
References
https://www.geeksforgeeks.org/ml-logistic-regression-using-python/
Download csv data from the following website and save it to your working directory (where the lgrs01.py script is saved):
https://drive.google.com/open?id=1Upqoz2gIAYq6LByD7YjHU-9_9K4EOhOh
User_Data.csv
https://drive.google.com/open?id=1Upqoz2gIAYq6LByD7YjHU-9_9K4EOhOh
User_Data.csv


No comments:
Post a Comment