The Financial Journal (Global): Multinomial Logistic Regression with L2 (or L1) Regularitation of Standardized Training Data (plus Test Data) in Python

Multinomial Logistic Regression with L2 (or L1) Regularitation of Standardized Training Data (plus Test Data) in Python

**0_MacOS_Python_setup.txt**
# Install on Terminal of MacOS #pip3 install -U scikit-learn #pip3 install -U matplotlib #pip3 install -U numpy #pip3 install -U pandas #pip3 install -U seaborn

1_MacOS_Terminal.txt

########## Run Terminal on MacOS and execute
### TO UPDATE
cd "YOUR_WORKING_DIRECTORY"

python3 mlgstcreg.py l2 1
#python3 mlgstcreg.py l2 10
#python3 mlgstcreg.py l2 100
#python3 mlgstcreg.py l2 1000

Data files

X.csv

4.494746752403546,2.565907751154284
3.3841445311320393,5.169101554140335
4.641125838188323,0.617920368071555
3.3436279255182804,1.7859485832624662
1.854026499900972,2.580673970131322
2.203708371908368,4.056653316946923
3.076269872380446,2.172074458526128
2.6277174035873467,2.471886759188408
4.11294688851731,1.7098624009494876
2.4427445896156783,0.7921262219144254
-1.6104728221529445,2.9243562822910114
3.2224973962333587,0.9504201626223048
5.20991777250232,-0.05678366166746862
2.064712315761789,1.7352820606362547
4.167677153069308,4.077987100384831
2.2191287508753765,2.5348025640025753
0.7444813552199567,-0.8012692296630051
1.5079779199085814,2.2211108325699005
3.7398937663463703,3.7004218892750256
1.4522371617508665,1.5724793501936696
0.5171221759355953,-0.008208625571572536
-0.4130304446548192,4.758813021080532
1.279242972473774,1.3804693813343385
0.2282798109393096,3.0995374058317706
-0.28239622430120104,1.6991398104583528
0.7336190445083068,2.5471627597885957
1.2776124467202452,0.33033395303991564
1.960144310465579,2.6057527405007535
2.094069558025663,2.427759860020327
1.1029330922034843,1.4870065234299592
1.0489973145957656,1.4915150425552421
0.8500374997394751,-0.4413322687061778
2.2509184566947953,1.4317959509113165
-0.30544861163758075,2.654472942190161
0.7168863479702925,2.073461883237738
3.0310897612296968,2.1824093817074885
3.6113559010583245,0.2536925776873813
2.568997005660739,1.0315322817422565
0.7685068615511554,1.181382953515044
1.5593981836737902,2.079429788716632
0.35222929296732475,3.2739610351955215
2.65854613775456,-0.172576656243288
4.104706436697249,4.681192185498803
3.6670460565823193,1.745547856986421
0.4857271207132452,3.491219933093745
1.4298216935543513,3.728798397790962
2.294545298699255,3.3811761709382586
2.503978192058076,2.999245357265979
2.0148492717085826,4.52560227312357
2.1794808027306107,2.5684988097132244
9.26171268561018,4.665612829739954
3.7994554323686414,8.679044351219694
3.9680906587940683,10.366450644211836
5.283590910349264,5.705370290222793
9.330633289873484,9.564326840121662
9.234707005589334,8.569315382059349
4.508313356701943,10.308329544524192
5.53580454491248,8.389895248377957
7.640688535753728,6.731514643080693
7.063616669319316,8.597308810232208
6.6519881452276515,5.095781972826784
6.5165636704814665,9.29736776350474
4.7969731776409015,6.74082537358526
5.246291939324073,10.203018734320477
7.1644486768077105,7.705744602514913
4.66646624149673,7.934006997257856
4.8320215705383225,7.0551321441644586
4.898682286454355,8.171616834778561
6.998684589554707,6.639215972185542
6.685903746468299,5.106761931080872
3.4170660822610364,7.761048751014304
6.288686962260316,8.099906713100598
10.12772783185664,8.635886458173985
4.4189455272526255,8.934728963864012
3.7207815069376498,6.200512012469322
5.881802072387676,9.967596644675044
4.710046809030184,5.568566461709612
5.829475225561735,5.850821898302097
7.9513906587206815,5.129503758820057
4.012525993931379,6.241673437930561
5.137382491582886,10.342047552043745
7.644445075358459,7.151643198344877
3.8774834199866217,8.46247957515756
4.267576199811119,4.324377974317278
8.05772796125969,7.548960706937425
7.594974269386494,7.552052488674493
7.484074153295792,5.872390595376473
4.2086388506648875,8.180556335824212
4.608453642359058,5.805664750588825
5.210994559408913,7.030274791504974
5.386864560138938,4.618514501867448
4.885220225607101,3.1489527746384947
7.082932639669101,4.22515474383443
4.087151945077339,7.090352567660865
4.719039314852367,9.672579676064801
3.760706145442498,7.462545673918223
5.931960162965485,4.976802713921405
6.906341762455969,6.702873038471027
7.336780447503662,8.426351034909207
9.746834572913645,9.314934314159679

**y.csv**
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0

Python files

mlgstcreg.py

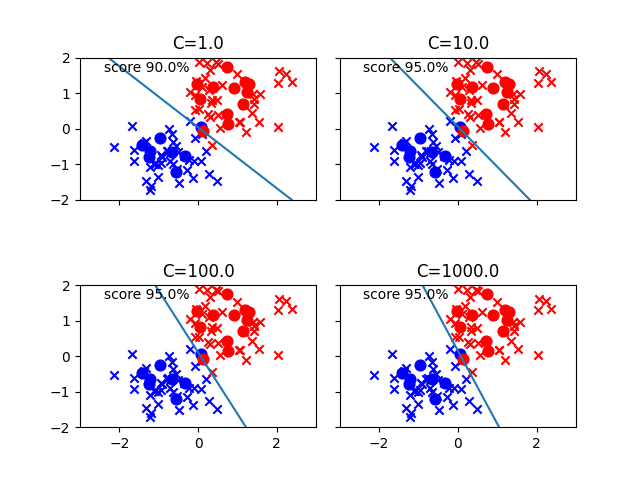
#################### Multinomial Logistic Regression with L2 (or L1) Regularitation of Standardized Training Data (plus Test Data) in Python ####################

#Run this script on Terminal of MacOS as follows:

#python3 mlgstcreg.py l2 1

##python3 mlgstcreg.py (penalty/regularization of LogisticRegression()) (parameter c, 1 by default)

#Reference

#http://ailaby.com/logistic_reg/

##########Overview

'''

We have to avoid overfitting, i.e., letting a model learn outliers and noises of training data too well.

Reasons of overfitting are

(1) variables are too many,

(2) parameters are too big/impactful, and/or

(3) data is not enough.

We can use L1 regularization (e.g., linear Lasso Regression) to eliminate redundant / unnecessary parameters as in (1).

Also, L2 regularization (e.g., linear Ridge Regression) is to avoid (2).

'''

########## import

'''

from sklearn import datasets

import matplotlib.pyplot as plt

import seaborn as sns

'''

#from sklearn.cross_validation import train_test_split

from sklearn.model_selection import train_test_split

from sklearn.preprocessing import StandardScaler

from sklearn.linear_model import LogisticRegression

from sklearn.metrics import confusion_matrix

import matplotlib.pyplot as plt

import numpy as np

import pandas as pd

import seaborn as sns

import sys

import math

########## arguments

pnlty = str(sys.argv[1]) #l2 or l1

c = int(sys.argv[2]) #C = 1 by default. The larger the C, the weaker regularization is going to be.

########## Multinomial Logistic Regression with Regularitation

'''

##### generate dataset with TWO classes as the mixture of training data and test data

np.random.seed(seed=0)

X_0 = np.random.multivariate_normal( [2,2], [[2,0],[0,2]], 50 )

y_0 = np.zeros(len(X_0))

X_1 = np.random.multivariate_normal( [6,7], [[3,0],[0,3]], 50 )

y_1 = np.ones(len(X_1))

X = np.vstack((X_0, X_1))

#print(X)

#print(type(X))

#<class 'numpy.ndarray'>

y = np.append(y_0, y_1)

#print(y)

#print(type(y))

#<class 'numpy.ndarray'>

##### save dataset

pd.DataFrame(data=X).to_csv("X.csv", header=False, index=False)

pd.DataFrame(data=y).to_csv("y.csv", header=False, index=False)

'''

##### load raw dataset

X = pd.read_csv('X.csv', header=None).values

y = pd.read_csv('y.csv', header=None).values.ravel()

#print(type(X))

#<class 'numpy.ndarray'>

#print(type(y))

#<class 'numpy.ndarray'>

##### plot raw data

plt.scatter(X[y==0, 0], X[y==0, 1], c='blue', marker='*', label='raw data 0')

plt.scatter(X[y==1, 0], X[y==1, 1], c='red', marker='*', label='raw data 1')

plt.legend(loc='upper left')

plt.title('Raw Data')

plt.xlabel('X1: Raw Data')

plt.ylabel('X2: Raw Data')

plt.savefig('Figure_1_Raw_Data.png')

plt.show()

plt.close()

##### splitting Training Data and Test Data

#X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=3)

#random_state=3 is to fix results. You can change this number to, say, 1, 2, or any other integer you like.

##### Standardization of Training and Test Data (Average=0, SD=1)

sc = StandardScaler()

X_train_std = sc.fit_transform(X_train)

X_test_std = sc.transform(X_test)

##### max and min of X and y

xmax = max(

max(X_train_std[y_train==0, 0]),

max(X_train_std[y_train==1, 0]),

max(X_test_std[y_test==0, 0]),

max(X_test_std[y_test==1, 0])

)

xmin = min(

min(X_train_std[y_train==0, 0]),

min(X_train_std[y_train==1, 0]),

min(X_test_std[y_test==0, 0]),

min(X_test_std[y_test==1, 0])

)

ymax = max(

max(X_train_std[y_train==0, 1]),

max(X_train_std[y_train==1, 1]),

max(X_test_std[y_test==0, 1]),

max(X_test_std[y_test==1, 1])

)

ymin = min(

min(X_train_std[y_train==0, 1]),

min(X_train_std[y_train==1, 1]),

min(X_test_std[y_test==0, 1]),

min(X_test_std[y_test==1, 1])

)

##### plot trainging and test Data

plt.xlim([math.floor(xmin), math.ceil(xmax)])

plt.ylim([math.floor(ymin), math.ceil(ymax)])

plt.scatter(X_train_std[y_train==0, 0], X_train_std[y_train==0, 1], c='blue', marker='x', label='train 0')

plt.scatter(X_train_std[y_train==1, 0], X_train_std[y_train==1, 1], c='red', marker='x', label='train 1')

plt.scatter(X_test_std[y_test==0, 0], X_test_std[y_test==0, 1], c='blue', marker='o', s=60, label='test 0')

plt.scatter(X_test_std[y_test==1, 0], X_test_std[y_test==1, 1], c='red', marker='o', s=60, label='test 1')

plt.legend(loc='upper left')

plt.title('Training Data and Test Data')

plt.xlabel('X1: Training Data and Test Data')

plt.ylabel('X2: Training Data and Test Data')

plt.savefig('Figure_2_Traing_Data_and_Test_Data.png')

plt.show()

plt.close()

########## Logistic Regression built by Standardized Training Data

#lr = LogisticRegression()

lr = LogisticRegression(C=c, penalty=pnlty)

lr.fit(X_train_std, y_train)

#check predict and score

#print(lr.predict(X_test_std))

#[1. 1. 0. 1. 1. 0. 1. 1. 0. 0. 1. 0. 1. 1. 0. 1. 1. 0. 1. 0.]

#print(y_test)

#[1. 1. 0. 1. 1. 1. 1. 0. 0. 0. 1. 0. 1. 1. 0. 1. 1. 0. 1. 0.]

#print(lr.predict(X_test_std))

#[1. 1. 0. 1. 1. 0. 1. 1. 0. 0. 1. 0. 1. 1. 0. 1. 1. 0. 1. 0.]

#[T T T T T F T F T T T T T T T T T T T T ]

#Number of T ( correct answers) = 18

#Number of F (incorrect answers) = 2

#18/(18+2) = 0.9

#print(lr.score(X_test_std, y_test))

#0.9

'''

A result of Logistic Regression is weights w0, w1, and w2 of a boundary line below:

w0+w1x+w2y=0

w0 is stored in intercept_ while w1 and w2 are included in coef_.

'''

#print (lr.intercept_)

#[-0.09150732]

#print (lr.coef_)

#[[1.99471124 2.32334603]]

w_0 = lr.intercept_[0]

w_1 = lr.coef_[0,0]

w_2 = lr.coef_[0,1]

# a boundary line

# w_0 + (w_1 * x) + (w_2 * y) = 0

# y = ((-w_1 * x) - w_0) / w_2

print("y = ((-w_1 * x) - w_0) / w_2")

print("y = (-w_1/w_2) * x - w_0/w_2")

print("y: x2")

print("x: x1")

print("w_0 = ", w_0)

print("w_1 = ", w_1)

print("w_2 = ", w_2)

print("(-w_1/w_2) = ", (-w_1/w_2))

print("(-w_0/w_2) = ", (-w_0/w_2))

'''

y = ((-w_1 * x) - w_0) / w_2

y = (-w_1/w_2) * x - w_0/w_2

y: x2

x: x1

w_0 = -0.09150731939635004

w_1 = 1.9947112354879184

w_2 = 2.3233460327656656

(-w_1/w_2) = -0.8585510756283915

(-w_0/w_2) = 0.03938600540162393

'''

# plotting a boundary line

#plt.plot([-2,2], map(lambda x: (-w_1 * x - w_0)/w_2, [-2,2]))

#plt.plot([-2,2], list(map(lambda x: (-w_1 * x - w_0)/w_2, [-2,2])))

plt.plot([math.floor(xmin) - 1, math.ceil(xmax) + 1], list(map(lambda x: (-w_1 * x - w_0)/w_2, [math.floor(xmin) - 1, math.ceil(xmax) + 1])))

# plotting Training Data and Test Data

plt.xlim([math.floor(xmin), math.ceil(xmax)])

plt.ylim([math.floor(ymin), math.ceil(ymax)])

plt.scatter(X_train_std[y_train==0, 0], X_train_std[y_train==0, 1], c='blue', marker='x', label='train 0')

plt.scatter(X_train_std[y_train==1, 0], X_train_std[y_train==1, 1], c='red', marker='x', label='train 1')

plt.scatter(X_test_std[y_test==0, 0], X_test_std[y_test==0, 1], c='blue', marker='o', s=60, label='test 0')

plt.scatter(X_test_std[y_test==1, 0], X_test_std[y_test==1, 1], c='red', marker='o', s=60, label='test 1')

plt.legend(loc='upper left')

plt.title('Training Data and Test Data plus a Boundary Line')

plt.xlabel('X1: Training Data and Test Data')

plt.ylabel('X2: Training Data and Test Data')

#plt.text(-2,-2, 'Boundary Line: x2 = (-w_1/w_2) * x1 - w_0/w_2 = ' + str(-w_1/w_2) + ' * x1 + ' + str(-w_0/w_2), size=10)

plt.text(math.floor(xmin) + (math.ceil(xmax) - math.floor(xmin)) * 0.05, math.floor(ymin) + (math.ceil(ymax) - math.floor(ymin)) * 0.20, 'Regularization: ' + str(pnlty), size=9)

plt.text(math.floor(xmin) + (math.ceil(xmax) - math.floor(xmin)) * 0.05, math.floor(ymin) + (math.ceil(ymax) - math.floor(ymin)) * 0.15, 'c = ' + str(c), size=9)

plt.text(math.floor(xmin) + (math.ceil(xmax) - math.floor(xmin)) * 0.05, math.floor(ymin) + (math.ceil(ymax) - math.floor(ymin)) * 0.10, 'Test score = ' + str(round(lr.score(X_test_std, y_test),3)*100) + '%', size=9)

plt.text(math.floor(xmin) + (math.ceil(xmax) - math.floor(xmin)) * 0.05, math.floor(ymin) + (math.ceil(ymax) - math.floor(ymin)) * 0.05, 'Boundary Line: x2 = ' + str(-w_1/w_2) + ' * x1 + ' + str(-w_0/w_2), size=9)

plt.savefig('Figure_3_Traing_Data_and_Test_Data_plus_Boundary_Line.png')

plt.show()

plt.close()

##### Confusion Matrix

cm = confusion_matrix(y_test, lr.predict(X_test_std))

print ("Confusion Matrix : \n", cm)

'''

Confusion Matrix :

[[ 7 1]

[ 0 12]]

'''

Out of 20 :

TruePostive + TrueNegative = 12 + 7

FalsePositive + FalseNegative = 1 + 0

[[TrueNegative(TN) FalsePositive(FP)]

[ FalseNegative(FN) TruePositive(TP)]]

Predicted Labels:

Negative Positive

Actual Results: Negative TrueNegative(TN) FalsePositive(FP)

Positive FalseNegative(FN) TruePositive(TP)

'''

#use 1, 2 as there are two independent variables x1 and x2

class_names=[1,2]

#fig, ax = plt.subplots()

fig, ax = plt.subplots(figsize=(6,5))

tick_marks = np.arange(len(class_names))

plt.xticks(tick_marks, class_names)

plt.yticks(tick_marks, class_names)

#sns.heatmap(pd.DataFrame(cm), annot=True, cmap="Blues" ,fmt='g')

sns.heatmap(pd.DataFrame(cm), annot=True, cmap="coolwarm", fmt='g')

ax.xaxis.set_label_position("top")

#plt.tight_layout()

plt.tight_layout(pad=3.00)

plt.title('Confusion Matrix (Test Data)')

plt.xlabel('Predicted Labels')

plt.ylabel('Actual Results')

#print("Accuracy:",metrics.accuracy_score(y_test, y_pred))

plt.savefig("Figure_4_Confusion_Matrix_Test_Data.png")

plt.show()

plt.close()

########## Logistic Regression built by Standardized Training Data (+ Regularization parameter C)

'''

The larger the C, the weaker regularization is going to be.

C is 1.0 by default. We try 1, 10, 100, 1000 here.

'''

fig, axs = plt.subplots(2, 2, sharex=True, sharey=True)

plt.xlim([math.floor(xmin), math.ceil(xmax)])

plt.ylim([math.floor(ymin), math.ceil(ymax)])

plt.subplots_adjust(wspace=0.1, hspace=0.6)

c_params = [1.0, 10.0, 100.0, 1000.0]

#print(c_params)

#[1.0, 10.0, 100.0, 1000.0]

#print(type(c_params))

#<class 'list'>

#print(enumerate(c_params))

#<enumerate object at 0x127bec500>

for i, c in enumerate(c_params):

#print(i, c)

#lr = LogisticRegression(C=c)

lr = LogisticRegression(C=c, penalty=pnlty)

lr.fit(X_train_std, y_train)

w_0 = lr.intercept_[0]

w_1 = lr.coef_[0,0]

w_2 = lr.coef_[0,1]

score = lr.score(X_test_std, y_test)

#print(i/2, i%2)

#print(math.floor(i/2), i%2)

#####axs[i/2, i%2].set_title('C=' + str(c))

axs[math.floor(i/2), i%2].set_title('C=' + str(c))

#####axs[i/2, i%2].plot([-2,2], map(lambda x: (-w_1 * x - w_0)/w_2, [-2,2]))

axs[math.floor(i/2), i%2].plot([math.floor(xmin)-1, math.ceil(xmax)+1], list(map(lambda x: (-w_1 * x - w_0)/w_2, [math.floor(xmin)-1, math.ceil(xmax)+1])))

#####axs[i/2, i%2].scatter(X_train_std[y_train==0, 0], X_train_std[y_train==0, 1], c='red', marker='x', label='train 0')

#axs[math.floor(i/2), i%2].scatter(X_train_std[y_train==0, 0], X_train_std[y_train==0, 1], c='red', marker='x', label='train 0')

axs[math.floor(i/2), i%2].scatter(X_train_std[y_train==0, 0], X_train_std[y_train==0, 1], c='blue', marker='x', label='train 0')

#####axs[i/2, i%2].scatter(X_train_std[y_train==1, 0], X_train_std[y_train==1, 1], c='blue', marker='x', label='train 1')

#axs[math.floor(i/2), i%2].scatter(X_train_std[y_train==1, 0], X_train_std[y_train==1, 1], c='blue', marker='x', label='train 1')

axs[math.floor(i/2), i%2].scatter(X_train_std[y_train==1, 0], X_train_std[y_train==1, 1], c='red', marker='x', label='train 1')

#####axs[i/2, i%2].scatter(X_test_std[y_test==0, 0], X_test_std[y_test==0, 1], c='red', marker='o', s=60, label='test 0')

#axs[math.floor(i/2), i%2].scatter(X_test_std[y_test==0, 0], X_test_std[y_test==0, 1], c='red', marker='o', s=60, label='test 0')

axs[math.floor(i/2), i%2].scatter(X_test_std[y_test==0, 0], X_test_std[y_test==0, 1], c='blue', marker='o', s=60, label='test 0')

#####axs[i/2, i%2].scatter(X_test_std[y_test==1, 0], X_test_std[y_test==1, 1], c='blue', marker='o', s=60, label='test 1')

#axs[math.floor(i/2), i%2].scatter(X_test_std[y_test==1, 0], X_test_std[y_test==1, 1], c='blue', marker='o', s=60, label='test 1')

axs[math.floor(i/2), i%2].scatter(X_test_std[y_test==1, 0], X_test_std[y_test==1, 1], c='red', marker='o', s=60, label='test 1')

if (i < 2):

#####axs[i/2, i%2].text(0,-2.7, 'score ' + str(round(score,3)*100) + '%', size=13)

axs[math.floor(i/2), i%2].text(math.floor(xmin) + (math.ceil(xmax) - math.floor(xmin)) * 0.10, math.ceil(ymax) - (math.ceil(ymax) - math.floor(ymin)) * 0.10, 'score ' + str(round(score,3)*100) + '%', size=10)

else:

#####axs[i/2, i%2].text(0,-3.3, 'score ' + str(round(score,3)*100) + '%', size=13)

plt.savefig('Figure_5_Traing_Data_and_Test_Data_plus_Boundary_Line_for_various_Cs.png')

plt.show()

plt.close()