| # Install on Terminal of MacOS # 1. NumPy #pip3 install -U numpy # 2. scikit-learn (sklearn) #pip3 install -U scikit-learn # 3.statsmodels #pip3 install -U statsmodels #4. matplotlib #pip3 install -U matplotlib |
1_MacOS_Terminal.txt
| ########## Run Terminal on MacOS and execute ### TO UPDATE cd "YOUR_WORKING_DIRECTORY" |
Python files
| ########## Linear Regression in Python ########## # # # Reference: # # Linear Regression in Python # by Mirko Stojiljkovic # https://realpython.com/linear-regression-in-python/ ##### Regression ### What Is Regression? #y: The dependent features are called the dependent variables, outputs, or responses. #x = (x1, x2, ..., xr) where r is the number of inputs: The independent features are called the independent variables, inputs, or predictors. # #Regression problems usually have one continuous and unbounded dependent variable. The inputs, however, can be continuous, discrete, or even categorical data such as gender, nationality, brand, and so on. ### When Do You Need Regression? ##### Linear Regression ### Problem Formulation # # dependent variable (actual response) ๐ฆ # independent variables ๐ฑ = (๐ฅ₁, …, ๐ฅแตฃ), where ๐ is the number of predictors # # ๐ฆ = ๐ฝ₀ + ๐ฝ₁๐ฅ₁ + ⋯ + ๐ฝแตฃ๐ฅแตฃ + ๐. # This equation is the regression equation. # # ๐ฝ₀, ๐ฝ₁, …, ๐ฝแตฃ are the regression coefficients, and ๐ is the random error. # estimated regression function ๐(๐ฑ) = ๐₀ + ๐₁๐ฅ₁ + ⋯ + ๐แตฃ๐ฅแตฃ # predicted weights: ๐₀, ๐₁, …, ๐แตฃ # The estimated or predicted response, ๐(๐ฑแตข), for each observation ๐ = 1, …, ๐, # should be as close as possible to the corresponding actual response ๐ฆแตข. # The differences ๐ฆแตข - ๐(๐ฑแตข) for all observations ๐ = 1, …, ๐, are called the residuals. # Regression is about determining the best predicted weights, that is the weights corresponding to the smallest residuals. #To get the best weights, you usually minimize the sum of squared residuals (SSR) # for all observations ๐ = 1, …, ๐: SSR = ฮฃแตข(๐ฆแตข - ๐(๐ฑแตข))². # This approach is called the method of ordinary least squares. ### Regression Performance # The coefficient of determination, denoted as ๐ ², tells you which amount of variation in ๐ฆ can be explained by the dependence on ๐ฑ using the particular regression model. Larger ๐ ² indicates a better fit and means that the model can better explain the variation of the output with different inputs. # # The value ๐ ² = 1 corresponds to SSR = 0, that is to the perfect fit since the values of predicted and actual responses fit completely to each other. ### Simple (or Single-Variate) Linear Regression #The residuals (vertical dashed gray lines) can be calculated as ๐ฆแตข - ๐(๐ฑแตข) = ๐ฆแตข - ๐₀ - ๐₁๐ฅแตข for ๐ = 1, …, ๐. ### Multiple (or Multivariate) Linear Regression #The estimated regression function is ๐(๐ฅ₁, …, ๐ฅแตฃ) = ๐₀ + ๐₁๐ฅ₁ + ⋯ +๐แตฃ๐ฅแตฃ, and there are ๐ + 1 weights to be determined when the number of inputs is ๐. ### Polynomial Regression # # a generalized case of linear regression # In addition to linear terms like ๐₁๐ฅ₁, your regression function ๐ can include non-linear terms such as ๐₂๐ฅ₁², ๐₃๐ฅ₁³, or even ๐₄๐ฅ₁๐ฅ₂, ๐₅๐ฅ₁²๐ฅ₂, and so on. # Now, remember that you want to calculate ๐₀, ๐₁, and ๐₂, which minimize SSR. These are your unknowns! ### Underfitting and Overfitting ##### Implementing Linear Regression in Python ### Python Packages for Linear Regression # 1. NumPy # 2. scikit-learn (sklearn) # 3.statsmodels ###Simple Linear Regression With scikit-learn ##Step 1: Import packages and classes import numpy as np from sklearn.linear_model import LinearRegression ##Step 2: Provide data # #arrays # inputs (regressors, ๐ฅ) # output (predictor, ๐ฆ) # x = np.array([5, 15, 25, 35, 45, 55]).reshape((-1, 1)) y = np.array([5, 20, 14, 32, 22, 38]) #You should call .reshape() on x because this array is required to be two-dimensional, or to be more precise, to have one column and as many rows as necessary. That’s exactly what the argument (-1, 1) of .reshape() specifies. print(x) #[[ 5] # [15] # [25] # [35] # [45] # [55]] #print(x.shape) #(6, 1) print(y) #[ 5 20 14 32 22 38] #print(y.shape) #(6,) ##Step 3: Create a model and fit it #model = LinearRegression() # optional parameters to LinearRegression: # # - fit_intercept is a Boolean (True by default) that decides whether to calculate the intercept ๐₀ (True) or consider it equal to zero (False). # - normalize is a Boolean (False by default) that decides whether to normalize the input variables (True) or not (False). # - copy_X is a Boolean (True by default) that decides whether to copy (True) or overwrite the input variables (False). # - n_jobs is an integer or None (default) and represents the number of jobs used in parallel computation. None usually means one job and -1 to use all processors. #model.fit(x, y) #With .fit(), you calculate the optimal values of the weights ๐₀ and ๐₁, using the existing input and output (x and y) as the arguments. model = LinearRegression().fit(x, y) #This statement does the same thing as the previous two. # #model = LinearRegression() #model.fit(x, y) ##Step 4: Get results #.score() #coefficient of determination (๐ ²) # ๐ ² = model.score(predictor x, regressor y) r_sq = model.score(x, y) print('coefficient of determination:', r_sq) #coefficient of determination: 0.7158756137479542 #The attributes of model are #.intercept_, which represents the coefficient, ๐₀ and #.coef_, which represents ๐₁: print('intercept:', model.intercept_) #intercept: 5.633333333333329 #.intercept_ is a scalar, print('slope:', model.coef_) #slope: [0.54] #.coef_ is an array #You should notice that you can provide y as a two-dimensional array as well. In this case, you’ll get a similar result. This is how it might look: new_model = LinearRegression().fit(x, y.reshape((-1, 1))) print('intercept:', new_model.intercept_) #intercept: [5.63333333] # print('slope:', new_model.coef_) #slope: [[0.54]] # #.intercept_ is a one-dimensional array with the single element ๐₀, and .coef_ is a two-dimensional array with the single element ๐₁. ##Step 5: Predict response y_pred = model.predict(x) print('predicted response:', y_pred, sep='\n') #predicted response: #[ 8.33333333 13.73333333 19.13333333 24.53333333 29.93333333 35.33333333] # #print(y) #[ 5 20 14 32 22 38] #This is a nearly identical way to predict the response: y_pred = model.intercept_ + model.coef_ * x print('predicted response:', y_pred, sep='\n') #predicted response: #[[ 8.33333333] # [13.73333333] # [19.13333333] # [24.53333333] # [29.93333333] # [35.33333333]] #The output here differs from the previous example only in dimensions. The predicted response is now a two-dimensional array, while in the previous case, it had one dimension. #If you reduce the number of dimensions of x to one, these two approaches will yield the same result. You can do this by replacing x with x.reshape(-1), x.flatten(), or x.ravel() when multiplying it with model.coef_. # #model2 = LinearRegression().fit(x, y) #new_model2 = LinearRegression().fit(x, y.reshape((-1, 1))) #r_sq2 = model2.score(x, y) #y_pred2 = model.predict(x) #y_pred2 = model.predict(x.reshape(-1)) # #y_pred2 = model.intercept_ + model.coef_ * x.reshape(-1) #print('predicted response:', y_pred2, sep='\n') #predicted response: #[ 8.33333333 13.73333333 19.13333333 24.53333333 29.93333333 35.33333333] #In practice, regression models are often applied for forecasts. This means that you can use fitted models to calculate the outputs based on some other, new inputs: x_new = np.arange(5).reshape((-1, 1)) print(x_new) #[[0] # [1] # [2] # [3] # [4]] y_new = model.predict(x_new) print(y_new) #[5.63333333 6.17333333 6.71333333 7.25333333 7.79333333] ### #X-Y Plots (scatter plot) # import matplotlib.pyplot as plt # #x = np.arange(21) #y = 5 + 2 * x + 2 * np.random.randn(21) #slope, intercept, r, *__ = scipy.stats.linregress(x, y) #line = f'Regression line: y={intercept:.2f}+{slope:.2f}x, r={r:.2f}' # #matplotlib.axes.Axes.plot #.plot() # # fig, ax = plt.subplots() # # #Training Data ax.plot(x, y, linewidth=0, marker='s', label='y') ax.plot(x, y_pred, label='y_pred') #ax.plot(x, y_pred, label=line) #ax.plot(x, intercept + slope * x, label=line) # # #Test Data ax.plot(x_new, y_new, label='y_new') # # ax.set_xlabel('x') ax.set_ylabel('y') ax.legend(facecolor='white') plt.savefig("Figure_Simple_Linear_Regression_With_scikit-learn.png") # added to save a figure plt.show() # ### ###Multiple Linear Regression With scikit-learn ##Steps 1 and 2: Import packages and classes, and provide data import numpy as np from sklearn.linear_model import LinearRegression x = [[0, 1], [5, 1], [15, 2], [25, 5], [35, 11], [45, 15], [55, 34], [60, 35]] y = [4, 5, 20, 14, 32, 22, 38, 43] x, y = np.array(x), np.array(y) print(x) #[[ 0 1] # [ 5 1] # [15 2] # [25 5] # [35 11] # [45 15] # [55 34] # [60 35]] print(y) #[ 4 5 20 14 32 22 38 43] #In multiple linear regression, x is a two-dimensional array with at least two columns, while y is usually a one-dimensional array. This is a simple example of multiple linear regression, and x has exactly two columns. ##Step 3: Create a model and fit it model = LinearRegression().fit(x, y) ##Step 4: Get results r_sq = model.score(x, y) print('coefficient of determination:', r_sq) #coefficient of determination: 0.8615939258756776 print('intercept:', model.intercept_) #intercept: 5.52257927519819 print('slope:', model.coef_) #slope: [0.44706965 0.25502548] ##Step 5: Predict response y_pred = model.predict(x) print('predicted response:', y_pred, sep='\n') #predicted response: #[ 5.77760476 8.012953 12.73867497 17.9744479 23.97529728 29.4660957 # 38.78227633 41.27265006] y_pred = model.intercept_ + np.sum(model.coef_ * x, axis=1) print('predicted response:', y_pred, sep='\n') #You can apply this model to new data as well: x_new = np.arange(10).reshape((-1, 2)) print(x_new) #[[0 1] # [2 3] # [4 5] # [6 7] # [8 9]] y_new = model.predict(x_new) print(y_new) #[ 5.77760476 7.18179502 8.58598528 9.99017554 11.3943658 ] ###Polynomial Regression With scikit-learn #Implementing polynomial regression with scikit-learn is very similar to linear regression. There is only one extra step: you need to transform the array of inputs to include non-linear terms such as ๐ฅ². ##Step 1: Import packages and classes import numpy as np from sklearn.linear_model import LinearRegression from sklearn.preprocessing import PolynomialFeatures ##Step 2a: Provide data x = np.array([5, 15, 25, 35, 45, 55]).reshape((-1, 1)) y = np.array([15, 11, 2, 8, 25, 32]) #Keep in mind that you need the input to be a two-dimensional array. That’s why .reshape() is used. #print(x) #[[ 5] # [15] # [25] # [35] # [45] # [55]] ##Step 2b: Transform input data #transformer = PolynomialFeatures(degree=2, include_bias=False) # # - degree is an integer (2 by default) that represents the degree of the polynomial regression function. # - interaction_only is a Boolean (False by default) that decides whether to include only interaction features (True) or all features (False). # - include_bias is a Boolean (True by default) that decides whether to include the bias (intercept) column of ones (True) or not (False). # #transformer.fit(x) # #x_ = transformer.transform(x) #It takes the input array as the argument and returns the modified array. # #You can also use .fit_transform() to replace the three previous statements with only one: x_ = PolynomialFeatures(degree=2, include_bias=False).fit_transform(x) #modified array print(x_) #[[ 5. 25.] # [ 15. 225.] # [ 25. 625.] # [ 35. 1225.] # [ 45. 2025.] # [ 55. 3025.]] #The modified input array contains two columns: one with the original inputs and the other with their squares. #print(PolynomialFeatures(degree=3, include_bias=False).fit_transform(x)) #[[5.00000e+00 2.50000e+01 1.25000e+02] # [1.50000e+01 2.25000e+02 3.37500e+03] # [2.50000e+01 6.25000e+02 1.56250e+04] # [3.50000e+01 1.22500e+03 4.28750e+04] # [4.50000e+01 2.02500e+03 9.11250e+04] # [5.50000e+01 3.02500e+03 1.66375e+05]] # #print(5**3) #125 (=1.25000e+02) ##Step 3: Create a model and fit it model = LinearRegression().fit(x_, y) #You should keep in mind that the first argument of .fit() is the modified input array x_ and not the original x. #Step 4: Get results r_sq = model.score(x_, y) print('coefficient of determination:', r_sq) #coefficient of determination: 0.8908516262498564 print('intercept:', model.intercept_) #intercept: 21.372321428571425 print('coefficients:', model.coef_) #coefficients: [-1.32357143 0.02839286] #include_bias=True instead of include_bias=False x_ = PolynomialFeatures(degree=2, include_bias=True).fit_transform(x) # The additional leftmost column containing only ones. # This column corresponds to the intercept. print(x_) #[[1.000e+00 5.000e+00 2.500e+01] # [1.000e+00 1.500e+01 2.250e+02] # [1.000e+00 2.500e+01 6.250e+02] # [1.000e+00 3.500e+01 1.225e+03] # [1.000e+00 4.500e+01 2.025e+03] # [1.000e+00 5.500e+01 3.025e+03]] # #The first column of x_ contains ones, the second has the values of x, while the third holds the squares of x. #The intercept is already included with the leftmost column of ones, and you don’t need to include it again when creating the instance of LinearRegression. Thus, you can provide fit_intercept=False. This is how the next statement looks: model = LinearRegression(fit_intercept=False).fit(x_, y) r_sq = model.score(x_, y) print('coefficient of determination:', r_sq) #coefficient of determination: 0.8908516262498565 print('intercept:', model.intercept_) #intercept: 0.0 print('coefficients:', model.coef_) #coefficients: [21.37232143 -1.32357143 0.02839286] #You see that now .intercept_ is zero, but .coef_ actually contains ๐₀ as its first element. Everything else is the same. ##Step 5: Predict response y_pred = model.predict(x_) print('predicted response:', y_pred, sep='\n') #predicted response: #[15.46428571 7.90714286 6.02857143 9.82857143 19.30714286 34.46428571] #You can apply the identical procedure if you have several input variables. You’ll have an input array with more than one column, but everything else is the same. Here is an example: # Step 1: Import packages import numpy as np from sklearn.linear_model import LinearRegression from sklearn.preprocessing import PolynomialFeatures # Step 2a: Provide data x = [[0, 1], [5, 1], [15, 2], [25, 5], [35, 11], [45, 15], [55, 34], [60, 35]] y = [4, 5, 20, 14, 32, 22, 38, 43] x, y = np.array(x), np.array(y) # Step 2b: Transform input data x_ = PolynomialFeatures(degree=2, include_bias=False).fit_transform(x) # Step 3: Create a model and fit it model = LinearRegression().fit(x_, y) # Step 4: Get results r_sq = model.score(x_, y) intercept, coefficients = model.intercept_, model.coef_ # Step 5: Predict y_pred = model.predict(x_) #This regression example yields the following results and predictions: # print('coefficient of determination:', r_sq) #coefficient of determination: 0.9453701449127822 print('intercept:', intercept) #intercept: 0.8430556452395734 print('coefficients:', coefficients, sep='\n') #coefficients: #[ 2.44828275 0.16160353 -0.15259677 0.47928683 -0.4641851 ] print('predicted response:', y_pred, sep='\n') #predicted response: #[ 0.54047408 11.36340283 16.07809622 15.79139 29.73858619 23.50834636 # 39.05631386 41.92339046] #In this case, there are six regression coefficients (including the intercept), as shown in the estimated regression function ๐(๐ฅ₁, ๐ฅ₂) = ๐₀ + ๐₁๐ฅ₁ + ๐₂๐ฅ₂ + ๐₃๐ฅ₁² + ๐₄๐ฅ₁๐ฅ₂ + ๐₅๐ฅ₂². ###Advanced Linear Regression With statsmodels ##Step 1: Import packages import numpy as np import statsmodels.api as sm ##Step 2: Provide data and transform inputs x = [[0, 1], [5, 1], [15, 2], [25, 5], [35, 11], [45, 15], [55, 34], [60, 35]] y = [4, 5, 20, 14, 32, 22, 38, 43] x, y = np.array(x), np.array(y) #You need to add the column of ones to the inputs if you want statsmodels to calculate the intercept ๐₀. It doesn’t takes ๐₀ into account by default. This is just one function call: # x = sm.add_constant(x) print(x) #[[ 1. 0. 1.] # [ 1. 5. 1.] # [ 1. 15. 2.] # [ 1. 25. 5.] # [ 1. 35. 11.] # [ 1. 45. 15.] # [ 1. 55. 34.] # [ 1. 60. 35.]] print(y) #[ 4 5 20 14 32 22 38 43] ##Step 3: Create a model and fit it #The regression model based on ordinary least squares is an instance of the class statsmodels.regression.linear_model.OLS. This is how you can obtain one: model = sm.OLS(y, x) results = model.fit() ##Step 4: Get results print(results.summary()) #In this particular case, you might obtain the warning related to kurtosistest. This is due to the small number of observations provided. #1. .rsquared holds ๐ ². print('coefficient of determination:', results.rsquared) #coefficient of determination: 0.8615939258756777 #2. .rsquared_adj represents adjusted ๐ ² (๐ ² corrected according to the number of input features). print('adjusted coefficient of determination:', results.rsquared_adj) #adjusted coefficient of determination: 0.8062314962259488 #3. params refers the array with ๐₀, ๐₁, and ๐₂ respectively. print('regression coefficients:', results.params) #regression coefficients: [5.52257928 0.44706965 0.25502548] ## Step 5: Predict response print('predicted response:', results.fittedvalues, sep='\n') #predicted response: #[ 5.77760476 8.012953 12.73867497 17.9744479 23.97529728 29.4660957 # 38.78227633 41.27265006] print('predicted response:', results.predict(x), sep='\n') #predicted response: #[ 5.77760476 8.012953 12.73867497 17.9744479 23.97529728 29.4660957 # 38.78227633 41.27265006] x_new = sm.add_constant(np.arange(10).reshape((-1, 2))) print(x_new) #[[1. 0. 1.] # [1. 2. 3.] # [1. 4. 5.] # [1. 6. 7.] # [1. 8. 9.]] y_new = results.predict(x_new) print(y_new) #[ 5.77760476 7.18179502 8.58598528 9.99017554 11.3943658 ] #####Beyond Linear Regression #Linear regression is sometimes not appropriate, especially for non-linear models of high complexity. #Fortunately, there are other regression techniques suitable for the cases where linear regression doesn’t work well. Some of them are support vector machines, decision trees, random forest, and neural networks. #####Conclusion |
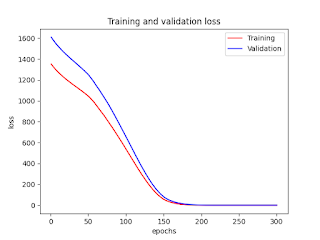
Figures
Figure_Simple_Linear_Regression_With_scikit-learn.png
Reference
by Mirko Stojiljkovic
https://realpython.com/linear-regression-in-python/
Thanks, priyanka, for your encouraging comment!
ReplyDelete