| # Install on Terminal of MacOS #1. matplotlib #pip3 install -U matplotlib #2. NumPy #pip3 install -U numpy #3. scikit-learn (sklearn) #pip3 install -U scikit-learn #4. sympy #pip3 install -U sympy #5. IPython #pip3 install -U IPython #6. pandas #pip3 install -U pandas |
1_MacOS_Terminal.txt
| ########## Run Terminal on MacOS and execute ### TO UPDATE cd "YOUR_WORKING_DIRECTORY" python3 prs01.py 5 training.csv test.csv |
Data files
training.csv
x_training,y_training 9,51 28,80 38,112 58,294 88,286 98,110 108,59 118,70 128,56 138,70 148,104 158,59 168,59 178,72 188,87 198,99 208,64 218,60 228,74 238,151 278,157 288,57 298,83 |
test.csv
| x_test,y_test 9,56 98,99 148,114 198,89 278,173 |
Python files
| ########## Polynomial Regression (Simple) ########## import numpy as np import matplotlib.pyplot as plt from sklearn.metrics import r2_score import sys import os import sympy as sym from sympy.plotting import plot #from Python.display import display #import display from IPython.display import display import pandas as pd ### Training Data #x_training = [9, 28, 38, 58, 88, 98, 108, 118, 128, 138, 148, 158, 168, 178, 188, 198, 208, 218, 228, 238, 278, 288, 298] #y_training = [51, 80, 112, 294, 286, 110, 59, 70, 56, 70, 104, 59, 59, 72, 87, 99, 64, 60, 74, 151, 157, 57, 83] trainingcsv = sys.argv[2] #tmp = pd.read_csv("training.csv", index_col=0) #tmp_training = pd.read_csv("training.csv") tmp_training = pd.read_csv(trainingcsv) print(tmp_training) # #len(tmp) #23 #len(tmp.columns) #2 # #tmpx = tmp.iloc[:,0] #tmpy = tmp.iloc[:,1] # x_training = tmp_training.iloc[:,0].values.tolist() y_training = tmp_training.iloc[:,1].values.tolist() plt.scatter(x_training, y_training) plt.grid() ### Test Data #x_test = [9, 98, 148, 198, 278] #y_test = [56, 99, 114, 89, 173] testcsv = sys.argv[3] #tmp_test = pd.read_csv("test.csv") tmp_test = pd.read_csv(testcsv) x_test = tmp_test.iloc[:,0].values.tolist() y_test = tmp_test.iloc[:,1].values.tolist() plt.scatter(x_test, y_test, label='Test Data') # equally spaced, 100 points from min(x_training) to max(x_training) for ponlynominal regression models x_latent = np.linspace(min(x_training), max(x_training), 100) #deg = sys.argv[1] deg = int(sys.argv[1]) #least-squares method (Degree of the polynomial fitting: n) #LSM (Deg: n) cf = ["LSM (Deg: " + str(deg) + ")", lambda x, y: np.polyfit(x, y, deg)] sym.init_printing(use_unicode=True) x, y = sym.symbols("x y") #for method_name, method in [cf1, cf2, cf3, cf4, cf5, cf6, cf7, cf8, cf9]: for method_name, method in [cf]: print(method_name) ### calculating coefficients coefficients = method(x_training, y_training) ### sympy to show an equation expr = 0 for index, coefficient in enumerate(coefficients): expr += coefficient * x ** (len(coefficients) - index - 1) display(sym.Eq(y, expr)) ###R2 fitted_curve = np.poly1d(method(x_training, y_training)) #print(fitted_curve) r2 = r2_score(y_training, fitted_curve(x_training)) print(r2_score(y_training, fitted_curve(x_training))) #0.14298353303806732 ### data plotting and drawing a fitted model fitted_curve = np.poly1d(method(x_training, y_training))(x_latent) # plt.scatter(x_training, y_training, label="Training Data") plt.plot(x_latent, fitted_curve, c="red", label="Polynominal Regession Fitting with Training Data") plt.grid() #plt.legend() plt.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=0, fontsize=8) plt.text(min(x_training),max(y_training)*0.85,sym.Eq(y, expr),fontsize=6) plt.text(min(x_training),max(y_training)*0.80,"R2 = " + str(r2),fontsize=6) plt.savefig("Figure_deg_" + str(deg) + ".png") # added to save a figure plt.show() ''' imageFile = sys.argv[2] #imageFile = "img.jpg" #Get working directory workPath = os. getcwd() #print(workPath) imagePath = workPath + "/" + imageFile #print(imagePath) ''' |
Figures

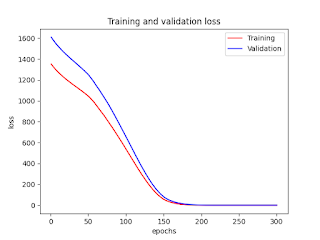

No comments:
Post a Comment